- Learn a language for 15 minutes a day and make rapid progress.
- Permanently retain vocabulary and expressions with the globally acclaimed SuperMemo intelligent repetition method.
- Gain access to 25 languages and nearly 300 courses.
- Develop your speaking skills by practicing real conversations in MemoChat with AI technology.
- Use the app on any number of devices, online or offline.
Make yourself a gift!
1 year of learning 20% off
Premium subscription 12 months
Use code: PREMIUMX20
Which language would you like to learn?
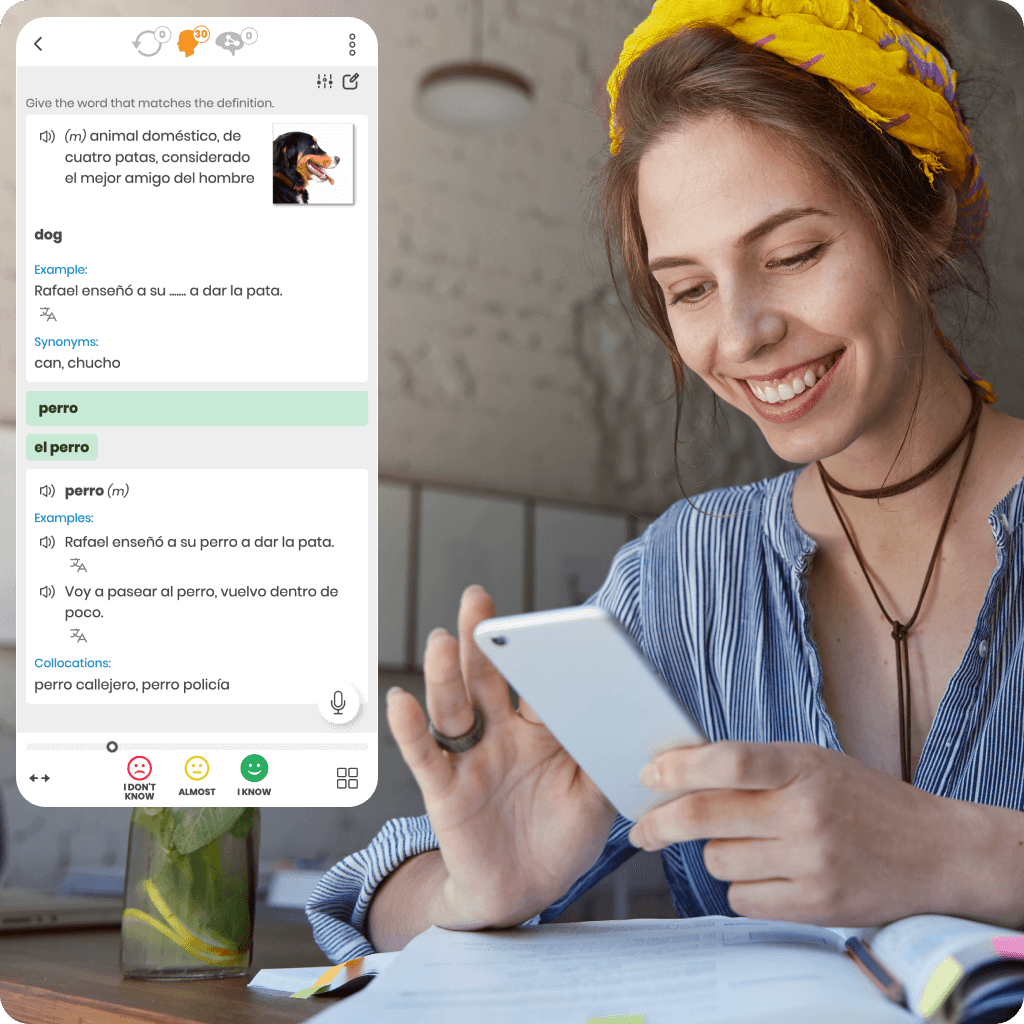
We were the first to introduce the intelligent repetition system to support effective online learning. Our unique research and development make us leaders in this technology.
Every online language course we offer is based on a proprietary algorithm that precisely determines the ideal moment for reviews. This ensures you learn faster, more effectively, and retain knowledge for longer.
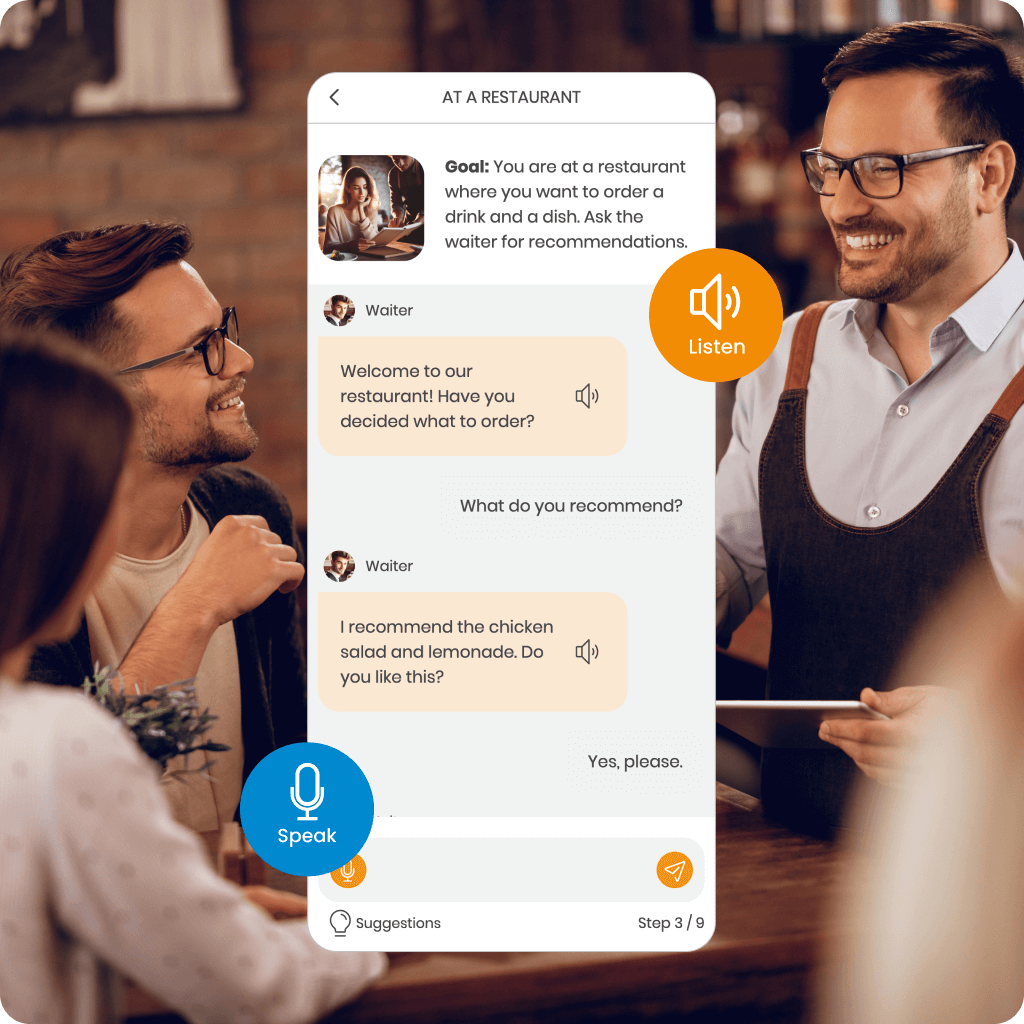
Discover MemoChat – interactive dialogues in SuperMemo powered by AI, offering a variety of conversation topics and the ability to propose your own. MemoChat provides response suggestions, instant translations, and error corrections, while newly learned words can easily be added to your courses, creating personalized study materials.
With the help of the AI Assistant, you will understand grammar, translate unfamiliar words, and learn how to use them correctly in context, significantly accelerating your progress.
Additionally, the MemoTranslator instantly translates words and sentences, which you can also add to your courses to make your learning even more effective.
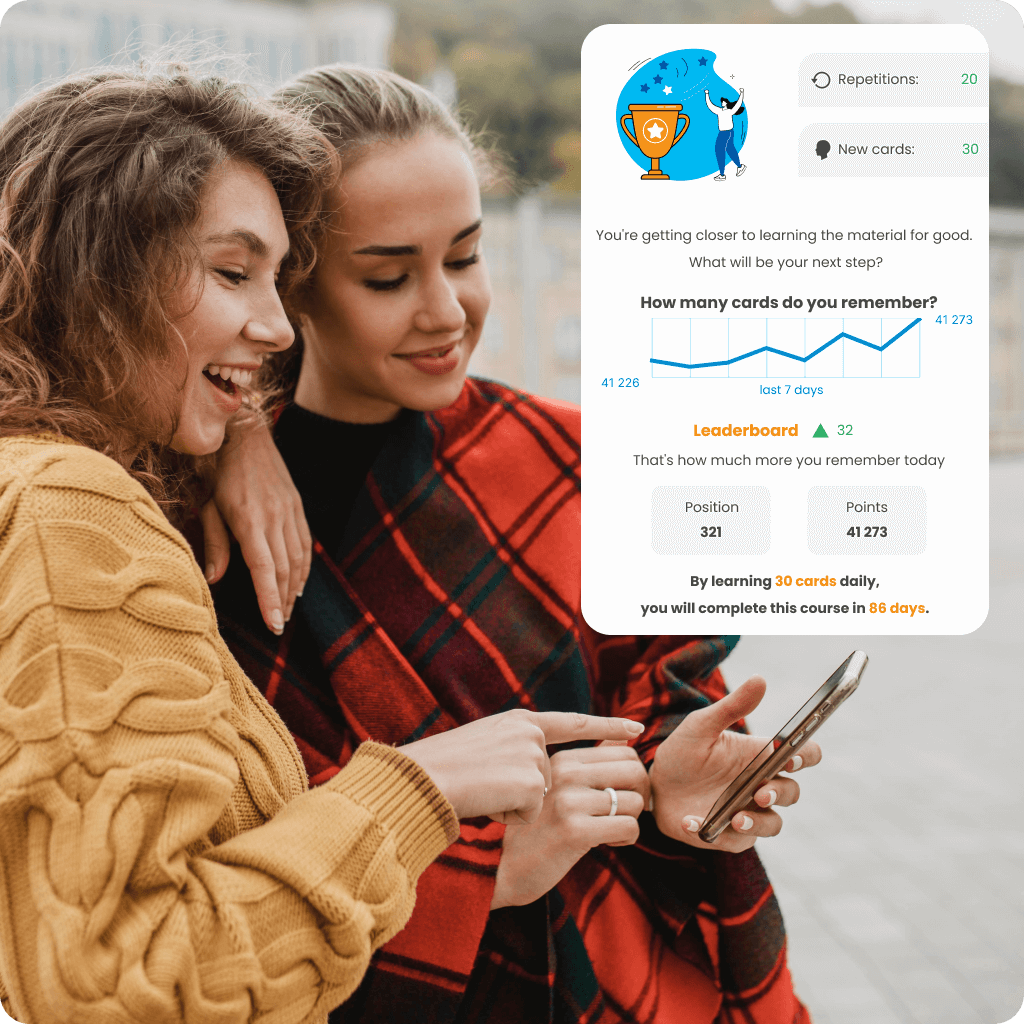
Adjust your language learning pace to suit your needs and available time with a personalized learning plan. Track your progress in real-time with statistics, check how much you’ve already mastered, and see how you rank among other users in the ranking. Choose a course that not only motivates you to act but also helps you achieve your goals effectively.

Explore a variety of courses that develop vocabulary and grammar at every proficiency level. Gain confidence in speaking with the speech recognition feature and interactive dialogues. Improve your reading comprehension skills and perfect your spelling.


