Dr Piotr Wozniak, June 2018
Contents
- Introduction
- 1985: Birth of SuperMemo
- 1986: First steps of SuperMemo
- 1987: SuperMemo 1.0 for DOS
- 1988: Two component of memory
- 1989: SuperMemo adapts to user memory
- 1990: Universal formula for memory
- 1991: Employing forgetting curves
- 1994: Exponential nature of forgetting
- 1995: Hypermedia SuperMemo
- 1997: Employing neural networks
- 1999: Choosing the name: “spaced repetition”
- 2005: Stability increase function
- 2014: Algorithm SM-17
- Exponential adoption of spaced repetition
- Summary of memory research
- The anatomy of failure and success
Introduction
True history
The popular history of spaced repetition is full of myths and falsehoods. This text is to tell you the true story. The problem with spaced repetition is that it became too popular for its own effective replication. Like a fast mutating virus it keeps jumping from application to application, and tells its own story while accumulating errors on the way.
Who invented spaced repetition?
This is the story of how I solved the problem of forgetting. I figured out how to learn efficiently. Modesty is a waste of time, therefore I will add that I think I actually know how to significantly amplify human intelligence. In short: memory underlies knowledge which underlies intelligence. If we can control what we store in memory and what we forget, we can control our problem solving capacity. In a very similar way, we can also amplify artificial intelligence. Its a great relief to be able to type in those proud words after many years of a gag order imposed by commercial considerations.
Back in the early 1990s, I thought I knew how to turn education systems around the world upside down and make them work for all students. However, any major change requires a cultural paradigm shift. It is not enough for a poor student from a poor communist country to announce the potential for a change. I did that, in my Master’s Thesis, but I found little interest in my ideas. Even my own family was dismissive. Luckily, I met a few smart friends at my university who declared they would use my ideas to set up a business. Like Microsoft changed the world of personal computing, we would change the way people learn. We owned a powerful learning tool: SuperMemo. However, for SuperMemo to conquer the world it had to ditch its roots for a while. To convince others, SuperMemo had to be a product of pure science. It could not have just been an idea conceived by a humble student.
To root SuperMemo in science, we made a major effort to publish our ideas in a peer-review journal, adopted a little known scientific term of ” spaced repetition ” and set our learning technology in a context of learning theory and the history of research in psychology. I am very skeptical of schools, certificates, and titles. However, I still went as far as to earn a PhD in economics of learning, to add respectability to my words.
Today, when spaced repetition is finally showing up in hundreds of respectable learning tools, applications, and services, we can finally stake the claim and plant the flag at the summit. Usership is going into hundreds of millions.
If you read SuperMemopedia here you may conclude that “Nobody should ever take credit for discovering spaced repetition”. I beg to disagree. In this text I will claim the full credit for the discovery, and some solid credit for the dissemination of the idea. My contribution to the latter is waning thanks to the power of the idea itself and a growing circle of people involved in the concept (well beyond our company).
Perpetuating myths
It is Krzysztof Biedalak (CEO), who got least patience with fake news in reference to spaced repetition. I will then credit this particular text and the effort in mythbusting to his resolution to keep the history straight. SuperMemo for DOS was born 30 years ago (1987). Let’s pay some tribute.
If you believe that Ebbinghaus invented spaced repetition in 1885, I apologize. When compiling the history of SuperMemo, we put the name of the venerable German psychologist at the top of the chronological list and the myth was born. Ebbinghaus never worked over spaced repetition.
Writing about history of spaced repetition is not easy. Each time we do it, we generate more myths through distortions and misunderstandings. Let’s then make it clear and emphatic. There has been a great deal of memory research before SuperMemo. However, each time I give prolific credit, keep in mind the words of Biedalak:
If SuperMemo is a space shuttle, we need to acknowledge prior work done on bicycles. In the meantime, our competition is busy trying to replicate our shuttle, but the efforts are reminiscent of the Soviet Buran program. Buran has at least made one space flight. It was unmanned
This texts is to put the facts straight, and openly disclose the early steps of spaced repetition. This is a fun foray into the past that brings me a particular delight with the sense of “mission accomplished”. Now that we can call our effort a global success, there is no need to make it more respectable than it really is. No need to make it more scientific, more historic, or more certified.
Spaced repetition is here and it here to stay. We did it!
Credits
The list of contributors to the idea of spaced repetition is too long to include in this short article. Some names do not show up because I simply run out of allocated time to describe their efforts. Dr Phil Pavlik got probably most fresh ideas in the field. An array of memory researchers investigate the impact of spacing on memory. Duolingo and Quizlet are leading competitors with a powerful impact on the good promotion of the idea. I failed to list many of my fantastic teachers who inspired my thinking. The whole host of hard-working and talented people at SuperMemo World would also deserve a mention. Users of SuperMemo constantly contribute incredible suggestions that drive further progress. The reward for most impactful explanation of spaced repetition should go to Gary Wolf of Wired, but there were many more. Perhaps some other day, I will have more time to write about all those great people in detail.
1985: Birth of SuperMemo
The drive for better learning
I spent 22 long years in the education system. Old truths about schooling match my case perfectly. I never liked school, but I always liked to learn. I never let school interfere with my learning. At entry to university, after 12 years in the public school system, I still loved learning. Schooling did not destroy that love for two main reasons: (1) the system was lenient for me, and, (2) I had full freedom to learn what I like at home. In Communist Poland, I never truly experienced the toxic whip of heavy schooling. The system was negligent and I loved the ensuing freedoms.
We all know that best learning comes from passion. It is powered by the learn drive. My learn drive was strong and it was mixed with a bit of frustration. The more I learned, there more I could see the power of forgetting. I could not remedy forgetting by more learning. My memory was not bad in comparison with other students, but it was clearly a leaky vessel.
In 1982, I paid more attention to what most students discover sooner or later: testing effect. I started formulating my knowledge for active recall. I would write questions on the left side of a page and answers in a separate column to the right:

This way, I could cover the answers with a sheet of paper, and employ active recall to get a better memory effect from review. This was a slow process but the efficiency of learning increased dramatically. My notebooks from the time are described as “fast assimilation material”, which referred to the way my knowledge was written down.
In the years 1982-1983, I kept expanding my “fast assimilation” knowledge in the areas of biochemistry and English. I would review my pages of information from time to time to reduce forgetting. My retention improved but it was only a matter of time when I would hit the wall again. The more pages I had, the less frequent the review, the more obvious the problem of leaking memory. Here is an example of a repetition history from that time:
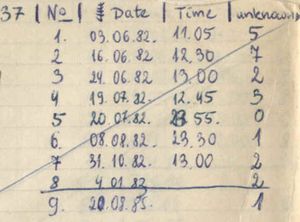
Between June 1982 and December 1984, my English-Polish word-pairs notebook included 79 pages looking like this:

Figure: A typical page from my English-Polish words notebook started in June 1982. Word pairs would be listed on the left. Review history would be recorded on the right. Recall errors would be marked as dots in the middle
Those 79 pages would encompass a mere 2794 words. This is just a fraction of what I needed, and already quite a headache to review. Interestingly, I started learning English in an active way, i.e. using Polish-English word pairs only in 1984, i.e. with two years delay. I was simply late to discover that passive knowledge of vocabulary is ok in reading, but it is not enough to speak a language. This kind of ignorance after 6 years of schooling is a norm. Schools do a lot of drilling, but shed very little light on what makes efficient learning.
In late 1984, I decided to improve the review process and carry out an experiment that has changed my life. In the end, three decades later, I am super-proud to notice that it actually affected millions. It has opened the floodgates. We have an era of faster and better learning.
This is how this initial period was described in my Master’s Thesis in 1990:
Archive warning: Why use literal archives?
This text is part of: ” Optimization of learning ” by Piotr Wozniak (1990)
It was 1982 when I made my first observations concerning the mechanism of memory that were later used in the formulation of the SuperMemo method. As a then student of molecular biology I was overwhelmed by the amount of knowledge that was required to pass exams in mathematics, physics, chemistry, biology, etc. The problem was not in being unable to master the knowledge. Usually 2-3 days of intensive studying were enough to pack the head with data necessary to pass an exam. The frustrating point was that only an infinitesimal fraction of newly acquired wisdom could remain in memory after few months following the exam.
My first observation, obvious for every attentive student, was that one of the key elements of learning was active recall. This observation implies that passive reading of books is not sufficient if it is not followed by an attempt to recall learned facts from memory. The principle of basing the process of learning on recall will be later referred to as the active recall principle. The process of recalling is much faster and not less effective if the questions asked by the student are specific rather than general. It is because answers to general questions contain redundant information necessary to describe relations between answer subcomponents.
To illustrate the problem let us imagine an extreme situation in which a student wants to master knowledge contained in a certain textbook, and who uses only one question in the process of recall: What did you learn from the textbook? Obviously, information describing the sequence of chapters of the book would be helpful in answering the question, but it is certainly redundant for what the student really wants to know. The principle of basing the process of recall on specific questions will be later referred to as the minimum information principle . This principle appears to be justified not only because of the elimination of redundancy.
Having the principles of active recall and minimum information in mind, I created my first databases (i.e. collections of questions and answers) used in an attempt to retain the acquired knowledge in memory. At that time the databases were stored in a written form on paper. My first database was started on June 6, 1982, and was composed of pages that contained about 40 pairs of words each. The first word in a pair (interpreted as a question) was an English term, the second (interpreted as an answer) was its Polish equivalent. I will refer to these pairs as items.I repeated particular pages in the database in irregular intervals (dependent mostly on the availability of time) always recording the date of the repetition, items that were not remembered and their number. This way of keeping the acquired knowledge in memory proved sufficient for a moderate-size database on condition that the repetitions were performed frequently enough.
The birthday of spaced repetition: July 31, 1985
Intuitions
In 1984, my reasoning about memory was based on two simple intuitions that probably all students have:
- if we review something twice, we remember it better. That’s pretty obvious, isn’t it? If we review it 3 times, we probably remember it even better
- if we remember a set of notes, they will gradually disappear from memory, i.e. not all at once. This is easy to observe in life. Memories have different lifetimes
These two intuitions should make everyone wonder: how fast and how many notes we lose and when we should review next?
To this day, I am amazed that very few people ever bothered to measure that ” optimum interval“. When I measured it myself, I was sure I would find more accurate results in books on psychology. I did not.
Experiment
The following simple experiment led to the birth of spaced repetition. It was conducted in 1985 and first described in my Master’s Thesis in 1990. It was used to establish optimum intervals for the first 5 repetitions of pages of knowledge. Each page contained around 40 word-pairs and the optimum interval was to approximate the moment in time when roughly 5-10% of that knowledge was forgotten. Naturally, the intervals would be highly suited for that particular type of learning material and for a specific person, in this case, me. In addition, to speed things up, the measurement samples were small. Note that this was not a research project. It was not intended for publication. The goal was to just speed up my own learning. I was convinced someone else must have measured the intervals much better, but 13 years before the birth of Google, I thought measuring the intervals would be faster than digging into libraries to find better data. The experiment ended on Aug 24, 1985, which I originally named the birthday of spaced repetition. However, while writing this text in 2018, I found the original learning materials, and it seems my eagerness to learn made me formulate an outline of an algorithm and start learning human biology on Jul 31, 1985.
For that reason, I can say that the most accurate birthday of SuperMemo and computational spaced repetition was Jul 31, 1985.
By July 31, before the end of the experiment, the results seemed predictable enough. In later years, the findings of this particular experiment appeared pretty universal and could be extended to more areas of knowledge and to the whole healthy adult population. Even in 2018, the default settings of Algorithm SM-17 do not depart far from those rudimentary findings.
Spaced repetition was born on Jul 31, 1985
Here is the original description of the experiment from my Master’s Thesis with minor corrections to grammar and style. Emphasis in the text was added in 2018 to highlight important parts. If it seems boring and unreadable, compare Ebbinghaus 1885. This is the same style of writing in the area of memory. Only goals differed. Ebbinghaus tried to understand memory. 100 years later, I just wanted to learn faster:
Archive warning: Why use literal archives?
This text is part of: ” Optimization of learning ” by Piotr Wozniak (1990)
Experiment intended to approximate the length of optimum inter-repetition intervals (Feb 25, 1985 – Aug 24, 1985):
- The experiment consisted of stages A, B, C, … etc. Each of these stages was intended to calculate the second, third, fourth and further quasi-optimal inter-repetition intervals (the first interval was set to one day as it seemed the most suitable interval judging from the data collected earlier). The criterion for establishing quasi-optimal intervals was that they should be as long as possible and allow for not more than 5% loss of remembered knowledge.
- The memorized knowledge in each of the stages A, B, C, consisted of 5 pages containing about 40 items in the following form:Question: English word,Answer: its Polish equivalent.
- Each of the pages used in a given stage was memorized in a single session and repeated next day. To avoid confusion note, that in order to simplify further considerations I use the term first repetition to refer to memorization of an item or a group of items. After all, both processes, memorization and relearning, have the same form – answering questions as long as it takes for the number of errors to reach zero.
- In the stage A (Feb 25 – Mar 16), the third repetition was made in intervals 2, 4, 6, 8 and 10 days for each of the five pages respectively. The observed loss of knowledge after these repetitions was 0, 0, 0, 1, 17 percent respectively. The seven-day interval was chosen to approximate the second quasi-optimal inter-repetition interval separating the second and third repetitions.
- In the stage B (Mar 20 – Apr 13), the third repetition was made after seven-day intervals whereas the fourth repetitions followed in 6, 8, 11, 13, 16 days for each of the five pages respectively. The observed loss of knowledge amounted to 3, 0, 0, 0, 1 percent. The 16-day interval was chosen to approximate the third quasi-optimal interval. NB: it would be scientifically more valid to repeat the stage B with longer variants of the third interval because the loss of knowledge was little even after the longest of the intervals chosen; however, I was then too eager to see the results of further steps to spend time on repeating the stage B that appeared sufficiently successful (i.e. resulted in good retention)
- In the stage C (Apr 20 – Jun 21), the third repetitions were made after seven-day intervals, the fourth repetitions after 16-day intervals and the fifth repetitions after intervals of 20, 24, 28, 33 and 38 days. The observed loss of knowledge was 0, 3, 5, 3, 0 percent. The stage C was repeated for longer intervals preceding the fifth repetition (May 31 – Aug 24). The intervals and memory losses were as follows: 32-8%, 35-8%, 39-17%, 44-20%, 51-5% and 60-20%. The 35-day interval was chosen to approximate the fourth quasi-optimal interval.
It is not difficult to notice, that each of the stages of the described experiment took about twice as much time as the previous one. It could take several years to establish first ten quasi-optimal inter-repetition intervals. Indeed, I continued experiments of this sort in following years in order to gain deeper understanding of the process of optimally spaced repetitions of memorized knowledge. However, at that time, I decided to employ the findings in my day-to-day process of routine learning.
On July 31, 1985, I could already sense the outcome of the experiment. I started using SuperMemo on paper to learn human biology. That would be the best date to call for the birthday of SuperMemo.
The events of July 31, 1985
On July 31, 1985, SuperMemo was born. I had most of my data from my spaced repetition experiment available. As an eager practitioner, I did not wait for the experiment to end. I wanted to start learning as soon as possible. Having built a great deal of notes in human biology, I started converting those notes into Special Memorization Test format (SMT was the original name for SuperMemo, and spaced repetition).

Figure: Human biology in the Special Memorization Test format started on Jul 31, 1985 (i.e. the birth of SuperMemo)
My calculations told me that, at 20 min/day, I would need 537 days to process my notes and finish the job by January 1987. I also computed that each page of the test would likely cost me 2 hours of life. Despite all the promise and speed of SuperMemo, this realization was pretty painful. The speed of learning in college is way too fast for the capacity of human memory. Now that I could learn much faster and better, I also realized I wouldn’t cover even a fraction of what I thought was possible. Schools make no sense with their volume and speed. On the same day, I found out that the Polish communist government lifted import tariffs on microcomputers. This should make it possible, at some point, to buy a computer in Poland. This opened a way to SuperMemo for DOS 2.5 years later.
Also on July 31, I noted that if vacation could last forever, I would achieve far more in learning and even more in life. School is such a waste of time. However, the threat of conscription kept me in line. I would enter a path that would make me enroll in university for another 5 years. However, most of that time was devoted to SuperMemo and I have few regrets.
My spaced repetition experiment ended on Aug 24, 1985. I also started learning English vocabulary. By that day, I managed to have most of my biochemistry material written down in pages for SuperMemo review.
Note: My Master’s Thesis mistakenly refers to Oct 1, 1985 as the day when I started learning human biology (not July 31 as seen in the picture above). Oct 1, 1985 was actually the first day of my computer science university and was otherwise unremarkable. With the start of the university, my time for learning and energy for learning were cut dramatically. Paradoxically, the start of school always seems to augur the end of good learning.
First spaced repetition algorithm: Algorithm SM-0, Aug 25, 1985
As a result of my spaced repetition experiment, I was able to formulate the first spaced repetition algorithm that required no computer. All learning had to be done on paper. I did not have a computer back in 1985. I was to get my first microcomputer, ZX Spectrum, only in 1986. SuperMemo had to wait for the first computer with a floppy disk drive (Amstrad PC 1512 in the year 1987).
I often get asked this simple question: “How can you formulate SuperMemo after an experiment that lasted 6 months? How can you predict what would happen in 20 years?”
The first experiments in reference to the length of optimum interval resulted in conclusions that made it possible to predict the most likely length of successive inter-repetition intervals without actually measuring retention beyond weeks! In short, it could be illustrated with the following reasoning. If the first months of research yielded the following optimum intervals: 1, 2, 4, 8, 16 and 32 days, you could hope with confidence that the successive intervals would increase by a factor of two.
Archive warning: Why use literal archives?
This text is part of: ” Optimization of learning ” by Piotr Wozniak (1990)
Algorithm SM-0 used in spaced repetition without a computer (Aug 25, 1985)
- Split the knowledge into smallest possible question-answer items
- Associate items into groups containing 20-40 elements. These groups are later called pages
- Repeat whole pages using the following intervals (in days):I(1)=1 dayI(2)=7 daysI(3)=16 daysI(4)=35 daysfor i>4: I(i):=I(i-1)*2where:
- I(i) is the interval used after the i-th repetition
- Copy all items forgotten after the 35th day interval into newly created pages (without removing them from previously used pages). Those new pages will be repeated in the same way as pages with items learned for the first time
Note, that inter-repetition intervals after the fifth repetition were assumed to increase twice in subsequent repetitions. This fact was based on an intuition rather than on experiment. In two years of using the Algorithm SM-0 sufficient data were collected to confirm a reasonable accuracy of this assumption.
To this day I hear some people use or even prefer the paper version of SuperMemo. Here is a description from 1992.
Note that the intuition that intervals should increase twice is as old as the theory of learning. In 1932, C. A. Mace hinted on the efficient learning methods in his book ” The psychology of study“. He mentioned ” active rehearsal” and ” repetitive revisions” that should be spaced in gradually increasing intervals, roughly ” intervals of one day, two days, four days, eight days, and so on“. This proposition was later taken on by other authors. Those included Paul Pimsleur and Tony Buzan who both proposed their own intuitions that involved very short intervals (in minutes) or “final repetition” (after a few months). All those ideas did not permeate well into the practice of study beyond the learning elites. Only a computer application made it possible to start learning effectively without studying the methodology.
That intuitive interval multiplication factor of 2 has also shown up in the context of studying the possibility of evolutionary optimization of memory in response to statistic properties of the environment: ” Memory is optimized to meet probabilistic properties of the environment “
Despite all its simplicity, in my Master’s Thesis, I did not hesitate to call my new method “revolutionary”:
Archive warning: Why use literal archives?
This text is part of: ” Optimization of learning ” by Piotr Wozniak (1990)
Although the acquisition rate may not have seemed staggering, the Algorithm SM-0 was revolutionary in comparison to my previous methods because of two reasons:
- with the lapse of time, knowledge retention increased instead of decreasing (as it was the case with intermittent learning)
- in a long term perspective, the acquisition rate remained almost unchanged (with intermittent learning, the acquisition rate would decline substantially over time)
[…]
For the first time, I was able to reconcile high knowledge retention with infrequent repetitions that in consequence led to steadily increasing volume of knowledge remembered without the necessity to increase the timeload!
Retention of 80% was easily achieved, and could even be increased by shortening the inter-repetition intervals. This, however, would involve more frequent repetitions and, consequently, increase the timeload. The assumed repetition spacing provided a satisfactory compromise between retention and workload.
[…]The next significant improvement of the Algorithm SM-0 was to come only in 1987 after the application of a computer to supervise the learning process. In the meantime, I accumulated about 7190 and 2817 items in my new English and biological databases respectively. With the estimated working time of 12 minutes a day for each database, the average knowledge acquisition rate amounted to 260 and 110 items/year/minute respectively, while knowledge retention amounted to 80% at worst.
Birth of SuperMemo from a decade’s perspective
A decade after the birth of SuperMemo, it became pretty well-known in Poland. Here is the same story as retold by J. Kowalski, Enter in 1994:
It was 1982, when a 20-year-old student of molecular biology at Adam Mickiewicz University of Poznan, Piotr Wozniak, became quite frustrated with his inability to retain newly learned knowledge in his brain. This referred to the vast material of biochemistry, physiology, chemistry, and English, which one should master wishing to embark on a successful career in molecular biology. One of the major incentives to tackle the problem of forgetting in a more systematic way was a simple calculation made by Wozniak which showed him that by continuing his work on mastering English using his standard methods, he would need 120 years to acquire all the important vocabulary. This not only prompted Wozniak to work on methods of learning, but also, turned him into a determined advocate of the idea of one language for all people (bearing in mind the time and money spent by the mankind on translation and learning languages). Initially, Wozniak kept increasing piles of notes with facts and figures he would like to remember. It did not take long to discover that forgetting requires frequent repetitions and a systematic approach is needed to manage all the newly collected and memorized knowledge. Using an obvious intuition, Wozniak attempted to measure the retention of knowledge after different inter-repetition intervals, and in 1985 formulated the first outline of SuperMemo, which did not yet require a computer. By 1987, Wozniak, then a sophomore of computer science, was quite amazed with the effectiveness of his method and decided to implement it as a simple computer program. The effectiveness of the program appeared to go far beyond what he had expected. This triggered an exciting scientific exchange between Wozniak and his colleagues at Poznan University of Technology and Adam Mickiewicz University. A dozen of students at his department took on the role of guinea pigs and memorized thousands of items providing a constant flow of data and critical feedback. Dr Gorzelańczyk from Medical Academy was helpful in formulating the molecular model of memory formation and modeling the phenomena occurring in the synapse. Dr Makałowski from the Department of Biopolymer Biochemistry contributed to the analysis of evolutionary aspects of optimization of memory (NB: he was also the one who suggested registering SuperMemo for Software for Europe). Janusz Murakowski, MSc in physics, currently enrolled in a doctoral program at the University of Delaware, helped Wozniak solve mathematical problems related to the model of intermittent learning and simulation of ionic currents during the transmission of action potential in nerve cells. A dozen of forthcoming academic teachers, with Prof. Zbigniew Kierzkowski in forefront, helped Wozniak tailor his program of study to one goal: combining all aspects of SuperMemo in one cohesive theory that would encompass molecular, evolutionary, behavioral, psychological, and even societal aspects of SuperMemo. Wozniak who claims to have discovered at least several important and never-published properties of memory, intended to solidify his theories by getting a PhD in neuroscience in the US. Many hours of discussions with Krzysztof Biedalak, MSc in computer science, made them both choose another way: try to fulfill the vision of getting with SuperMemo to students around the world.
1986: First steps of SuperMemo
SuperMemo on paper
On Feb 22, 1984, I computed that at my learning rate and my investment in learning, it would take me 26 years to master English (in SuperMemo, Advanced English standard is 4 years at 40 min/day). With the arrival of SuperMemo on paper that statistic improved dramatically.
In summer 1985, using SuperMemo on paper, I started learning with great enthusiasm. For the first time ever, I knew that all investment in learning would pay. Nothing could slip through the cracks. This early enthusiasm makes me wonder why I did not share my good news with others.
SuperMemo wasn’t a “secret weapon” that many users employ to impress others. I just thought that science must have answered all questions related to efficient learning. My impression was that I only patched my own poor access to western literature with a bit of own investigation. My naivete of the time was astronomical. My English wasn’t good enough to understand news from the west. America was for me a land of super-humans who do super-science, land on the moon, do all major discoveries and will soon cure cancer and become immortal. At the same time, it was a land of Reagan who could blast Poland off the surface of the Earth with Pershing or cruise missiles. That gave me a couple of nightmares. Perhaps the only major source of stress in the early 1980s. I often ponder amazing inconsistencies in the brains of toddlers or kids. To me, the naivete of my early twenties tells me I must have been a late bloomer with very uneven development. Ignorance of English translated to the ignorance of the world. I was a young adult with areas of strength and areas of incredible ignorance. In that context, spaced repetition looks like a child of a need combined with ignorance, self-confidence, and passion.
University
In October 1985, I started my years at a computer science university. I lost my passion for the university in the first week of learning. Instead of programming, we were subject to excruciatingly boring lectures of introductory topics in math, physics, electronics, etc. With a busy schedule, I might have easily become a SuperMemo dropout. Luckily, my love for biochemistry and my need for English would not let me slow down. I continued my repetitions, adding new pages from time to time. Most of all, I had a new dream: to have my own computer and do some programming on my own. One of the first things I wanted to implement was SuperMemo. I would keep my pages on the computer and have them scheduled automatically.
I casually mentioned my super-learning method to my high school friend Andrzej “Mike” Kubiak only in summer 1987 (Aug 29). We played football and music together. I finally showed him how to use SuperMemo on Nov 14, 1987. It took 836 days (2 years 3 months and 2 weeks) for me to recruit the first user of SuperMemo. Mike was later my guinea pig in trying out SuperMemo in procedural learning. He kept practicing computer-generated rhythms using a SuperMemo-like schedule. For Mike, SuperMemo was a love at first sight. His vocabulary rocketed. He remained faithful for many years up to a point when the quality of his English outstripped the need for further learning. He is a yogi and his trip to India and regular use of English have consolidated the necessary knowledge for life.
ZX Spectrum
In 1986 and 1987, I kept thinking about SuperMemo on a computer more and more often. Strangely, initially, I did not think much about the problem of separating pages into individual flashcards. This illustrates how close-minded we can be when falling into a routine of doing the same things daily. To get to the status of 2018, SuperMemo had to undergo dozens of breakthroughs and similarly obvious microsteps. It is all so simple and obvious in hindsight. However, there are hidden limits of human thinking that prevented incremental reading from emerging a decade earlier. Only a fraction of those limits is in technology.
In my first year of university I had very little time and energy to spare, and most of that time I invested in getting my first computer: ZX Spectrum (Jan 1986). I borrowed one from a friend for a day in Fall 1985 and was totally floored. I started programming “on paper” long before I got the toy. My first program was “planning the day” precursor of Plan. The program was ready to type in into the computer when I turned on my ZX Spectrum for the first time on Jan 4, 1986. As of that day, I spent most of my days on programming, ignoring school and writing my programs on paper even during classes.

Figure: ZX Spectrum 8-bit personal home computer.
The Army
Early 1986 was marred by the threat of conscription. I thought 5 more years of university meant 5 more years of freedom. However, The Army had different ideas. For them, second major did not count, and I had to bend over backwards to avoid the service. My anger was tripled by the fact that I would never ever contemplate 12 months of separation from my best new friend: ZX Spectrum. I told the man in uniform that they really do not want to have an angry man with a gun in their ranks. Luckily, in the mess of the communist bureaucracy, I managed to slip the net and continue my education. To this day, I am particularly sensitive to issues of freedom. Conscription isn’t much different from slavery. It was not a conscription in the name of combating fascism. It was a conscription for mindless drilling, goosestep, early alarms, hot meals in a hurry and stress. If this was to serve the readiness of Communist Bloc, this would be a readiness of Good Soldier Švejk Army. Today, millions of kids are sent to school in a similar conscription-like effort verging on slavery. Please read my ” I would never send my kids to school“ for my take on the coercive trample of the human rights of children. I am sure that some of my sentiments have been shaped by the sense of enslavement from 1986.
On the day when the radioactive cloud from Chernobyl passed over Poznan, Poland, I was busy walking point to point across the vast city visiting military and civilian offices in my effort to avoid the army. I succeeded and summer 1986 was one of the sunniest ever. I spent my days on programming, jogging, learning with SuperMemo (on paper), swimming, football and more programming.
Summer 1986
My appetite for new software was insatiable. I wrote a program for musical composition, for predicting the outcomes of the World Cup, for tic-tac-toe in 3D, for writing school tests, and many more. I got a few jobs from the Department of Biochemistry (Adam Mickiewicz University). My hero, Prof. Augustyniak, needed software for simulating the melting of DNA, and for fast search of tRNA genes (years later that led to a publication). He also commissioned a program for regression analysis that later inspired progress in SuperMemo (esp. Algorithms SM-6 and SM-8).
While programming, I had SuperMemo at the back of my mind all the time, however, all my software was characterized by the absence of any database. The programs had to be read from a cassette tape which was a major drag (it did not bother me back in 1986). It was simpler to keep my SuperMemo knowledge on paper. I started dreaming of a bigger computer. However, in Communist Poland, the cost was out of reach. Once I computed that an IBM PC would cost as much as my mom’s lifetime wages in the communist system. As late as in 1989, I could not afford a visit in a toilet in Holland because it was so astronomically expensive when compared with wages in Poland.
PC 1512
My whole family pulled in resources. My cousin, Dr Garbatowski, arranged a special foreign currency account for Deutsch Mark transfers. By a miracle, I was able to afford DM 1000 Amstrad PC 1512 from Germany. The computer was not smuggled as it was once reported in the press. My failed smuggling effort came two years earlier in reference to ZX Spectrum. My friends from Zaire were to buy it for me in West Berlin. In the end, I bought second-hand ZX Spectrum in Poland, at a good price, from someone who thought he was selling “just a keyboard”.

Figure: Amstrad PC-1512 DD. My version had only one diskette drive. Operating system MS-DOS had to be loaded from one diskette, Turbo Pascal 3.0 from another diskette, SuperMemo from yet another. By the time I had my first hard drive in 1991, my English collection was split into 3000-item pieces over 13 diskettes. I had many more for other areas of knowledge. On Jan 21, 1997, SuperMemo World has tracked down that original PC and bought it back from its owner: Jarek Kantecki. The PC was fully functional for the whole decade. It is now buried somewhere in dusty archives of the company. Perhaps we will publish its picture at some point. The presented picture comes from Wikipedia
My German Amstrad-Schneider PC 1512 was ordered from a Polish company Olech. Olech was to deliver it in June 1987. They did it in September. This cost me the whole summer of stress. Some time later, Krzysztof Biedalak ordered a PC from a Dutch company Colgar and never got a PC or money back. If this happened to me, I would have lost my trust in humanity. This would have killed SuperMemo. This might have killed my passion for computers. Biedalak, on the other hand, stoically got back to hard work and earned his money back and more. That would be one of the key personality differences between me and Biedalak. Stress resilience should be one of the components of development. I developed my stress resilience late with self-discipline training (e.g. winter swimming or marathons). Having lost his money, Biedalak did not complain. He got it back in no time. Soon I was envious of his new shiny PC. His hard work and determination in achieving goals was always a key to the company’s survival. It was his own privately earned money that helped SuperMemo World survive the first months. He did not get a gift from his parents. He could always do things on his own.
Simulating the learning process
On Feb 22, 1986, using my ZX Spectrum, I wrote a program to simulate long-term learning process with SuperMemo. I was worried that with the build-up of material, the learning process would slow down significantly. However, my preliminary results were pretty counterintuitive: the progress is almost linear. There isn’t much slow down in learning beyond the very initial period.
On Feb 25, 1986, I extended the simulation program by new functions that would answer ” burning questions about memory“. The program would run on Spectrum over 5 days until I could get full results for 80 years of learning. It confirmed my original findings.
On Mar 23, 1986, I managed to write the same simulation program in Pascal which was a compiled language. This time, I could run 80 years simulation in just 70 minutes. I got the same results. Today, SuperMemo still makes it possible to run similar simulations. The same procedure takes just a second or two.
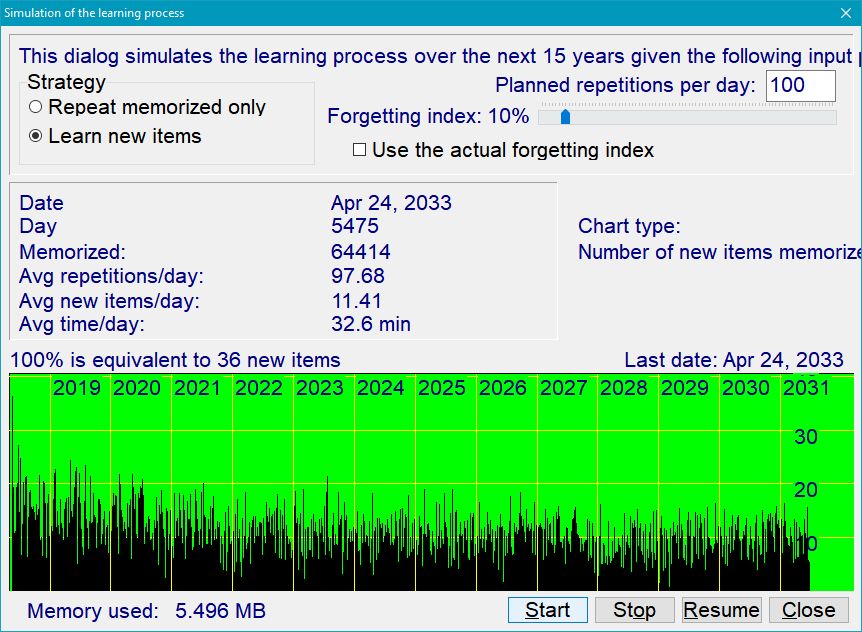
Figure: SuperMemo makes it possible to simulate the course of learning over 15 years using real data collected during repetitions.
Some of the results of that simulation are valid today. Below I present some of the original findings. Some might have been amended in 1990 or 1994.
Learning curve is almost linear
The learning curve obtained by using the model, except for the very initial period, is almost linear.
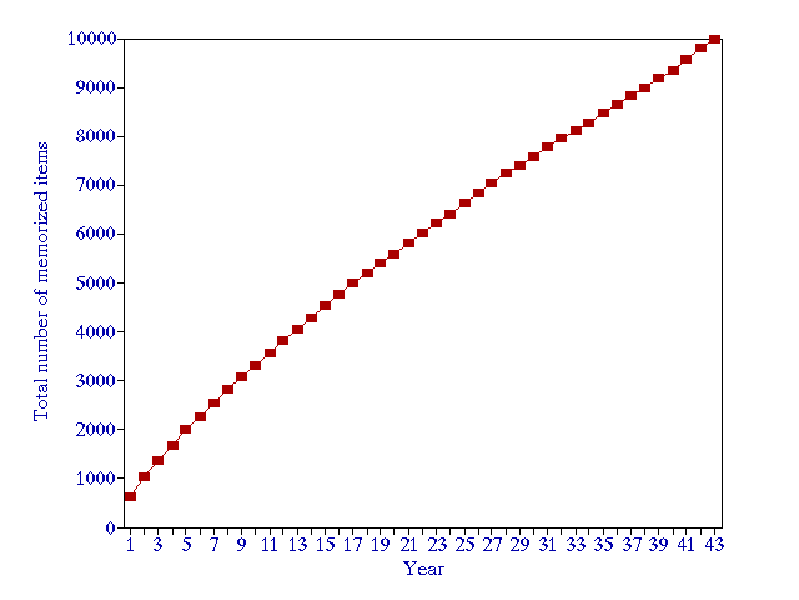
Figure: Learning curve for a generic material, forgetting index equal to 10%, and daily working time of 1 minute.
New items take 5% of the time
In a long-term process, for the forgetting index equal to 10%, and for a fixed daily working time, the average time spent on memorizing new items is only 5% of the total time spent on repetitions. This value is almost independent of the size of the learning material.
Speed of learning
According to the simulation, the number of items memorized in consecutive years when working one minute per day can be approximated with the following equation:
NewItems=aar*(3*e -0.3*year+1)
where:
- NewItems – items memorized in consecutive years when working one minute per day,
- year – ordinal number of the year,
- aar – asymptotic acquisition rate, i.e. the minimum learning rate reached after many years of repetitions (usually about 200 items/year/min)
In a long-term process, for the forgetting index equal to 10%, the average rate of learning for generic material can be approximated to 200-300 items/year/min, i.e. one minute of learning per day results in the acquisition of 200-300 items per year. Users of SuperMemo usually report the average rate of learning from 50-2000 items/year/min.
Workload
For a generic material and the forgetting index of about 10%, the function of time required daily for repetitions per item can roughly be approximated using the formula:
time=1/500*year -1.5+1/30000
where:
- time – average daily time spent for repetitions per item in a given year (in minutes),
- year – year of the process.
As the time necessary for repetitions of a single item is almost independent of the total size of the learned material, the above formula may be used to approximate the workload for learning material of any size. For example, the total workload for a 3000-element collection in the first year will be 3000/500*1+3000/30000=6.1 (min/day).
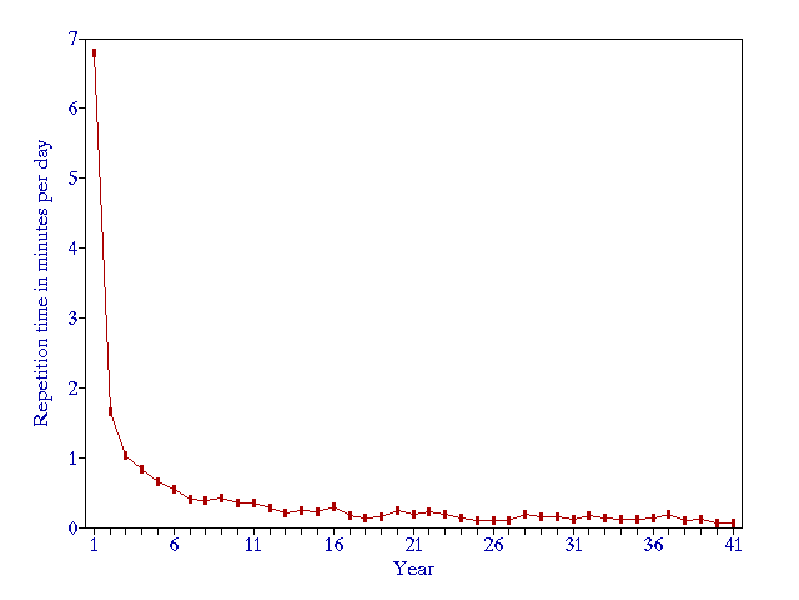
Optimum forgetting index
Figure: Workload, in minutes per day, in a generic 3000-item learning material, for the forgetting index equal to 10%.
The greatest overall knowledge acquisition rate is obtained for the forgetting index of about 20-30%. This results from the trade-off between reducing the repetition workload and increasing the relearning workload as the forgetting index progresses upward. In other words, high values of the forgetting index result in longer intervals, but the gain is offset by an additional workload coming from a greater number of forgotten items that have to be relearned.
For the forgetting index greater than 20%, the positive effect of long intervals on memory resulting from the spacing effect is offset by the increasing number of forgotten items.
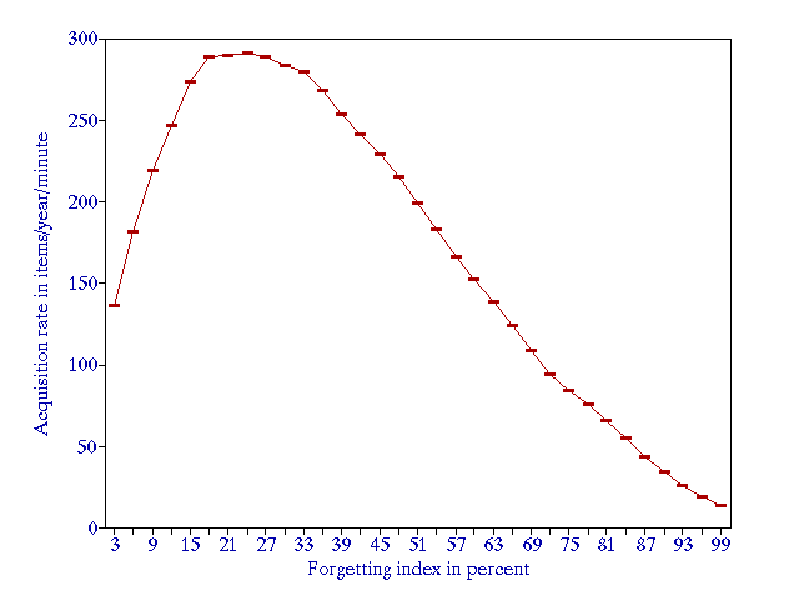
Figure: Dependence of the knowledge acquisition rate on the forgetting index.
When the forgetting index drops below 5%, the repetition workload increases rapidly (see the figure above). The recommended value of the forgetting index used in the practice of learning is 6-14%.
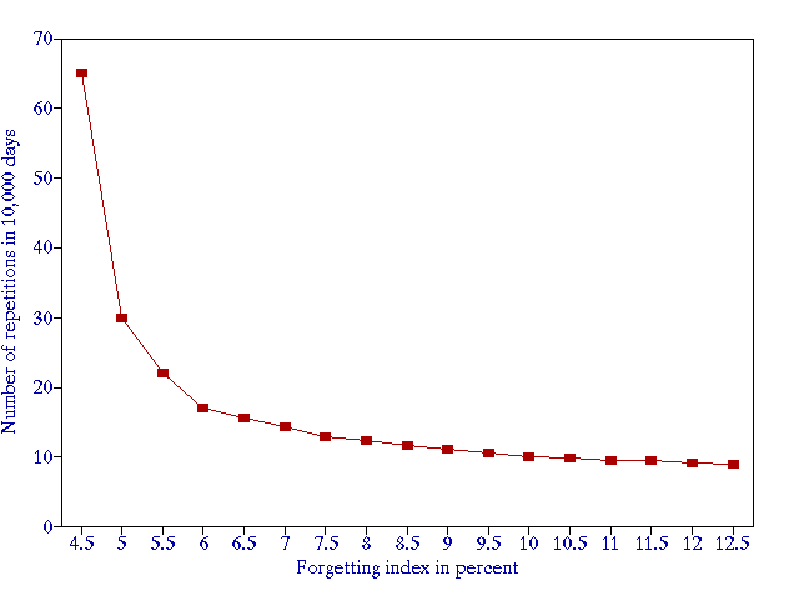
Figure: Trade-off between the knowledge retention ( forgetting index) and the workload (number of repetitions of an average item in 10,000 days).
In later years, the value of the optimum forgetting index was found to differ depending on the tools used (e.g. Algorithm SM-17).
Memory capacity
The maximum lifetime capacity of the human brain to acquire new knowledge by means of learning procedures based on the discussed model can be estimated as no more than several million items. As nobody is likely to spend all his life on learning, I doubt I will ever see anyone with a million items in his memory.
1987: SuperMemo 1.0 for DOS
SuperMemo 1.0 for DOS: day by day (1987)
SuperMemo history file says ” Wozniak wrote his first SuperMemo in 16 evenings“. The reality was slightly more complex and I thought I would describe it in more details using the notes of the day.
I cannot figure out what I meant writing on Jul 3, 1987 that ” I have an idea of a revolutionary program arranging my work and scientific experiments SMTests” (SMTests stands for SuperMemo on paper). A transition from paper to a computer seems like an obvious step. There must have been some mental obstacle on the way that required “thinking out of the box”. Unfortunately, I did not write down details. Today it only matters in that it illustrates how excruciatingly slow a seemingly obvious idea may creep into the mind.
On Sep 8, 1987, my first PC arrived from Germany (Amstrad PC 1512). My enthusiasm was unmatched! I could not sleep. I worked all night. The first program I planned to write was to be used for mathematical approximations. SuperMemo was second in the pipeline.

Figure: Amstrad PC-1512 DD. My version had only one diskette drive. Operating system MS-DOS had to be loaded from one diskette, Turbo Pascal 3.0 from another diskette, SuperMemo from yet another. By the time I had my first hard drive in 1991, my English collection was split into 3000-item pieces over 13 diskettes. I had many more for other areas of knowledge. On Jan 21, 1997, SuperMemo World has tracked down that original PC and bought it back from its owner: Jarek Kantecki. The PC was fully functional for the whole decade. It is now buried somewhere in dusty archives of the company. Perhaps we will publish its picture at some point. The presented picture comes from Wikipedia
Oct 16, 1987, Fri, in 12 hours I wrote my first SuperMemo in GW-Basic (719 minutes of non-stop programming). It was slow like a snail and buggy. I did not like it much. I did not start learning. Could this be the end of SuperMemo? Wrong choice of a programming language? Busy days at school kept me occupied with a million unimportant things. Typical school effect: learn nothing about everything. No time for creativity and your own learning. Luckily, all the time I used SuperMemo on paper. The idea of SuperMemo could not have died. It had to be automated sooner or later.
On Nov 14, 1987, Sat, SuperMemo on paper got its first user: Mike Kubiak. He was very enthusiastic. The fire kept burning. On Nov 18, I learned about Turbo Pascal. It did not work on my computer. In those days, if you had a wrong graphics card, you might struggle. Instead of Hercules, I had a text-mode monochrome (black-and-white) CGA. I managed to solve the problem by editing programs in the RPED text editor rather than in the Turbo Pascal environment. Later I got the right version for my display card. Incidentally, old SuperMemos show in colors. I was programming it in shades of gray and never knew how it really looked in the color mode.
Nov 21, 1987 was an important day. It was a Saturday. Days free from school are days of creativity. I hoped to get up at 9 am but I overslept by 72 minutes. This is bad for the plan, but this is usually good for the brain and performance. I started the day from SuperMemo on paper (reviewing English, human biology, computer science, etc.). Later in the day, I read my Amstrad PC manual, learned about Pascal and Prolog, spent some time thinking how human cortex might work, did some exercise, and in the late evening, in a slightly tired state of mind, in afterthought, decided to write SuperMemo for DOS. This would be my second attempt. However, this time I chose Turbo Pascal 3.0 and never regretted. To this day, as a direct consequence, SuperMemo 17 code is written in Pascal (Delphi).
For the record, the name SuperMemo was proposed much later. In those days, I called my program: SMTOP for Super-Memorization Test Optimization Program. In 1988, Tomasz Kuehn insisted we call it CALOM for Computer-Aided Learning Optimization Method.
Nov 22, 1987 was a mirror copy of Nov 21. I concluded that I know how cortex works and that one day it would be nice to build a computer using similar principles (check Jeff Hawkins‘s work). The fact that I returned to programming SuperMemo in the late evening, i.e. very bad time for creative work, seems to indicate that the passion has not kicked in yet.
Nov 23, 1987 looked identical. I am not sure why I did not have any school obligations on Monday, but this might have saved SuperMemo. On Nov 24, 1987, the excitement kicked in and I worked for 8 hours straight (in the evening again). The program had a simple menu and could add new items to the database.
Nov 25, 1987 was wasted: I had to go to school, I was tired and sleepy. We had excruciatingly boring classes in computer architecture, probably a decade behind the status quo in the west.
Nov 26 was free again and again I was able to catch up with SuperMemo work. The program grew to be 15,400 bytes huge. I concluded the program might be ” very usefull” (sic!).
On Nov 27, I added 3 more hours of work after school.
Nov 28 was Saturday and I could add 12 enthusiastic hours of non-stop programming. SuperMemo now looked like almost ready for use.
On Nov 29, Sunday, I voted for economic reforms and democratization in Poland. In the evening, I did not make much progress. I had to prepare an essay for my English class. The essay described the day when I experimented with alcohol one day in 1982. I was a teetotaller, but as a biologist, I concluded I need to know how alcohol affects the mind.
Nov 30 was wasted at school, but we had a nice walk home with Biedalak. We had a long conversation in English about our future. That future was mostly to be about science, probably in the US.
Dec 1-4 were wasted at school again. No time for programming. In a conversation with some Russian professor, I realized that I completely forgot Russian in short 6 years. I used to be proudly fluent! I had to channel my programming time into some boring software for designing electronic circuits. I had to do it to credit a class in electronics. I had a deal with the teacher that I would not attend, just write this piece of software. I did not learn anything and to this day I mourn the waste of time. If I was free, I could have invested this energy in SuperMemo.
Dec 5 was a Saturday. Free from school. Hurray! However, I had to start from wasting 4 hours on some “keycode procedure”. In those days, even decoding the key pressed might become a challenge. And then another hour wasted on changing some screen attributes. In addition, I added 6 hours for writing “item editor”. This way, I could conveniently edit items in SuperMemo. The effortless things you take for granted today: cursor left, cursor right, delete, up, new line, etc. needed a day of programming back then.
Dec 6 was a lovely Sunday. I spent 7 hours debugging SuperMemo, adding “final drill”, etc. The excitement kept growing. In a week, I might start using my new breakthrough speed-learning software.
On Monday, Dec 7, after school, I added a procedure for deleting items.
On Dec 8, while Reagan and Gorbachev signed their nuclear deal, I added a procedure for searching items and displaying some item statistics. SuperMemo “bloated” to 43,800 bytes.
Dec 9 was marred by school and programming for the electronics class.
On Dec 10, I celebrated power cuts at school. Instead of boring classes, I could do some extra programming.
On Dec 11, we had a lovely lecture with one of the biggest brains at school: Prof. Jan Węglarz. He insisted that he could do more in Poland than abroad. This was a powerful message. However, in 2018, his Wikipedia entry says that his two-phase method discovery was ignored, and later duplicated in the west because he opted for publishing in Polish. Węglarz created a formidable team of best operations research brains in Poznan indeed. If I did not sway in the direction of SuperMemo, I would sure come with a begging hat to look for an employment opportunity. In the evening, I added a procedure for inspecting the number of items to review each day (today’s Workload).
Dec 12 was a Saturday. I expanded SuperMemo by a pending queue editor, and seemed ready to start learning, however, …
… on Dec 13, I was hit by a bombshell: ” Out of memory“. I somehow managed to fix the problem by optimizing the code. The last option I needed to add was for the program to read the date. Yes. That was a big deal hack. Without it, I would need to type in the current date at the start of the work with the program. Finally, at long last, in the afternoon, on Dec 13, 1987, I was able to add my first items to my human biology collection: questions about the autonomic nervous system. By Dec 23, 1987, my combined paper and computer databases included 3795 questions on human biology (of which almost 10% already in SuperMemo). Sadly, I had to remove full repetition histories from SuperMemo on that day. There wasn’t enough space on 360K diskettes. Spaced repetition research would need to wait a few more years.
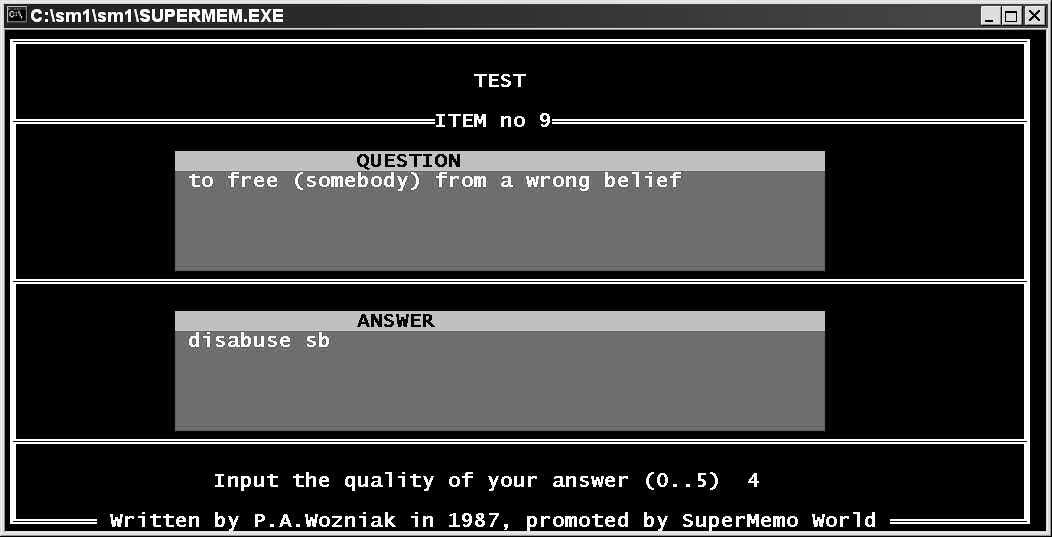
Figure: SuperMemo 1.0 for DOS (1987).
Algorithm SM-2
Here is the description of the algorithm used in SuperMemo 1.0. The description was taken from my Master’s Thesis written 2.5 years later (1990). SuperMemo 1.0 was soon replaced by a nicer SuperMemo 2.0 that I could give away to friends at university. There were insignificant updates to the algorithm that was named Algorithm SM-2 after the version of SuperMemo. This means there has never been Algorithm SM-1.
I mastered 1000 questions in biology in the first 8 months. Even better, I memorized exactly 10,000 items of English word pairs in the first 365 days working 40 min/day. This number was used as a benchmark in advertising SuperMemo in its first commercial days. Even today, 40 min is the daily investment recommended to master Advanced English in 4 years (40,000+ items).
To this day, Algorithm SM-2 remains popular and is still used by applications such as Anki, Mnemosyne and more.
Archive warning: Why use literal archives?
3.2. Application of a computer to improve the results obtained in working with the SuperMemo method
I wrote the first SuperMemo program in December 1987 (Turbo Pascal 3.0, IBM PC). It was intended to enhance the SuperMemo method in two basic ways:
- apply the optimization procedures to smallest possible items (in the paper-based SuperMemo items were grouped in pages),
- differentiate between the items on the base of their different difficulty.
Having observed that subsequent inter-repetition intervals are increasing by an approximately constant factor (e.g. two in the case of the SM-0 algorithm for English vocabulary), I decided to apply the following formula to calculate inter-repetition intervals:
I(1):=1
I(2):=6
for n>2 I(n):=I(n-1)*EF
where:
- I(n) – inter-repetition interval after the n-th repetition (in days)
- EF – easiness factor reflecting the easiness of memorizing and retaining a given item in memory (later called the E-Factor).
E-Factors were allowed to vary between 1.1 for the most difficult items and 2.5 for the easiest ones. At the moment of introducing an item into a SuperMemo database, its E-Factor was assumed to equal 2.5. In the course of repetitions, this value was gradually decreased in case of recall problems. Thus the greater problems an item caused in recall the more significant was the decrease of its E-Factor.
Shortly after the first SuperMemo program had been implemented, I noticed that E-Factors should not fall below the value of 1.3. Items having E-Factors lower than 1.3 were repeated annoyingly often and always seemed to have inherent flaws in their formulation (usually they did not conform to the minimum information principle). Thus not letting E-Factors fall below 1.3 substantially improved the throughput of the process and provided an indicator of items that should be reformulated. The formula used in calculating new E-Factors for items was constructed heuristically and did not change much in the following 3.5 years of using the computer-based SuperMemo method.
In order to calculate the new value of an E-Factor, the student has to assess the quality of his response to the question asked during the repetition of an item (my SuperMemo programs use the 0-5 grade scale – the range determined by the ergonomics of using the numeric key-pad). The general form of the formula used was:
EF’:=f(EF,q)
where:
- EF’ – new value of the E-Factor
- EF – old value of the E-Factor
- q – quality of the response
- f – function used in calculating EF’.
The function f had initially multiplicative character and was in later versions of SuperMemo program, when the interpretation of E-Factors changed substantially, converted into an additive one without significant alteration of dependencies between EF’, EF and q. To simplify further considerations only the function f in its latest shape is taken into account:
EF’:=EF-0.8+0.28*q-0.02*q*q
which is a reduced form of:
EF’:=EF+(0.1-(5-q)*(0.08+(5-q)*0.02))
Note, that for q=4 the E-Factor does not change.
Let us now consider the final form of the SM-2 algorithm that with minor changes was used in the SuperMemo programs, versions 1.0-3.0 between December 13, 1987 and March 9, 1989 (the name SM-2 was chosen because of the fact that SuperMemo 2.0 was by far the most popular version implementing this algorithm).
Algorithm SM-2 used in the computer-based variant of the SuperMemo method and involving the calculation of easiness factors for particular items:
- Split the knowledge into smallest possible items.
- With all items associate an E-Factor equal to 2.5.
- Repeat items using the following intervals:I(1):=1I(2):=6for n>2: I(n):=I(n-1)*EFwhere:
- I(n) – inter-repetition interval after the n-th repetition (in days),
- EF – E-Factor of a given item
- After each repetition assess the quality of repetition response in 0-5 grade scale:5 – perfect response4 – correct response after a hesitation3 – correct response recalled with serious difficulty2 – incorrect response; where the correct one seemed easy to recall1 – incorrect response; the correct one remembered0 – complete blackout.
- After each repetition modify the E-Factor of the recently repeated item according to the formula:EF’:=EF+(0.1-(5-q)*(0.08+(5-q)*0.02))where:
- EF’ – new value of the E-Factor,
- EF – old value of the E-Factor,
- q – quality of the response in the 0-5 grade scale.
- If the quality response was lower than 3 then start repetitions for the item from the beginning without changing the E-Factor (i.e. use intervals I(1), I(2) etc. as if the item was memorized anew).
- After each repetition session of a given day repeat again all items that scored below four in the quality assessment. Continue the repetitions until all of these items score at least four.
The optimization procedure used in finding E-Factors proved to be very effective. In SuperMemo programs you will always find an option for displaying the distribution of E-Factors (later called the E-Distribution). The shape of the E-Distribution in a given database was roughly established within few months since the outset of repetitions. This means that E-Factors did not change significantly after that period and it is safe to presume that E-Factors correspond roughly to the real factor by which the inter-repetition intervals should increase in successive repetitions.
During the first year of using the SM-2 algorithm (learning English vocabulary), I memorized 10,255 items. The time required for creating the database and for repetitions amounted to 41 minutes per day. This corresponds to the acquisition rate of 270 items/year/min. The overall retention was 89.3%, but after excluding the recently memorized items (intervals below 3 weeks) which do not exhibit properly determined E-Factors the retention amounted to 92%. Comparing the SM-0 and SM-2 algorithms one must consider the fact that in the former case the retention was artificially high because of hints the student is given while repeating items of a given page. Items preceding the one in question can easily suggest the correct answer.Therefore the SM-2 algorithm, though not stunning in terms of quantitative comparisons, marked the second major improvement of the SuperMemo method after the introduction of the concept of optimal intervals back in 1985. Separating items previously grouped in pages and introducing E-Factors were the two major components of the improved algorithm. Constructed by means of the trial-and-error approach, the SM-2 algorithm proved in practice the correctness of nearly all basic assumptions that led to its conception.
1988: Two component of memory
Two-component model of long-term memory lays at the foundation of SuperMemo, and is expressed explicitly in Algorithm SM-17. It differentiates between how stable knowledge is in long term memory storage, and how easy it is to retrieve. This remains a little known and quintessential fact of the theory of learning that one can be fluent and still remember poorly.
Fluency is a poor measure of learning in the long term
Components of long-term memory
I first described the idea of two components of memory in a paper for my computer simulations class on Jan 9, 1988. In the same paper, I concluded that different circuits must be involved in declarative and procedural learning.
If you pause for a minute, the whole idea of two components should be pretty obvious. If you take two items right after a review, one with a short optimum interval and the other with a long optimum interval, the memory status of the two must differ. Both can be recalled perfectly (maximum retrievability) and they also need to differ in how long they can last in memory (different stability). I was surprised I could not find any literature on the subject. However, if the literature has no mention of the existence of the optimum interval in spaced repetition, this seemingly obvious conclusion might be hiding behind another seemingly obvious idea: the progression of increasing interval in optimally spaced review. This is a lovely illustration how human progress is incremental and agonizingly slow. We are notoriously bad at thinking out of the box. The darkest place is under the candlestick. This weakness can be broken with an explosion of communication on the web. I advocate less peer review and more bold hypothesizing. I speak of a fantastic example coming from Robin Clarke’s paper in reference to Alzheimer’s. Strict peer review is reminiscent of Prussian schooling: in the quest for perfection, we lose our creativity, then humanity, and ultimately the pleasure of life.
When I first presented my ideas to my teacher Dr Katulski on Feb 19, 1988, he was not too impressed, but he gave me a pass for computer simulations credit. Incidentally, a while later, Katulski became one of the first users of SuperMemo 1.0 for DOS.
In my Master’s Thesis (1990), I added a slightly more formal proof of the existence of the two components. That part of my thesis remained unnoticed.
In 1994, J. Kowalski wrote in Enter, Poland:
We got to the point where the evolutionary interpretation of memory indicates that it works using the principles of increasing intervals and the spacing effect. Is there any proof for this model of memory apart from the evolutionary speculation? In his Doctoral Dissertation, Wozniak discussed widely molecular aspects of memory and has presented a hypothetical model of changes occurring in the synapse in the process of learning. The novel element presented in the thesis was the distinction between the stability and retrievability of memory traces. This could not be used to support the validity of SuperMemo because of the simple fact that it was SuperMemo itself that laid the groundwork for the hypothesis. However, an increasing molecular evidence seems to coincide with the stability-retrievability model providing, at the same time, support for the correctness of assumptions leading to SuperMemo. In plain terms, retrievability is a property of memory which determines the level of efficiency with which synapses can fire in response to the stimulus, and thus elicit the learned action. The lower the retrievability the less you are likely to recall the correct response to a question. On the other hand, stability reflects the history of earlier repetitions and determines the extent of time in which memory traces can be sustained. The higher the stability of memory, the longer it will take for the retrievability to drop to the zero level, i.e. to the level where memories are permanently lost. According to Wozniak, when we learn something for the first time we experience a slight increase in the stability and retrievability in synapses involved in coding the particular stimulus-response association. In time, retrievability declines rapidly; the phenomenon equivalent to forgetting. At the same time, the stability of memory remains at the approximately same level. However, if we repeat the association before retrievability drops to zero, retrievability regains its initial value, while stability increases to a new level, substantially higher than at primary learning. Before the next repetition takes place, due to increased stability, retrievability decreases at a slower pace, and the inter-repetition interval might be much longer before forgetting takes place. Two other important properties of memory should also be noted: (1) repetitions have no power to increase the stability at times when retrievability is high (spacing effect), (2) upon forgetting, stability declines rapidly
We published our ideas with Drs Janusz Murakowski and Edward Gorzelańczyk in 1995. Murakowski perfected the mathematical proof. Gorzelańczyk fleshed out the molecular model. We have not heard much enthusiasm or feedback from the scientific community. The idea of two components of memory is like wine, the older it gets, the better it tastes. We keep wondering when it will receive a wider recognition. After all, we do not live in Mendel‘s time to keep a good gem hidden in some obscure archive. There are millions of users of spaced repetition and even if 0.1% got interested in the theory, they would hear of our two components. Today, even the newest algorithm in SuperMemo is based on the two-component model and it works like a charm. Ironically, users tend to flock to simpler solutions where all the mechanics of human memory remain hidden. Even at supermemo.com we make sure we do not scare customers with excess numbers on the screen.
The concept of the two components of memory has parallels to prior research, esp. by Bjork.
In the 1940s, scientists investigated habit strength and response strength as independent components of behavior in rats. Those concepts were later reformulated in Bjork’s disuse theory. Herbert Simon seems to have noticed the need for memory stability variable in his paper in 1966. In 1969, Robert Bjork formulated the Strength Paradox: a reverse relationship between the probability of recall and the memory effect of a review. Note that his is a restatement of the spacing effect in terms of the two component model, which is just a short step away from formulating the distinction between the variables of memory. This led to Bjork’s New Theory of Disuse (1992) that would distinguish between the storage strength and the retrieval strength. Those are close equivalents of retrievability and stability with a slightly different interpretation of the mechanisms that underlie the distinction. Most strikingly, Bjork believes that when retrievability drops to zero, stable memories are still retained (in our model, stability becomes indeterminate). At the cellular level, Bjork might be right, at least for a while, but practise of SuperMemo shows the power of complete forgetting, while, from the neural point of view, retaining memories in disuse would be highly inefficient independent of their stability. Last but not least, Bjork defines storage strength in terms of connectivity, which is very close to what I believe happens in good students: coherence affects stability.
Why aren’t two components of memory entering mainstream research yet? I claim that if human mind tends to be short-sighted, and we all are, by design, the mind of science can be truly strangulated by strenuous duties, publish or perish, battles for grants, hierarchies, conflict of interest, peer review, teaching obligations and even the code of conduct. Memory researchers tend to live in a single dimension of “memory strength”. In that dimension, they cannot truly appreciate true dynamics of molecular processes that need to be investigated to crack the problem. Ironically, progress may come from those who tend to work in artificial intelligence or neural network. Prodigious minds of Demis Hassabis or Andreas Knoblauch come up with twin ideas by independent reasoning process, models, and simulations. Biologists will need to listen to the language of mathematics or computer science.
Two component model in Algorithm SM-17
The two component model of long-term memory underlies Algorithm SM-17. The success of Algorithm SM-17 is the ultimate practical proof for the correctness of the model.
A graph of actual changes in the value of the two components of memory provides a conceptual visualization of the evolving memory status:
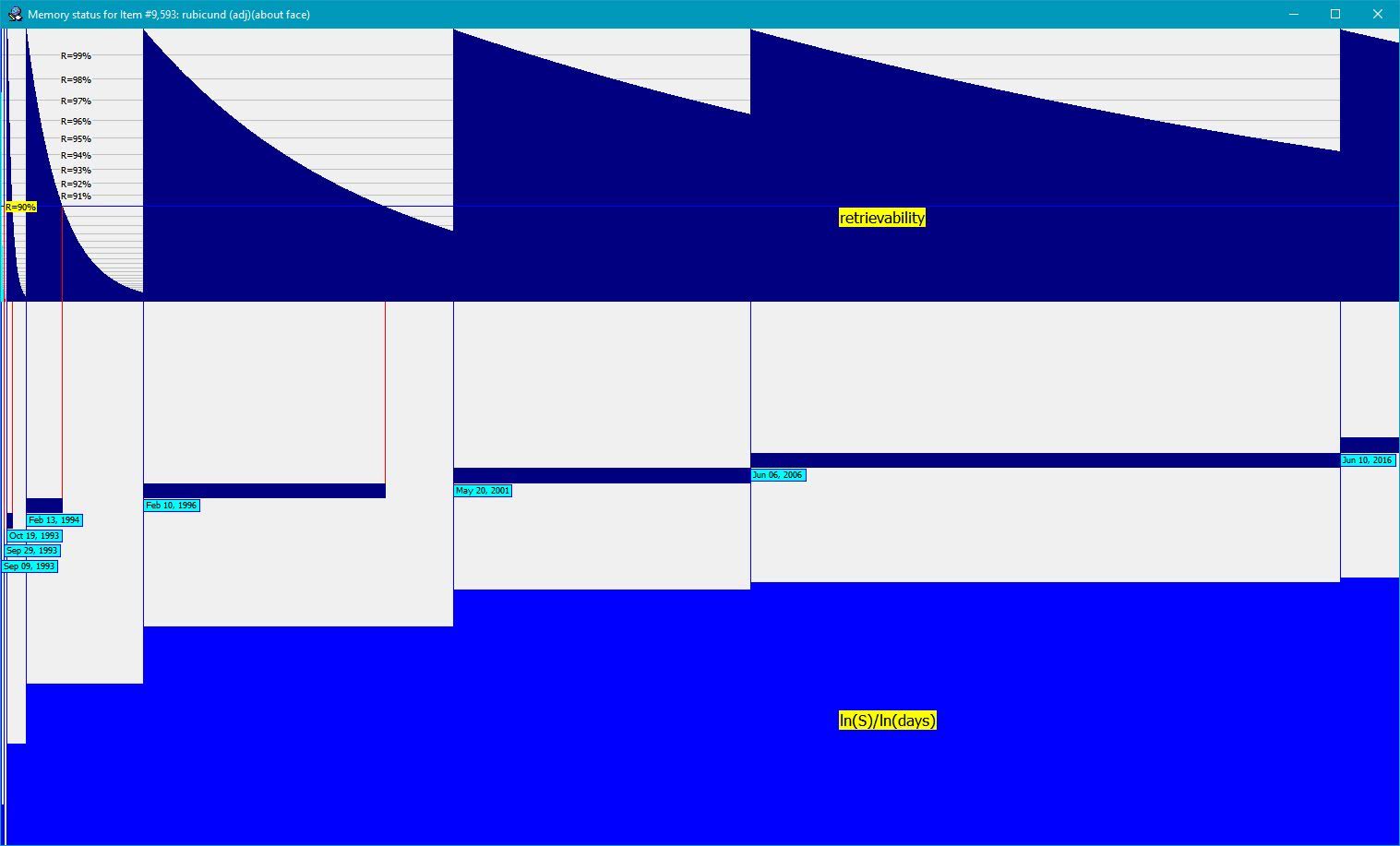
Figure: Changes in memory status over time for an exemplary item. The horizontal axis represents time spanning the entire repetition history. The top panel shows retrievability (tenth power, R^10, for easier analysis). Retrievability grid in gray is labelled by R=99%, R=98%, etc. The middle panel displays optimum intervals in navy. Repetition dates are marked by blue vertical lines and labelled in aqua. The end of the optimum interval where R crosses 90% line is marked by red vertical lines (only if intervals are longer than optimum intervals). The bottom panel visualizes stability (presented as
ln(S)/ln(days)for easier analysis). The graph shows that retrievability drops fast (exponentially) after early repetitions when stability is low, however, it only drops from 100% to 94% in long 10 years after the 7th review. All values are derived from an actual repetition history and the three component model of memory.
Due to the fact that real-life application of SuperMemo requires tackling learning material of varying difficulty, the third variable involved in the model is item difficulty (D). Some of the implications of item difficulty have also been discussed in the above article. In particular, the impact of composite memories with subcomponents of different memory stability (S).
For the purpose of the new algorithm we have defined the three components of memory as follows:
- Memory Stability (S) is defined as the inter-repetition interval that produces average recall probability of 0.9 at review time
- Memory Retrievability (R) is defined as the expected probability of recall at any time on the assumption of negatively exponential forgetting of homogenous learning material with the decay constant determined by memory stability (S)
- Item Difficulty (D) is defined as the maximum possible increase in memory stability (S) at review mapped linearly into 0..1 interval with 0 standing for easiest possible items, and 1 standing for highest difficulty in consideration in SuperMemo (the cut off limit currently stands at stability increase 6x less than the maximum possible)
Proof
The actual proof from my Master’s Thesis follows. For a better take on this proof, see Murakowski proof.
Archive warning: Why use literal archives?
10.4.2. Two variables of memory: stability and retrievability
There is an important conclusion that comes directly from the SuperMemo theory that there are two, and not one, as it is commonly believed, independent variables that describe the conductivity of a synapse and memory in general. To illustrate the case, let us again consider the calpain model of synaptic memory. It is obvious from the model, that its authors assume that only one independent variable is necessary to describe the conductivity of a synapse. Influx of calcium, activity of calpain, degradation of fodrin and number of glutamate receptors are all examples of such a variable. Note that all the mentioned parameters are dependent, i.e. knowing one of them we could calculate all others; obviously only in the case if we were able to construct the relevant formulae. The dependence of the parameters is a direct consequence of causal links between all of them.
However, the process of optimal learning requires exactly two independent variables to describe the state of a synapse at a given moment:
- A variable that plays the role of a clock that measures time between repetitions. Exemplary parameters that can be used here are:
- T e – time that has elapsed since the last repetition (it belongs to the range <0,optimal-interval>),
- T l – time that has to elapse before the next repetition will take place (T l=optimal-interval-T e),
- P f – probability that the synapse will lose the trace of memory during the day in question (it belongs to the range <0,1>).
- A variable that measures the durability of memory. Exemplary parameters that can be used here are:
- I(n+1) – optimal interval that should be used after the next repetition (I(n+1)=I(n)*C where C is a constant greater than three),
- I(n) – current optimal interval,
- n – number of repetitions preceding the moment in question, etc.
Let us now see if the above variables are necessary and sufficient to characterize the state of synapses in the process of time-optimal learning. To show that variables are independent, we will show that none of them can be calculated from the other. Let us notice that the I(n) parameter remains constant during a given inter-repetition interval, while the T e parameter changes from zero to I(n). This shows that there is no function f that satisfies the condition:
T e=f(I(n))
On the other hand, at the moment of subsequent repetitions, T e always equals zero while I(n) has always a different, increasing value. Therefore there is no function g that satisfies the condition:
I(n)=g(T e)
Hence independence of I(n) and T e.
To show that no other variables are necessary in the process of optimal learning, let us notice that at any given time we can compute all the moments of future repetitions using the following algorithm:
- Let there elapse I(n)-T e days.
- Let there be a repetition.
- Let T e be zero and I(n) increase C times.
- Go to 1.
Note that the value of C is a constant characteristic for a given synapse and as such does not change in the process of learning. I will later use the term retrievability to refer to the first of the variables and the term stability to refer to the second one. To justify the choice of the first term, let me notice that we use to think that memories are strong after a learning task and that they fade away afterwards until they become no longer retrievable. This is retrievability that determines the moment at which memories are no longer there. It is also worth mentioning that retrievability was the variable that was tacitly assumed to be the only one needed to describe memory (as in the calpain model). The invisibility of the stability variable resulted from the fact that researchers concentrated their effort on a single learning task and observation of the follow-up changes in synapses, while the importance of stability can be visualized only in the process of repeating the same task many times. To conclude the analysis of memory variables, let us ask the standard question that must be posed in development of any biological model. What is the possible evolutionary advantage that arises from the existence of two variables of memory?
Retrievability and stability are both necessary to code for a process of learning that allows subsequent inter-repetition intervals to increase in length without forgetting. It can be easily demonstrated that such model of learning is best with respect to the survival rate of an individual if we acknowledge the fact that remembering without forgetting would in a short time clog up the memory system which is a finite one. If memory is to be forgetful it must have a means of retaining of these traces that seem to be important for survival. Repetition as a memory strengthening factor is such a means. Let us now consider what is the most suitable timing of the repetitory process. If a given phenomenon is encountered for the n-th time, the probability that it will be encountered for the n+1 time increases and therefore a longer memory retention time seems advantageous. The exact function that describes the best repetitory process depends on the size of memory storage, number of possible phenomena encountered by an individual, and many others. However, the usefulness of increasing intervals required to sustain memory by repetitions is indisputable and so is the evolutionary value of retrievability and stability of memory. One can imagine many situations interfering with this simple picture of the development of memory in the course of evolution. For example, events that were associated with an intense stress should be remembered better. Indeed, this fact was proved in research on the influence of catecholamines on learning. Perhaps, using hormonal stimulation one could improve the performance of a student applying the SuperMemo method.
Interim summary
- Existence of two independent variables necessary to describe the process of optimal learning was postulated. These variables were named retrievability and stability of memory
- Retrievability of memory reflects the lapse of time between repetitions and indicates to what extent memory traces can successfully be used in the process of recall
- Stability of memory reflects the history of repetitions in the process of learning and increases with each stimulation of the synapse. It determines the length of the optimum inter-repetition interval
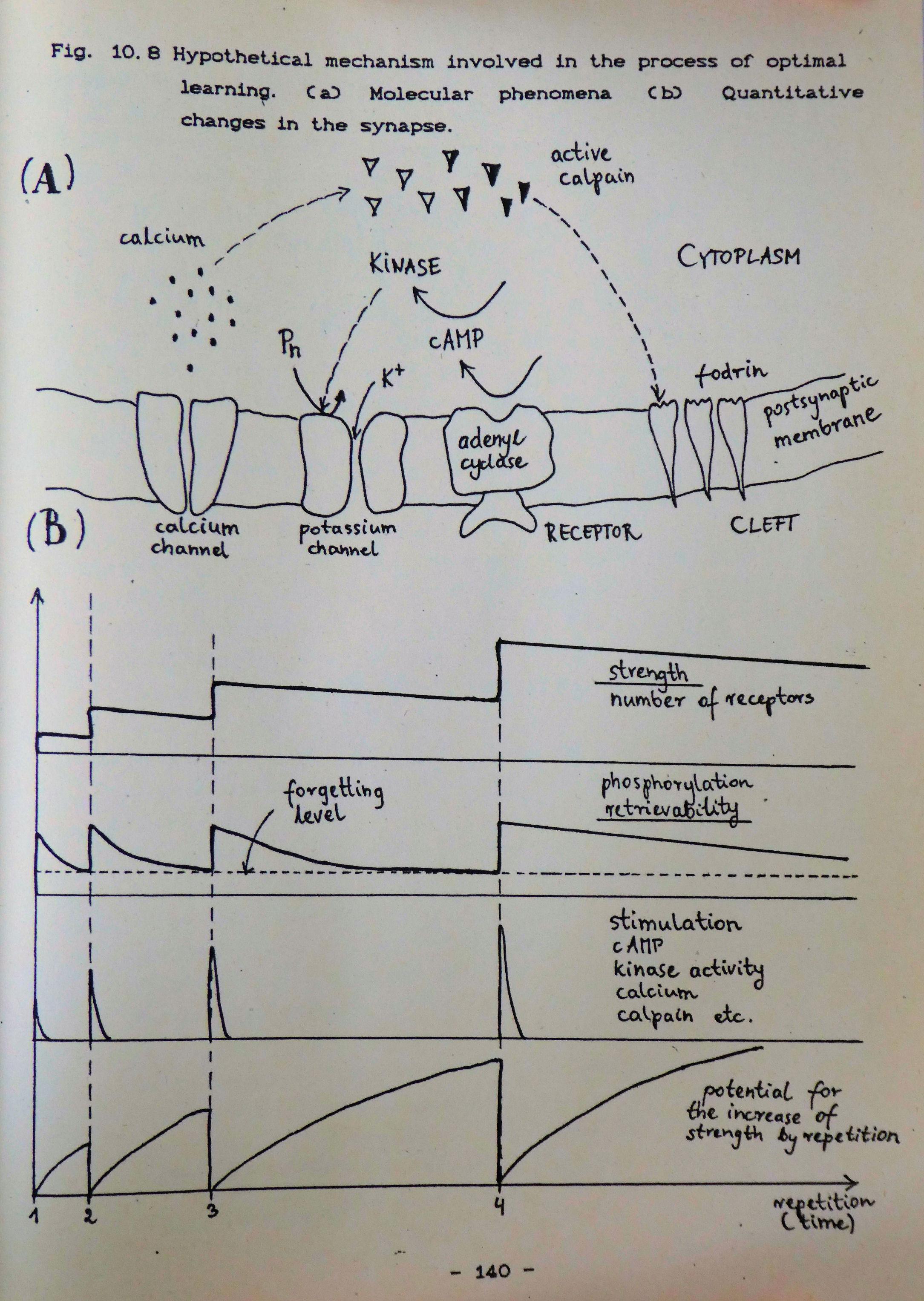
Figure: Hypothetical mechanism involved in the process of optimal learning. (A) Molecular phenomena (B) Quantitative changes in the synapse.
Proof by Murakowski
Here is an improved proof by Murakowski:
It has been found in earlier research that the optimum spacing of repetitions in paired-associate learning, understood as the spacing which takes a minimum number of repetitions to indefinitely maintain a constant level of knowledge retention (e.g. 95%), can roughly be expressed using the following formulae ( Wozniak and Gorzelańczyk 1994).
- (1) I 1=C 1
- (2) I i=I i-1*C 2
where:
- I i – inter-repetition interval after the i-th repetition
- C 1 – length of the first interval (dependent on the chosen knowledge retention, and usually equal to several days)
- C 2 – constant that denotes the increase of inter-repetition intervals in subsequent repetitions (dependent on the chosen knowledge retention, and the difficulty of the remembered item)
The above formulae have been found for human subjects using computer optimization procedures employed to supervise the process of self-paced learning of word-pairs using the active recall drop-out technique. […]
As it will be shown below, the widely investigated strength of memory (or synaptic potentiation) does not suffice to account for the regular pattern of optimum repetition spacing: […]
- We want to determine the set of (molecular) variables involved in storing memory traces that will suffice to account for the optimum spacing of repetitions. Let us, initially, assume two correlates of these variables in learning that is subject to optimum spacing as expressed by Eqns. (1) and (2):r – time which remains from the present moment until the end of the current optimum interval (optimum interval is the interval at the end of which the retention drops to the previously defined level, e.g. 95%)s – length of the current optimum interval.
- Just at the onset of the i-th repetition, r=0, while s i> s i-1>0 ( s i denotes s right at the onset of the i-th repetition). This indicates that there is no function g 1 such that s=g 1( r), i.e. s cannot be a function of r only.
- During the inter-repetition interval, r(t 1)<> r(t 2) if t 1<>t 2 (t denotes time and r(t) denotes r at the moment t). On the other hand, s(t 1)= s(t 2) ( s(t) denotes s at the moment t). This shows that there is no function g 2 such that r=g 2( s), or we would have: r(t 1)=g 2( s(t 1))=g 2 ( s(t 2))= r(t 2), which leads to a contradiction. r cannot be a function of s only.
- In Steps 2 and 3 we have shown that r and s are independent, as there are no functions g 1 and g 2 such that s=g 1( r) or r=g 2( s). This obviously does not mean that there exists no parameter x and functions y s and y r such that s=y s(x) and r=y r(x).
- It can be shown that r and s suffice to compute the optimum spacing of repetitions (cf. Eqns. (1) and (2)). Let us first assume that the two following functions f r and f s are known in the system involved in memory storage: r i=f r( s i) and s i=f s( s i-1). In our case, these functions have a trivial form f r: r i= s i and f s: s i= s i-1*C 2 (where C 2 is the constant from Eqn. (2)). In such a case, the variables r and s are sufficient to represent memory at any moment t in optimum spacing of repetitions. Here is a repetition spacing algorithm which shows this to be true:
- assume that the variables r i and s i describe the state of memory after the i-th repetition
- let there elapse r i time
- let there be a repetition
- let the function f s be used to compute the new value of s i+1 from s i
- let the function f r be used to compute the new value of r i+1 from s i+1
- i:=i+1
- goto 2
The above reasoning shows that variables r and s form a sufficient set of independent variables needed to compute the optimum spacing of repetitions. Obviously, using a set of transformation functions of the form r’’=Tr( r’) and s’’=Ts( s’), one can conceive an infinite family of variable pairs r– s that could describe the status of the memory system. A difficult choice remains to choose such a pair r– s that will most conveniently correspond with molecular phenomena occurring at the level of the synapse.
The following terminology and interpretation is proposed by the authors in a memory system involving the existence of the r– s pair of variables: the variable R, retrievability, determines the probability with which a given memory trace can be invoked at a given moment, while the variable S, stability of memory, determines the rate of decline of retrievability as a result of forgetting, and consequently the length of inter-repetition intervals in the optimum spacing of repetitions.
Assuming the negatively exponential decrease of retrievability, and the interpretation of stability as a reciprocal of the retrievability decay constant, we might conveniently represent the relationship between R and S using the following formula (t denotes time):
(3) R=e -t/S
The transformation functions from the pair r– s used in Steps 1-5 of the reasoning, to the proposed interpretation R-S will look as follows (assuming the definition of the optimum inter-repetition interval as the interval that produces retention of knowledge K=0.95):
(4) S=- s/ln(K)
(5) R=e -( s– r)/S
The relationship between the stability after the i-th repetition (S i) and the constants C 1 and C 2 determining the optimum spacing of repetitions as defined by Eqns. (1) and (2) can therefore be written as:
(6) S i=-(C 1*C 2 i-1)/ln(K)
and finally, retrievability in the optimum spacing of repetitions can be expressed as:
(7) R i(t)=exp (t*ln(K)/(C 1*C 2 i-1))
where:
- i – number of the repetition in question
- t – time since the i-th repetition
- R i(t) – retrievability after the time t passing since the i-th repetition in optimum spacing of repetitions
- C 1 and C 2 – constants from Eqns. (1) and (2)
- K – retention of knowledge equal to 0.95 (it is important to notice that the relationship expressed by Eqn. (7) may not be true for retention higher than 0.95 due to the spacing effect resulting from shorter intervals)
Two components of memory in SuperMemo
SuperMemo has always been based on the two component model, which emerged in an increasingly explicit form over time. The constant C 2 in Eqn. (2) in Murakowski proof above represents stability increase. In 2018, stability increase is represented in SuperMemo as matrix SInc[]. C 2 says how much inter-repetition intervals should increase in learning to meet the criteria of admissible level of forgetting. In reality, C 2 is not a constant. It depends on a number of factors. Of these, the most important are:
- item difficulty (D)(see: complexity): the more difficult the remembered piece of information the smaller the C 2 (i.e. difficult material must be reviewed more often)
- memory stability (S): the more lasting/durable the memory, the smaller the C 2 value
- probability of recall ( retrievability)(R): the lower the probability of recall, the higher the C 2 value (i.e. due to the spacing effect, items are remembered better if reviewed with delay)
Due to those multiple dependencies, the precise value of C 2 is not easily predictable. SuperMemo solves this and similar optimization problems by using multidimensional matrices to represent multi-argument functions and adjusting the value of those matrices on the basis of measurements made during an actual learning process. The initial values of those matrices are derived from a theoretical model or from previous measurements. The actually used values will, over time, differ slightly from those theoretically predicted or those derived from data of previous students.
For example, if the value of C 2 for a given item of a given difficulty with a given memory status produces an inter-repetition interval that is longer than desired (i.e. producing lower than desired level of recall), the value of C 2 is reduced accordingly.
Here is the evolution of stability increase (constant C 2) over years:
- in the paper-and-pencil version of SuperMemo (1985), C 2 was indeed (almost) a constant. Set at the average of 1.75 (varying from 1.5 to 2.0 for rounding errors and simplicity), it did not consider material difficulty, stability or retrievability of memories, etc.
- in early versions of SuperMemo for DOS (1987), C 2, named E-Factor, reflected item difficulty for the first time. It was decreased for bad grades and increased for good grades
- SuperMemo 4 (1989) did not use C 2, but, to compute inter-repetition intervals, it employed optimization matrices for the first time
- in SuperMemo 5 (1990), C 2, named O-Factor was finally represented as a matrix and it included both the difficulty dimension as well as the stability dimension. Again, entries of the matrix would be subject to the measure-verify-correct cycle that would, starting with the initial value based on prior measurements, produce a convergence towards the value that would satisfy the learning criteria
- in SuperMemo 6 (1991), C 2, in the form of the O-Factor matrix would be derived from a three-dimensional matrix that would include the retrievability dimension. The important implication of the third dimension was that, for the first time, SuperMemo would make it possible to inspect forgetting curves for different levels of difficulty and memory stability
- in SuperMemo 8 (1997) through SuperMemo 16, the representation of C 2 would not change much, however, the algorithm used to produce a quick and stable transition from the theoretical to the real set of data would gradually get more and more complex. Most importantly, new SuperMemos make a better use of the retrievability dimension of C 2. Thus, independent of the spacing effect, the student can depart from the initial learning criteria, e.g. to cram before an exam, without introducing noise into the optimization procedure
- in SuperMemo 17 (2016), C 2 finally took the form based on the original two-component model. It is taken from stability increase matrix (SInc) that has three dimensions that represent the three variables that determine the increase in stability: complexity, stability and retrievability. The SInc matrix is filled up with data during learning using a complex algorithm known as Algorithm SM-17. The stability increase matrix can be inspected in SuperMemo 17 with Tools : Memory : 4D Graphs ( Stability tab)
1989: SuperMemo adapts to user memory
Introducing flexible interval function
SuperMemo 2 was great. Its simple algorithm has survived in various mutations to this day in popular apps such as Anki or Mnemosyne. However, the algorithm was dumb in the sense that there was no way of modifying the function of optimum intervals. The findings of 1985 were set in stone. Memory complexity and stability increase were expressed by the same single number: E-factor. It is a bit like using a single lever in a bike to change gears and the direction of driving.
Individual items could adapt the spacing of review by changes to their estimated difficulty. Those changes could compensate for errors in the function of optimum intervals. Even if the algorithm was slow to converge on the optimum, in theory, it was convergent. The main flaw was that, in Algorithm SM-2, new items would not benefit from the experience of old items.
Algorithm SM-2 is not adaptable. New items do not benefit from the experience of old items
Algorithm SM-4 was the first attempt to arm SuperMemo with universal adaptability. It was completed in February 1989. In the end, adaptability was too slow to show up, but inspiration gathered with Algorithm SM-4 was essential for further progress, esp. in understanding the problem of stability-vs-accuracy in spaced repetition. In short, Algorithm SM-4 was too stable to be accurate. This was quickly remedied in Algorithm SM-5 just 7 months later. Here is an excerpt from my Master’s Thesis to explain the details:
Archive warning: Why use literal archives?
This text is part of: ” Optimization of learning ” by Piotr Wozniak (1990)
The main fault of Algorithm SM-2 seems to have been the arbitrary shape of the function of optimal intervals. Although very effective in practice and confirmed by years of experimental repetitions, this function could not claim scientifically proved validity, nor could it detect the overall impact of few day variations of optimal intervals on the learning process. Bearing these flaws in mind I decided to employ routine SuperMemo repetitions in the validation of the function of optimal intervals!
Using optimization procedures like those applied in finding E-Factors I wanted the program to correct the initially proposed function whenever corrections appeared justified.
To achieve this goal, I tabulated the function of optimal intervals.

Figure: Matrix of optimal intervals showed up in SuperMemo 4 in 1989 and survived to this day in SuperMemo 17 with few changes. The picture presents a matrix from SuperMemo 5 and shows a significant departure from original values of the matrix. In SuperMemo 4, adaptations proceeded at much slower pace
Particular entries of the matrix of optimal intervals (later called the OI matrix) were initially taken from the formulas used in Algorithm SM-2.
SuperMemo 4 (February 1989), in which the new solution was implemented, used the OI matrix to determine values of inter-repetition intervals:
I(n):=OI(n,EF)
where:
- I(n) – the n-th inter-repetition interval of a given item (in days),
- EF – E-Factor of the item,
- OI(n,EF) – the entry of the OI matrix corresponding to the n-th repetition and the E-Factor EF.
However, the OI matrix was not fixed once for all. In the course of repetitions, particular entries of the matrix were increased or decreased depending on the grades. For example, if the entry indicated the optimal interval to be X and the used interval was X+Y while the grade after this interval was not lower than four, then the new value of the entry would fall between X and X+Y.
Thus the values of the OI entries in the equilibrium state should settle at the point where the stream of poor-retention items balances the stream of good-retention items in its influence on the matrix.As a consequence, SuperMemo 4 was intended to yield an ultimate definition of the function of optimal intervals.
Rigid SuperMemo 4
It did not take me long to realize that the verification-correction cycle in the new algorithm was too long. It was not much different than running the 1985 eperiment on the computer. To determine decade-long intervals, I needed a decade to pass to test the outcomes of the review. This led to Algorithm SM-5 seven months later. Here is the problem with Algorithm SM-4 as described in my Master’s Thesis:
Archive warning: Why use literal archives?
This text is part of: ” Optimization of learning ” by Piotr Wozniak (1990)
Algorithm SM-4 was implemented in SuperMemo 4 and was used between March 9, 1989 and October 17, 1989. Although the main concept of modifying the function of optimal intervals seemed to be a major step forward, the implementation of the algorithm was a failure. The basic insufficiency of the algorithm appeared to result from formulas applied in modification of the OI matrix.
There were two the most striking flaws:
- modifications were too subtle to rearrange the OI matrix visibly in a reasonably short time,
- for longer inter-repetition intervals, the effect of modification had to wait very long before being steadily fixed, i.e. it took quite a lot of time before the result of a modification of a few-month-long interval could be seen and corrected if necessary
After seven months of using Algorithm SM-4, the OI matrices of particular databases did not look much different from their initial states. One could explain this fact by the correctness of my earlier predictions concerning the real values of the optimal inter-repetition intervals, however, as it was later proved by means of Algorithm SM-5, the actual reason of the stability of the matrices was the flaws in the optimization formulae.As far as acquisition rate and retention are concerned, there is no reliable evidence that Algorithm SM-4 brought any progress. Slight improvement could as well be related to general betterment of the software and improvement in item formulation principles
Remnants of SuperMemo 4 in new SuperMemos
Interestingly, you can still see the matrix of optimum intervals in newer versions of SuperMemo. The matrix is not used by the algorithm, however, it is displayed in SuperMemo statistics as it informs the user about the impact of complexity on the prospects of items in the learning process.
If you compare a matrix produced by SuperMemo 5 in 8 months of use, you will notice significant similarity to a matrix produced in two decades of use of Algorithm SM-8:
Figure: Matrix of optimum intervals is no longer used in Algorithm SM-17. However, it can still be generated with procedures of Algorithm SM-15. The columns correspond with easiness of the material expressed as A-Factor. The rows correspond with memory stability expressed as repetition category
Algorithm SM-4
Here is the outline of Algorithm SM-4 as described in my Master’s Thesis:
Archive warning: Why use literal archives?
This text is part of: ” Optimization of learning ” by Piotr Wozniak (1990)
Algorithm SM-4 used in SuperMemo 4.0:
- Split the knowledge into smallest possible items
- With all items associate an E-Factor equal to 2.5
- Tabulate the OI matrix for various repetition numbers and E-Factor categories
- Use the following repetition spacing to obtain the initial OI matrix:OI(1,EF):=1OI(2,EF):=6for n>2 OI(n,EF):=OI(n-1,EF)*EFwhere:
- OI(n,EF) – optimal inter-repetition interval after the n-th repetition (in days) for items with E-Factor equal EF,
- Use the OI matrix to determine inter-repetition intervals:I(n,EF):=OI(n,EF)where:
- I(n,EF) – the n-th inter-repetition interval for an item whose E-Factor equals EF (in days),
- OI(n,EF) – the entry of the OI matrix corresponding to the n-th repetition and the E-Factor EF
- After each repetition estimate the quality of the repetition response in the 0-5 grade scale (see Algorithm SM-2).
- After each repetition modify the E-Factor of the recently repeated item according to the formula:EF’:=EF+(0.1-(5-q)*(0.08+(5-q)*0.02))where:
- EF’ – new value of the E-Factor,
- EF – old value of the E-Factor,
- q – quality of the response in the 0-5 grade scale.
- After each repetition modify the relevant entry of the OI matrix.
- An exemplary formula could look as follows (the actual formula used in SuperMemo 4 was more intricate):OI’:=interval+interval*(1-1/EF)/2*(0.25*q-1)OI :=(1-fraction)*OI+fraction*OI’where:
- OI – new value of the OI entry,
- OI’ – auxiliary value of the OI entry used in calculations,
- OI – old value of the OI entry,
- interval – interval used before the considered repetition (i.e. the last used interval for the given item),
- fraction – any number between 0 and 1 (the greater it is the faster the changes of the OI matrix),
- EF – E-Factor of the repeated item,
- q – quality of the response in the 0-5 grade scale.
- If the quality response was lower than 3 then start repetitions for the item from the beginning without changing the E-Factor.
- After each repetition session of a given day repeat again all the items that scored below four in the quality assessment. Continue the repetitions until all of these items score at least four
Problems with interval matrix
In addition to slow convergence, Algorithm SM-4 showed that the use of matrix of intervals leads to several problems that could easily be solved by replacing intervals with O-factors. Those additional flaws led to a fast implementation of Algorithm SM-5 yet in 1989. Here is a short analysis that explained the flaws in the use of the matrix of optimum intervals:
Archive warning: Why use literal archives?
This text is part of: ” Optimization of learning ” by Piotr Wozniak (1990)
- In the course of repetition it may happen that one of the intervals will be calculated as shorter than the preceding one. This is certainly inconsistent with general assumptions leading to the SuperMemo method. Moreover, validity of such an outcome was refuted by the results of application of the Algorithm SM-5. This flaw could be prevented by disallowing intervals to increase or drop beyond certain values, but such an approach would tremendously slow down the optimization process interlinking optimal intervals by superfluous dependencies. The discussed case was indeed observed in one of the databases. The discrepancy was not eliminated by the end of the period in which the Algorithm SM-4 was used despite the fact that the intervals in question were only two weeks long
- E-Factors of particular items are constantly modified thus in the OI matrix an item can pass from one difficulty category to another. If the repetition number for that item is large enough, this will result in serious disturbances of the repetitory process of that item. Note that the higher the repetition number, the greater the difference between optimal intervals in neighboring E-Factor category columns. Thus if the E-Factor increases the optimal interval used for the item can be artificially long, while in the opposite situation the interval can be much too short
The Algorithm SM-4 tried to interrelate the length of the optimal interval with the repetition number. This approach seems to be incorrect because the memory is much more likely to be sensitive to the length of the previously applied inter-repetition interval than to the number of the repetition.
SuperMemo 5
The idea of the matrix of optimum intervals was born on Feb 11, 1989. On Mar 1, 1989, I started using SuperMemo 4 to learn Esperanto. Very early I noticed that the idea needs revision. The convergence of the algorithm was excruciatingly slow.
By May 5, I had a new idea in my mind. This was, in essence, the birth of stability increase function, except, in the optimum review of SuperMemo there would be no retrievability dimension. The new algorithm would use the matrix of optimum factors. It would remember how much intervals need to increase depending on memory complexity and current memory stability. Slow convergence of Algorithm SM-4 also inspired the need to randomize intervals (May 20).
In the meantime, progress had to be delayed because of school obligations again. With Krzysztof Biedalak, we decided to write a program for developing school tests that could be used with SuperMemo. The project was again used to wriggle out from other obligations in classes with open-minded Dr Katulski who has become a supporter of all-things SuperMemo by now.
I spent summer on practical training in the Netherlands when progress was slow due to various obligations. One of the chief reasons for slowness was extreme dieting that resulted from the need to save money to pay my PC 1512 debts. I also hoped to earn something extra to buy a hard disk for my computer. All my work was possible thanks to the courtesy of Peter Klijn of the University of Eindhoven. He just gave me his PC for my private use for the whole period of stay. He did not want my good work over SuperMemo to slow down. It was the first time I could keep all my files on a hard disk and it felt like a move from an old bike to Tesla Model S.
Only on Oct 16, 1989, the new Algorithm SM-5 was completed and I started using SuperMemo 5. I remarked in my notes: ” A great revolution is in the offing“. The progress was tremendous indeed.
I had a couple of users of SuperMemo 2 that were ready to upgrade to SuperMemo 5. I demanded only one price: they will start with the matrix of optimum factors initialized to a specific value. This was to validate the algorithm and make sure it carries no preconceived prejudice. All preset optimization matrices would converge nicely and fast. This fact was then used to claim universal convergence and the algorithm was described as such in the first-ever publication about spaced repetition algorithms.
Algorithm SM-5
SuperMemo uses a simple principle: “use, verify, and correct”. After a repetition, a new interval is computed with the help of the OF matrix. The “relevant entry” to compute the interval depends on the repetition (category) and item difficulty. After the interval elapses, SuperMemo calls for the next repetition. The grade is used to tell SuperMemo how well the interval “performed”. If the grade is low, we have reasons to believe that the interval is too long and the OF matrix entry is too high. In such cases, we slightly reduce the OF entry. The relevant entry here is the one that was previously used in computing the interval (i.e. before the interval started). In other words, it is the entry that is (1) used to compute the interval (after n-th repetition) and then (2) used to correct the OF matrix (after the n+1 repetition).
Here is an outline of Algorithm SM-5 as presented in my Master’s Thesis:
Archive warning: Why use literal archives?
The final formulation of the algorithm used in SuperMemo 5 is presented below (Algorithm SM-5):
- Split the knowledge into smallest possible items
- With all items associate an E-Factor equal to 2.5
- Tabulate the OF matrix for various repetition numbers and E-Factor categories. Use the following formula:OF(1,EF):=4for n>1 OF(n,EF):=EFwhere:
- OF(n,EF) – optimal factor corresponding to the n-th repetition and the E-Factor EF
- Use the OF matrix to determine inter-repetition intervals:I(n,EF)=OF(n,EF)*I(n-1,EF)I(1,EF)=OF(1,EF)where:
- I(n,EF) – the n-th inter-repetition interval for an item of a given E-Factor EF (in days)
- OF(n,EF) – the entry of the OF matrix corresponding to the n-th repetition and the E-Factor EF
- After each repetition assess the quality of repetition responses in the 0-5 grade scale (cf. Algorithm SM-2)
- After each repetition modify the E-Factor of the recently repeated item according to the formula:EF’:=EF+(0.1-(5-q)*(0.08+(5-q)*0.02))where:
- EF’ – new value of the E-Factor
- EF – old value of the E-Factor
- q – quality of the response in the 0-5 grade scale
- After each repetition modify the relevant entry of the OF matrix. Exemplary formulas constructed arbitrarily and used in the modification could look like this:OF’:=OF*(0.72+q*0.07)OF :=(1-fraction)*OF+fraction*OF’where:
- OF – new value of the OF entry
- OF’ – auxiliary value of the OF entry used in calculations
- OF – old value of the OF entry
- fraction – any number between 0 and 1 (the greater it is the faster the changes of the OF matrix)
- q – quality of the response in the 0-5 grade scale
- If the quality response was lower than 3 then start repetitions for the item from the beginning without changing the E-Factor
- After each repetition session of a given day repeat again all items that scored below four in the quality assessment. Continue the repetitions until all of these items score at least four
In accordance with the previous observations, the entries of the OF matrix were not allowed to drop below 1.2. In Algorithm SM-5, by definition, intervals cannot get shorter in subsequent repetitions. Intervals are at least 1.2 times as long as their predecessors. Changing the E-Factor category increases the next applied interval only as many times as it is required by the corresponding entry of the OF matrix.
Criticism of Algorithm SM-5
Anki manual includes a passage that is surprisingly critical of Algorithm SM-5 (Apr 2018). The words are particularly surprising as Algorithm SM-5 has never been published in full (the version above is just a rough outline). Despite the fact that the words of criticism were clearly uttered in goodwill, they hint at the possibility that if Algorithm SM-2 was superior over Algorithm SM-5, perhaps it is also superior over Algorithm SM-17. If that was the case, I would have wasted the last 30 years of research and programming. To this day, Wikipedia “criticises” “SM3+”. “SM3+” is a label first used in Anki manual that has been used at dozens of sites on the web (esp. those that prefer to stick with the older algorithm for its simplicity). A comparison between Algorithm SM-2 and Algorithm SM-17 is presented here.
Erroneous claim in Anki manual
My Master’s Thesis published in excerpts in 1998 at supermemo.com included only a rough description of the Algorithm SM-5. For the sake of clarity, dozens of minor procedures were not published. Those procedures would require a lot of tinkering to ensure good convergence, stability, and accuracy. This type of tinkering requires months of learning combined with analysis. There has never been a ready out-of-the box version of Algorithm SM-5.
The source code of Algorithm SM-5 has never been published or opened, and the original algorithm could only be tested by users of SuperMemo 5, in MS DOS. SuperMemo 5 became freeware in 1993. It is important to notice that random dispersal of intervals around the optimum value was essential for establishing convergence. Without the dispersal, the progression of the algorithm would be agonizingly slow. Similarly, matrix smoothing was necessary for consistent behavior independent of the richness of data collected for different levels of stability and item complexity.
Multiple evaluations done in 1989, and since, have pointed to an unquestionable superiority of Algorithm SM-5 and later algorithms over Algorithm SM-2 in any metric studied. Algorithm SM-17 might actually be used to measure the efficiency of Algorithm SM-5 if we had volunteers to re-implement that ancient code for use with our universal metrics. We have done this for Algorithm SM-2 thus far for the implementation cost was insignificant. Needless to say, Algorithm SM-2 lags well behind in its predictive powers, esp. for suboptimum levels of retrievability.
Even a basic understanding of the underlying model should make it clear that a good implementation would yield dramatic benefits. SuperMemo 5 would adapt its function of intervals to the user’s memory. SuperMemo 2 was set in stone. I am very proud that wild guesses made in 1985 and 1987 stood the test of time, but no algorithm should trust the judgment of a humble student with 2 years experience in the implementation of spaced repetition algorithms. Instead, SuperMemo 4 and all successive implementations made fewer and fewer guesses and provided better and faster adaptability. Of all those implementations, only SuperMemo 4 was slow to adapt and was replaced in 7 months by a superior implementation.
There is no ill-will in Anki criticism but I would not be surprised if the author pushed for an implementation and speedy move to self-learning rather than spending time on tinkering with procedures that did not seem to work as he expected. In contrast, back in 1989, I knew Algorithm SM-2 was flawed, I knew Algorithm SM-5 was superior, and I would spare no time and effort in making sure the new concept was perfected to its maximum theoretical potential.
Excerpt from the Anki manual (April 2018):
Anki was originally based on the SuperMemo SM5 algorithm. However, Anki’s default behaviour of revealing the next interval before answering a card revealed some fundamental problems with the SM5 algorithm. The key difference between SM2 and later revisions of the algorithm is this:
- SM2 uses your performance on a card to determine the next time to schedule that card
- SM3+ use your performance on a card to determine the next time to schedule that card, and similar cards
The latter approach promises to choose more accurate intervals by factoring in not just a single card’s performance, but the performance as a group. If you are very consistent in your studies and all cards are of a very similar difficulty, this approach can work quite well. However, once inconsistencies are introduced into the equation (cards of varying difficulty, not studying at the same time every day), SM3+ is more prone to incorrect guesses at the next interval – resulting in cards being scheduled too often or too far in the future.
Furthermore, as SM3+ dynamically adjusts the “optimum factors” table, a situation can often arise where answering “hard” on a card can result in a longer interval than answering “easy” would give. The next times are hidden from you in SuperMemo so the user is never aware of this.After evaluating the alternatives, the Anki author decided that near-optimum intervals yielded by an SM2 derivative are better than trying to obtain optimum intervals at the risk of incorrect guesses. An SM2 approach is predictable and intuitive to end users, whereas an SM3+ approach hides the details from the user and requires users to trust the system (even when the system may make mistakes in the scheduling).
Some details for anyone who cares:
- the fact that SuperMemo 5 used past performance of all items to maximize performance on new items is an advantage, not a “problem”. Even more, that is the key to the power of adaptability
- inconsistent grading has been a problem for all algorithms. On average, adaptability helps find out the average effect of misuse, esp. if inconsistencies are consistent (i.e. user keep committing similar offences in similar circumstances)
- mixed difficulties are handled by SuperMemo 5 much better because while both difficulty and stability increase are coded by E-factor in SuperMemo 2, in SuperMemo 5 and later, those two properties of memory are separated
- interval predictions have been proven superior in SuperMemo 5 and the claim “more prone to incorrect guesses” can only be explained by errors in implementation
- lower grades could bring longer intervals if matrix smoothing is not implemented. That part of the algorithm has only been described verbally in my thesis
- intervals and repetition dates have always been prominently displayed in SuperMemo, even in most simpler implementations (e.g. for handheld devices, smartphones, etc.). Nothing is hidden from the user. Most of all, forgetting index and burden statistics are in full view and make it possible to see if SuperMemo keeps its retention promise and at what cost to workload
Of all the above claims, only one might be true. SuperMemo 2 might indeed be more intuitive. This problem has plagued SuperMemo for years. Each version is more complex, and it is hard to hide some of that complexity from users. We will keep trying though.
Our official response published at supermemopedia.com in 2011 seems pretty accurate today:
Archive warning: Why use literal archives?
It is great that Anki introduces its own innovations while still giving due credit to SuperMemo. It is true that SuperMemo’s Algorithm SM-2 works great as compared with, for example, Leitner system, or SuperMemo on paper. However, the superiority of Algorithm SM-5 over SM-2 is unquestionable. Both in practice and in theory. It is Algorithm SM-2 that has the intervals hard-wired and dependent only on item’s difficulty, which is approximated with a heuristic formula (i.e. a formula based on a guess derived from limited pre-1987 experience). It is true that you cannot “spoil” Algorithm SM-2 by feeding it with false data. It is so only because it is non-adaptable. You probably prefer your word processor with customizable fonts even though you can mess up the text by applying Wingdings.
Algorithm SM-2 simply crudely multiplies intervals by a so-called E-Factor which is a way of expressing item difficulty. In contrast, Algorithm SM-5 collects data about user’s performance and modifies the function of optimum intervals accordingly. In other words, it adapts to the student’s performance. Algorithm SM-6 goes even further and modifies the function of optimum intervals so that to achieve a desired level of knowledge retention. The superiority of those newer algorithms has been verified in more ways than one, for example, by measuring the decline in workload over time in fixed-size databases. In cases studied (small sample), the decline of workload with newer algorithms was nearly twice as fast as compared with older databases processed with Algorithm SM-2 (same type of material: English vocabulary).
All SuperMemo algorithms group items into difficulty categories. Algorithm SM-2 gives each category a rigid set of intervals. Algorithm SM-5 gives each category the same set of intervals too, however, these are adapted on the basis of user’s performance, i.e. not set in stone.
Consistency is indeed more important in Algorithm SM-5 than it is in Algorithm SM-2 as false data will result in “false adaptation”. However, it is always bad to give untrue/cheat grades in SuperMemo, whichever algorithm you use.With incomplete knowledge of memory, adaptability is always superior to rigid models. This is why it is still better to adapt to an imprecise average (as in Algorithm SM-5) than to base the intervals on an imprecise guess (as in Algorithm SM-2). Needless to say, the last word goes to Algorithm SM-8 and later, as it adapts to the measured average.
Evaluation of SuperMemo 5 (1989)
SuperMemo 5 was so obviously superior that I did not collect much data to prove my point. I made only a few comparisons for my Master’s Thesis and they left no doubt.
Archive warning: Why use literal archives?
3.8. Evaluation of the Algorithm SM-5
The Algorithm SM-5 has been in use since October 17, 1989 and has surpassed all expectations in providing an efficient method of determining the desired function of optimal intervals, and in consequence, improving the acquisition rate (15,000 items learnt within 9 months). Fig. 3.5 indicates that the acquisition rate was at least twice as high as that indicated by combined application of the SM-2 and SM-4 algorithms!
Figure: Changes of the work burden in databases supervised by SM-2 and SM-5 algorithms.
The knowledge retention increased to about 96% for 10-month-old databases. Below, some knowledge retention data in selected databases are listed to show the comparison between the SM-2 and SM-5 algorithms:
- Date – date of the measurement,
- Database – name of the database; ALL means all databases averaged
- Interval – average current interval used by items in the database
- Retention – knowledge retention in the database
- Version – version of the algorithm applied to the database
| Date | Database | Interval | Retention | Version |
|---|---|---|---|---|
| Dec 88 | EVD | 17 days | 81% | SM-2 |
| Dec 89 | EVG | 19 days | 82% | SM-5 |
| Dec 88 | EVC | 41 days | 95% | SM-2 |
| Dec 89 | EVF | 47 days | 95% | SM-5 |
| Dec 88 | all | 86 days | 89% | SM-2 |
| Dec 89 | all | 190 days | 92% | SM-2, SM-4 and SM-5 |
In the process of repetition the following distribution of grades was recorded:
| Quality | Fraction |
|---|---|
| 0 | 0% |
| 1 | 0% |
| 2 | 11% |
| 3 | 18% |
| 4 | 26% |
| 5 | 45% |
This distribution, in accordance to the assumptions underlying the Algorithm SM-5, yields the average response quality equal 4. The forgetting index equals 11% (items with quality lower than 3 are regarded as forgotten). Note, that the retention data indicate that only 4% of items in a database are not remembered. Therefore forgetting index exceeds the percentage of forgotten items 2.7 times.In a 7-month old database, it was found that 70% of items had not been forgotten even once in the course of repetitions preceding the measurement, while only 2% of items had been forgotten more than 3 times.
Theoretic proof of superiority of newer algorithms
Anki’s criticism of SuperMemo 5 calls for a simple proof in the light of modern spaced repetition theory. We can show that today’s model of memory can be mapped onto the models underlying both algorithms: Algorithm SM-2 and Algorithm SM-5, and the key difference between the two is the missing adaptability of the function of optimal intervals (represented in Algorithm SM-5 as Matrix OF).
Let SInc=f(C,S,R) be a stability increase function that takes complexity C, stability S, and retrievability R as arguments. This function determines the progressive increase in review intervals in optimum learning.
Both Algorithms, SM-2 and SM-5 ignore the retrievability dimension. In theory, if both algorithms worked perfectly, we could assume they aim at R=0.9. As it can be measured in SuperMemo, both algorithms fail at that effort for they do not know relevant forgetting curves. They simply do not collect forgetting curve data. This function was introduced only in Algorithm SM-6 in 1991.
However, if we assume that 1985 and 1987 heuristics were perfect guesses, in theory, the algorithm could use SInc=F(C,S) with constant R of 90%.
Due to the fact that SM-2 uses the same number, EF for stability increase and for item complexity, for SM-2 we have SInc=f(C,S) equation represented by EF=f'(EF,interval), where it can be shown easily with data that f<>f’. Amazingly, the heuristic used in SM-2 made this function work by decoupling the actual link between the EF and item complexity. As data shows that SInc keeps decreasing with S, this means that in Algorithm SM-2, by definition, all items would need to gain on complexity with each review if EF was to represent item complexity. In practical terms, Algorithm SM-2 uses EF=f'(EF,interval), which translates to SInc(n)=f(SInc(n-1),interval).
Let us assume that the EF=f(EF,interval) heuristic was an excellent guess as claimed by users of Algorithm SM-2. Let SInc be represented by O-factor in Algorithm SM-5. We might then represent SInc=f(C,S) as OF=f(EF,interval).
For Algorithm SM-2, OF would be constant and equal to EF, in Algorithm SM-5, OF is adaptable and can be modified depending on algorithm’s performance. It seems pretty obvious that penalizing the algorithm for bad performance by a drop to OF matrix entries and rewarding it by an increase in OF entries is superior to keeping OF constant.
On a funny twist, as much as supporters of Algorithm SM-2 claim it performs great, supporters of neural network SuperMemo kept accusing algebraic algorithms of: lack of adaptability. In reality, the adaptability of Algorithm SM-17 is best to-date as it is based on the most accurate model of memory.
It is conceivable that heuristics used in SM-2 were so accurate that the original guess on OF=f(EF,interval) needed no modification. However, as it has been shown in practical application, the matrix OF quickly evolves and converges onto values described in Wozniak, Gorzelańczyk 1994. They differ substantively from the assumption wired into Algorithm SM-2.
Summary:
- today: SInc=f(C,S,R), 3 variables, f is adaptable
- sm5: SInc=f(C,S,0.9), 2 variables, f is adaptable
- sm2: SInc=f(SInc,S,0.9) – 1 variable, f is fixed
Convergence
Algorithm SM-5 showed fast convergence, which was quickly demonstrated by users who began with univalent OF matrices. It was quite a contrast with Algorithm SM-4.
Archive warning: Why use literal archives?
3.6. Improving the predetermined matrix of optimal factors
The optimization procedures applied in transformations of the OF matrix appeared to be satisfactorily efficient resulting in fast convergence of the OF entries to their final values.
However, in the period considered (Oct 17, 1989 – May 23, 1990) only those optimal factors which were characterized by short modification-verification cycles (less than 3-4 months) seem to have reached their equilibrial values.
It will take few further years before more sound conclusions can be drawn regarding the ultimate shape of the OF matrix. The most interesting fact apparent after analyzing 7-month-old OF matrices is that the first inter-repetition interval should be as long as 5 days for E-Factor equal 2.5 and even 8 days for E-Factor equal 1.3! For the second interval the corresponding values were about 3 and 2 weeks respectively.
The newly-obtained function of optimal intervals could be formulated as follows:
I(1)=8-(EF-1.3)/(2.5-1.3)*3
I(2)=13+(EF-1.3)/(2.5-1.3)*8
for i>2 I(i)=I(i-1)*(EF-0.1)
where:
- I(i) – interval after the i-th repetition (in days)
- EF – E-Factor of the considered item.
To accelerate the optimization process, this new function should be used to determine the initial state of the OF matrix (Step 3 of the SM-5 algorithm). Except for the first interval, this new function does not differ significantly from the one employed in Algorithms SM-0 through SM-5. One could attribute this fact to inefficiencies of the optimization procedures which, after all, are prejudiced by the fact of applying a predetermined OF matrix. To make sure that it is not the fact, I asked three of my colleagues to use experimental versions of the SuperMemo 5.3 in which univalent OF matrices were used (all entries equal to 1.5 in two experiments and 2.0 in the remaining experiment).Although the experimental databases have been in use for only 2-4 months, the OF matrices seem to slowly converge to the form obtained with the use of the predetermined OF matrix. However, the predetermined OF matrices inherit the artificial correlation between E-Factors and the values of OF entries in the relevant E-Factor category (i.e. for n>3 the value OF(n,EF) is close to EF). This phenomenon does not appear in univalent matrices which tend to adjust the OF matrices more closely to requirements posed by such arbitrarily chosen elements of the algorithm as initial value of E-Factors (always 2.5), function modifying E-Factors after repetitions etc.
Matrix smoothing
Some of the criticism from the author of Anki might have been a result of not employing matrix smoothing that was an important component of the algorithm and is still used in Algorithm SM-17.
Archive warning: Why use literal archives?
3.7. Propagation of changes across the matrix of optimal factors
Having noticed the earlier mentioned regularities in relationships between entries of the OF matrix I decided to accelerate the optimization process by propagation of modifications across the matrix. If an optimal factor increases or decreases then we could conclude that the OF factor that corresponds to the higher repetition number should also increase.
This follows from the relationship OF(i,EF)=OF(i+1,EF), which is roughly valid for all E-Factors and i>2. Similarly, we can consider desirable changes of factors if we remember that for i>2 we have OF(i,EF’)=OF(i,EF )*EF’/EF (esp. if EF’ and EF are close enough). I used the propagation of changes only across the OF matrix that had not yet been modified by repetition feed-back. This proved particularly successful in case of univalent OF matrices applied in the experimental versions of SuperMemo mentioned in the previous paragraph.
The proposed propagation scheme can be summarized as this:
- After executing Step 7 of the Algorithm SM-5 locate all neighboring entries of the OF matrix that has not yet been modified in the course of repetitions, i.e. entries that did not enter the modification-verification cycle. Neighboring entries are understood here as those that correspond to the repetition number +/- 1 and the E-Factor category +/- 1 (i.e. E-Factor +/- 0.1)
- Modify the neighboring entries whenever one of the following relations does not hold:
- for i>2 OF(i,EF)=OF(i+1,EF) for all EFs
- for i>2 OF(i,EF’)=OF(i,EF )*EF’/EF
- for i=1 OF(i,EF’)=OF(i,EF )
- For all the entries modified in Step 2 repeat the whole procedure locating their yet unmodified neighbors.
Propagation of changes seems to be inevitable if one remembers that the function of optimal intervals depends on such parameters as:
- student’s capacity
- student’s self-assessment habits (the response quality is given according to the student’s subjective opinion)
- character of the memorized knowledge etc.
Therefore it is impossible to provide an ideal, predetermined OF matrix that would dispense with the use of the modification-verification process and, to a lesser degree, propagation schemes.
Random dispersal of intervals
One of the key improvements in Algorithm SM-5 was random dispersal of intervals. On one hand, it dramatically accelerated the optimization process, on the other, it caused a great deal of confusion in users of nearly all future versions of SuperMemo: “why do the same items with the same grade use a different interval at each try?”. Minor deviations are precious. This was laid bare when “naked” Algorithm SM-17 was released in early SuperMemo 17. It could be seen that users who keep a lot of leeches in their collections would easily hit “local minima” from which they could never get out. The random dispersion was restored with some delay. The period of “nakedness” was needed for accurate observations of the algorithm, esp. in multi-decade learning process like my own.
Archive warning: Why use literal archives?
3.5. Random dispersal of optimal intervals
To improve the optimization process further, a mechanism was introduced that may seem to contradict the principle of optimal repetition spacing. Let us reconsider a significant fault of the Algorithm SM-5: A modification of an optimal factor can be verified for its correctness only after the following conditions are met:
- the modified factor is used in calculation of an inter-repetition interval
- the calculated interval elapses and a repetition is done yielding the response quality which possibly indicates the need to increase or decrease the optimal factor
This means that even a great number of instances used in modification of an optimal factor will not change it significantly until the newly calculated value is used in determination of new intervals and verified after their elapse.
The process of verification of modified optimal factors after the period necessary to apply them in repetitions will later be called the modification-verification cycle. The greater the repetition number the longer the modification-verification cycle and the greater the slow-down in the optimization process.
To illustrate the problem of modification constraint let us consider calculations from Fig. 3.4.
One can easily conclude that for the variable INTERVAL_USED greater than 20 the value of MOD5 will be equal 1.05 if the QUALITY equals 5. As the QUALITY=5, the MODIFIER will equal MOD5, i.e. 1.05. Hence the newly proposed value of the optimal factor (NEW_OF) can only be 5% greater than the previous one (NEW_OF:=USED_OF*MODIFIER). Therefore the modified optimal factor will never reach beyond the 5% limit unless the USED_OF increases, which is equivalent to applying the modified optimal factor in calculation of inter-repetition intervals.
Bearing these facts in mind I decided to let inter-repetition intervals differ from the optimal ones in certain cases to circumvent the constraint imposed by a modification-verification cycle.
I will call the process of random modification of optimal intervals dispersal.
If a little fraction of intervals is allowed to be shorter or longer than it should follow from the OF matrix then these deviant intervals can accelerate the changes of optimal factors by letting them drop or increase beyond the limits of the mechanism presented in Fig. 3.4. In other words, when the value of an optimal factor is much different from the desired one then its accidental change caused by deviant intervals shall not be leveled by the stream of standard repetitions because the response qualities will rather promote the change than act against it.
Another advantage of using intervals distributed round the optimal ones is elimination of a problem which often was a matter of complaints voiced by SuperMemo users – the lumpiness of repetition schedule. By the lumpiness of repetition schedule I mean accumulation of repetitory work in certain days while neighboring days remain relatively unburdened. This is caused by the fact that students often memorize a great number of items in a single session and these items tend to stick together in the following months being separated only on the base of their E-Factors.
Dispersal of intervals round the optimal ones eliminates the problem of lumpiness. Let us now consider formulas that were applied by the latest SuperMemo software in dispersal of intervals in proximity of the optimal value. Inter-repetition intervals that are slightly different from those which are considered optimal (according to the OF matrix) will be called near-optimal intervals. The near-optimal intervals will be calculated according to the following formula:
NOI=PI+(OI-PI)*(1+m)
where:
- NOI – near-optimal interval
- PI – previous interval used
- OI – optimal interval calculated from the OF matrix (cf. Algorithm SM-5)
- m – a number belonging to the range <-0.5,0.5> (see below)
or using the OF value:
NOI=PI*(1+(OF-1)*(1+m))
The modifier m will determine the degree of deviation from the optimal interval (maximum deviation for m=-0.5 or m=0.5 values and no deviation at all for m=0).
In order to find a compromise between accelerated optimization and elimination of lumpiness on one hand (both require strongly dispersed repetition spacing) and the high retention on the other (strict application of optimal intervals required) the modifier m should have a near-zero value in most cases.
The following formulas were used to determine the distribution function of the modifier m:
- the probability of choosing a modifier in the range <0,0.5> should equal 0.5:integral from 0 to 0.5 of f(x)dx=0.5
- the probability of choosing a modifier m=0 was assumed to be hundred times greater than the probability of choosing m=0.5:f(0)/f(0.5)=100
- the probability density function was assumed to have a negative exponential form with parameters a and b to be found on the base of the two previous equations:f=a*exp(-b*x)
The above formulas yield values a=0.04652 and b=0.09210 for m expressed in percent.
From the distribution function
integral from -m to m of a*exp(-b*abs(x))dx = P (P denotes probability)
we can obtain the value of the modifier m (for m>=0):
m=-ln(1-b/a*P)/b
Thus the final procedure to calculate the near-optimal interval looks like this:
a:=0.047;
b:=0.092;
p:=random-0.5;
m:=-1/b*ln(1-b/a*abs(p));
m:=m*sgn(p);
NOI:=PI*(1+(OF-1)*(100+m)/100);
where:
- random – function yielding values from the range <0,1) with a uniform distribution of probability
- NOI – near-optimal interval
- PI – previously used interval
- OF – pertinent entry of the OF matrix
1990: Universal formula for memory
Optimum review vs. intermittent review
By 1990, I had no doubt. I had a major discovery at hands. I cracked the problem of forgetting. I knew the optimum timing of review for simple memories. Once I secured the permission to describe my findings in my Master’s Thesis, my appetite for discovery kept growing. I hoped I might find a universal formula for long-term memory. A formula that would help me track the behavior of memory for any pattern of exposure or retrieval.
I already had a collection of data that might help me find the formula. Before discovering the optimum spacing of repetitions in 1985, I used pages of questions for review of knowledge. The review was chaotic and determined by the availability of time, the need, or the mood. I called that ” intermittent learning“. I had recall data for individual pages and for each review. That was the ideal kind of data that did not have the periodicity of SuperMemo. The exact kind of data needed to solve the problem of memory. However, I had that data on paper only.
In Spring 1990, I recruited my sister to do the typing. No. I do not have a younger sister who would do that eagerly. My sister was 17 years my senior. Being a bit inconsiderate for her time, I used her love to make her do the donkey work. I feel guilty about it. She died just two years later. I never had a chance to repay her contribution to the theory of spaced repetition, which she never even had a chance to understand. Starting on May 1, 1990, she used my time away from the computer to transfer the data from paper to the computer. It took her many days of slow typing. It was worth it.
Model of intermittent learning
Throughout the summer of 1990, instead of focusing on my Master’s Thesis, I worked on the ” model of intermittent learning“. It was not unusual for me to work for 10 hours straight, or go to sleep at 7 am empty-handed, or leave the computer churning the numbers overnight.
Persistence and tinkering pay. Only teens can afford it and should be given the space and the freedom. Despite being 28 years old, I was being tolerated at home pretty well. Like an immature teen. I lived at my sister’s apartment where I could leech on her kindness. Long hours at the computer were excused as ” working on my Master’s Thesis“. The truth was nobody asked me to do it, nobody demanded it, it did not even push SuperMemo much ahead. It was a sheer case of scientific curiosity. I just wanted to know how memory works.
I had dozens of pages of questions and their repetition history. I tried to predict “memory lapses per page”. I used root-mean-square deviation for lapse prediction (denoted below as Dev
). By Jul 10, 1990, Tuesday, I reached Dev<3 and felt like the problem was almost “solved.” On Jul 12, 1990, I improved to Dev=2.877 (incidentally, my Thesis speaks of 2.887241). However, by Aug 27, 1990, I declared the problem unsolvable. My notes from that day say:
Personal anecdote. Why use anecdotes?
Aug 27, 1990: I solved the problem of intermittent learning showing that it is unsolvable! One parameter is not able to describe the strength of memory related to the whole page of items. This shows that there are no optimal intervals for items with low E-factors !
On Aug 30 1990, I decribed the model for my Master’s Thesis. The text covered 15 pages that don’t make for a good reading. I bet nobody has ever had the patience to read this all. That chapter has not even been published at supermemo.com when my Master’s Thesis was put on-line in excerpts in the late 1990s.
However, the conclusions drawn on the basis of the model had a profound effect on my thinking about memory in the decades that followed. The whole idea behind the model is actually reminiscent of the optimizations used to deliver Algorithm SM-17 (2014-2016).
When I declared the problem unsolvable, I meant that I could not accurately describe the memory of “difficult pages” as heterogenous materials require more complex models. However, Aug 31, 1990 notes sound far more optimistic:
Personal anecdote. Why use anecdotes?
Aug 31, 1990: Non-stop work on the intermittent learning model. By night, the computer did not manage to get me closer to the solution. However, I had a great idea to calculate optimal intervals using the record-breaking function of the IL model. When I saw the results on the screen I could not believe my [bleep] eyes. These were exactly the same intervals, which I found in 1985 while trying to formulate the SuperMemo method. I was happy like a dog with two tails jumping around the house. So I can say that I really solved the IL problem (compare August 27, 1990). But this success was not everything I was given to discover today. I found that:
- optimal factors decrease with successive intervals (previously I had an intuition that it is so),
- for the forgetting index equal 10% the retention is 94% (as in the EVF database)
- retention is in a linear relation to the forgetting index [comment 2018: in a small range for heterogeneous material] (this could not be calculated from my simulation experiments carried in January)
- the model says that the desirable value of the forgetting index is 5-10% (workload-retention trade-off)
- strength of memory increases most if the interval is twice as long as the optimal one!!!
- the strength of memory increases most if the forgetting index is 20%.
[…] my formulas work only when intervals are not much shorter than the previous strength.
Past (1990) vs. Present (2018)
Conclusions at the end of the chapter and the procedure itself are reminiscent of the methodology I used in 2005 when looking for the universal formula for memory stability increase and then, in 2014, when Algorithm SM-17 was based on a far more accurate mathematical description of memory. Like the newest SuperMemo algorithm, the model made it possible to compute retention for any repetition schedule. Naturally, it was far less accurate as it was based on inferior data. Moreover, what SuperMemo 17 does in real time, it took many hours of computations back in 1990.
This old seemingly boring portion of my Master’s Thesis has then grown in importance by now. I dare say that only inferior data separated that work from Algorithm SM-17 that emerged long 25 years later. I quote the text with minor notational and stylistic improvements without the chapter on forgetting curves that was erroneous due to highly heterogeneous material used in computations:
Archive warning: Why use literal archives?
This text is part of: ” Optimization of learning ” by Piotr Wozniak (1990)
Model of intermittent learning
The SuperMemo model provides a basis for the calculation of optimal intervals that should separate repetitions in the process of time optimal learning.
However, it does not allow to predict the changes of memory variables if repetitions are done in irregular intervals.
Below I present an attempt to augment the SuperMemo model so that it can be used in the description of the process of intermittent learning.
In Chapter 3, I mentioned the way in which I had learnt English and biology before the SM-0 algorithm was developed.
Data collected during that time (1982-1984) provide an excellent basis for the construction of the model of intermittent learning. Items, formulated in compliance with the minimum information principle (usually having the form of pairs of words) were grouped in pages subject to the irregular repetitory process.The collected data, available in the computer readable form, include the description of repetitions of 71 pages, and in addition, 80 similar pages participating in a process supervised by the SM-0 schedule.
Similarity to Algorithm SM-17
Note that the formulation of the problem is reminiscent of the procedure used to compute the stability increase matrix (SInc[]) in Algorithm SM-17. Memory stability was rescaled to make it possible to interpret it as an interval. Even the symbols are similar: S and deviation D, and page lapses substituting for R.
I loved playing with various optimization algorithms. You can still visually observe in SuperMemo 17 how the algorithm runs surface fitting optimizations (see picture). Doing it with 12 variables might have been a bit inefficient, but I never cared about the method as long as I got interesting results that provided new insights into how memory works.
For those familiar with Algorithm SM-17, we changed the notation in the text below. In addition, symbols such as In and Ln in print could easily be misread as logarithms.
The list of changes:
- Ln -> Laps n
- In -> Int n
- Dn -> Dev n
- R -> RepNo
Formulation of the problem of intermittent learning
Archive warning: Why use literal archives?
11.1. Formulation of the problem of intermittent learning
- There are 161 pages.
- Each page contains about 40 items.
- For each page, the description of the learning process (collected during experimental repetitions) has the following form:
- Int i – inter-repetition interval used before the i-th repetition (it ranges from 1 to 800),
- Laps i – number of lapses of memory during the i-th repetition (it ranges from 0 to 40),
- n – total number of repetitions (it ranges from 3 to 20).
- Find the functions f and g described by the formulas:
- S(n) – any variable corresponding to the strength of memory after the n-th repetition (compare Chapter 10),
- Int n – interval used before the n-th repetition; taken from data collected during intermittent learning,
- Laps n – number of memory lapses in the n-th repetition; taken from data collected during intermittent learning,
- Laps(n) – estimation of the number of memory lapses in the n-th repetition (it should correspond with Laps n)
- S1 – a constant,
- Dev – function that describes the difference between values yielded by the functions f and g, and values collected during intermittent learning (it reflects the difference between experimental and theoretically predicted data)
- RepNo – total number of repetitions recorded on all pages
- Dev i – component of the function Dev describing the deviation for the i-th page,
- Laps(j) – number of lapses calculated for the i-th page and j-th repetition using the functions f and g,
- Laps j – number of lapses of memory for the i-th page and j-th repetition; taken from data collected during intermittent learning,
- sqrt(x) – square root of x,
- sqr(x) – second power of x.
Note that functions f and g will provide a basis for valuable biological considerations only if they are simple and defined by a limited number of parameters (e.g. a*ln()+b or a*exp()+b etc.). Otherwise, one could always construct a gigantic, meaningless formula to automatically put Dev to zero.
Solution to the problem of intermittent learning
Archive warning: Why use literal archives?
11.2. Solution to the problem of intermittent learning
In the search for functions f and g that minimize the value of Dev I used a numerical minimization procedure described in Wozniak, 1988b [ A new algorithm for finding local maxima of a function within the feasible region. Credit paper ].
Exemplary functions used in the search could look as follows:
S(1)=x[1]
S(n)=x[2]*Int n*exp(-Laps n*x[3])+x[4])
Laps(n)=x[5]*(1-exp(-Int n/S(n-1)))
where:
- x[i] – variables that are computed by the minimization procedure,
- S(n), Laps(n), Laps n and Int n – as defined in 11.1.
Note, that the function f describing S(n) does not use S(n-1) as its argument (the formulation of the problem allows, but does not require, that the new strength be calculated on the base of the previous strength).
In order to retain simplicity and save time, I set a limit of 12 variables used in the process of minimization.
I tested a great gamut of mathematical functions constructed in accordance with obvious intuitions concerning memory (e.g. that with time passing by, the number of lapses of memory will increase).
These included exponential, logarithmic, power, hyperbolic, sigmoidal, bell-shaped, polynomial and reasonable combinations thereof.
In most cases, the minimization procedure reduced the value of Dev to less than 3, and functions f and g assumed similar shape independent of their nature.
The lowest value of Dev obtained with the use of fewer than 12 variables was 2.887241.
The functions f and g were as follows:
constant S(1)=0.2104031;
function Sn(Intn,Lapsn,S(n-1));
begin
S(n):=0.4584914*(Intn+1.47)*exp(-0.1549229*Lapsn-0.5854939)+0.35;
if Lapsn=0 then
if S(n-1)>In then
S(n):=S(n-1)*0.724994
else
S(n):=Intn*1.1428571;
end;
function Lapsn(Intn,S(n-1));
var quot;
begin
quot:=(Intn-0.16)/(S(n-1)-0.02)+1.652668;
Lapsn:=-0.0005408*quot*quot+0.2196902*quot+0.311335;
end;Without significantly changing the value of Dev, these functions can be easily converted to the following form:
S(1)=1
for Int n>S(n-1): S(n)=1.5*Int n*exp(-0.15*Laps n)+1
Laps(n)=Int n/S(n-1)
Note that:
- particular elements of the function where dropped or rounded whenever the operation did not considerably affect the value of Dev,
- strength was rescaled to allow it to be interpreted as an interval for which the number of lapses equals 1 and the forgetting index equals 2.5% (there are 40 items on a page and 1/40=2.5%),
- the formula for strength can only be valid if Int n is not much less than S(n-1). This is because of the fact that the value S(n-1) must be used in calculation of S(n) if the number of lapses is low, e.g. for Int n<=S(n-1): S(n)=S(n-1)*(1+0.5/(1-exp(S(n-1))*(1-exp(-Int n)))
The function g intentionally did not involve S(n-1) to avoid recursive accumulation of errors in calculations for successive repetitions (note, that the formula used does not consider the history of the process),
- the formulas cannot be used to describe any process in which intervals are manifold longer than the optimal ones. This is because of the fact that for Int n->? the value of Laps(n) exceeds 100%,
- the formulas describe learning of collective items characterized by more or less uniform distribution of E-Factors. Therefore it cannot be used universally for items of variable difficulty.
As for now, the above formulas make up the best description of the process of intermittent learning, and will later be referred to as the model of intermittent learning (IL model for short).
Simulations based on the model of intermittent learning
With the formula found above, I could run a whole series of simulation experiments that would help me answer many hypothetical scenarios on the behavior of memory in various circumstances. Those simulations shaped the progress of SuperMemo for many years to follow. In particular, the trade-off between workload and retention played a major role in optimization of learning as of SuperMemo 6 (1991). Until this day, it is the forgetting index (or retrievability) that provide the guiding criterion in learning, not the intuitively natural increase in memory stability that may occur at lower levels of recall. Set level of memory lapses played the role of the forgetting index below.
Archive warning: Why use literal archives?
11.4. Verification of the model of intermittent learning
To verify the consistency of the model of intermittent learning with the SuperMemo theory, let us try to calculate optimal intervals that should separate repetitions.
The optimal interval will be determined by the moment at which the number of lapses reaches a selected value Laps o.
The algorithm proceeds as follows:
- i:=1
- S(i):=1
- Find Int(i+1) such that Laps(i+1) equals Laps o. Use the formula:
Int(n)=Laps o*S(n-1) (taken from IL model)
where:Int(n) denotes the n-1 optimal interval. - i:=i+1
- S(i):=1.5*Int(i)*exp(-0.15*Laps o)+1 (taken from the IL model)
- goto 3
If Laps o equals 2.5 ( forgetting index 6.25%) and the exact variant of the model of intermittent learning is used then an amazing correspondence can be observed (compare the experiment presented on page 16, Chapter 3.1):
- Rep – number of the repetition
- Interval – optimal interval preceding the repetition, determined by Laps o=2.5 on the base of the IL model,
- Factor – optimal factor equal to the quotient of the optimal interval and previously used optimal interval,
- SM-0 – optimal interval calculated on the base of experiments leading to the algorithm SM-0
| Rep | Interval | Factor | SM-0 |
|---|---|---|---|
| 2 | 1.8 | 1 | |
| 3 | 7.8 | 4.36 | 7 |
| 4 | 16.8 | 2.15 | 16 |
| 5 | 30.4 | 1.80 | 35 |
| 6 | 50.4 | 1.66 | |
| 7 | 80.2 | 1.59 | |
| 8 | 124 | 1.55 | |
| 9 | 190 | 1.53 | |
| 10 | 288 | 1.52 | |
| 11 | 436 | 1.51 | |
| 12 | 654 | 1.50 | |
| 13 | 981 | 1.50 | |
| 14 | 1462 | 1.49 | |
| 15 | 2179 | 1.49 | |
| 16 | 3247 | 1.49 | |
| 17 | 4838 | 1.49 | |
| 18 | 7209 | 1.49 |
Obviously, the exact correspondence, to some extent, is a coincidence because the experiment leading to the formulation of the algorithm SM-0 was not that sensitive.
It is worth noticing, that optimal factors tend to decrease gradually! This fact seems to confirm recent observations based on the analysis of the matrix of optimal factors used in the algorithm SM-5.
If Laps o equals 4 ( forgetting index 10%, as in the algorithm SM-5) then the sequence of optimal factors resembles a column of the OF matrix in the algorithm SM-5. Also the knowledge retention matches almost ideally the one found in SM-5 databases.
| Rep | Interval | Retention | Factor |
|---|---|---|---|
| 2 | 3 | 93.21678 | |
| 3 | 16 | 93.80946 | 4.89 |
| 4 | 43 | 93.97184 | 2.74 |
| 5 | 102 | 94.04083 | 2.39 |
| 6 | 232 | 94.06886 | 2.27 |
| 7 | 517 | 94.08418 | 2.23 |
| 8 | 1138 | 94.09256 | 2.20 |
| 9 | 2502 | 94.09737 | 2.20 |
| 10 | 5481 | 94.09967 | 2.19 |
The value of retention was obtained by averaging its value calculated for each day of the optimal process:
R=(R(1)+R(2)+…+R(n))/n
R(d)=100-2.5*Laps(d-dlr)
where:
- R – average retention
- R(d) – retention on the d-th day of the process
- Laps(Int) – expected number of lapses after the interval I
- dlr – day of the process on which the last repetition was scheduled
Workload vs. Retention trade-off
Despite the inaccuracies coming from heterogeneous material, solid conclusion could be drawn about the impact of the forgetting index on the amount of time needed to invest in learning. Those observations survived the test of time:
Archive warning: Why use literal archives?
This text is part of: ” Optimization of learning ” by Piotr Wozniak (1990)
Very interesting conclusions may be drawn by comparison of retention and workload data calculated by means of the model of intermittent learning:
- Index – forgetting index (Laps o*2.5) determining optimal intervals in the process of time optimal learning scheduled with the use of the IL model
- Retention – overall retention obtained while using the given forgetting index (calculated upon elapse of 10,000 days)
- Repetitions – number of repetitions scheduled in the first 10,000 days of the process when using the given forgetting index,
- Factor – asymptotic value of the optimal factor (taken from the 10,000-th day of the process)
| Index | Retention | Repetitions | Factor |
|---|---|---|---|
| 2.5 | 97.76 | every 2 days | 1.0000 |
| 4.5 | 96.88 | 65 | 1.0300 |
| 5.0 | 96.64 | 30 | 1.1600 |
| 5.5 | 96.39 | 22 | 1.3000 |
| 6.25 | 96.01 | 17 | 1.4900 |
| 7.5 | 95.37 | 13 | 1.7700 |
| 10.0 | 94.10 | 10 | 2.1900 |
| 12.5 | 92.78 | 9 | 2.4700 |
Figure 11.2 demonstrates that the forgetting index used in determination of optimal intervals should fall into the range 5 to 10%.
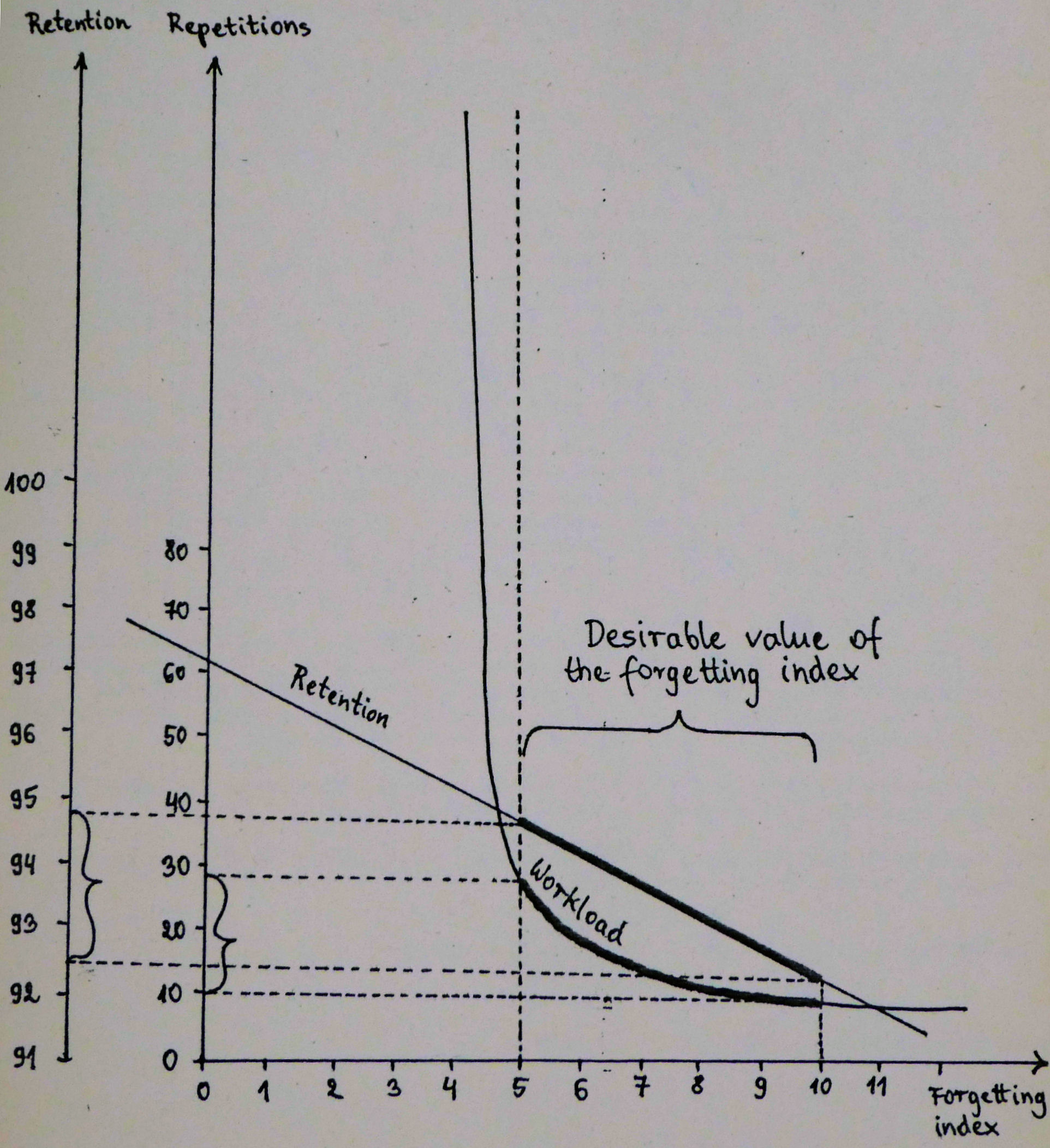
Fig. 11.2. Workload-retention trade-off: On one hand, if forgetting index is lower than 5%, then the workload increases dramatically without substantially affecting the retention. On the other, above forgetting index of 10%, workload hardly changes while retention steadily falls down. Obviously, the workload-retention trade-off corresponds directly to the compromise between the acquisition rate and retention. By increasing the availability of time X times (by decreasing the workload X times), one can increase the acquisition rate X times (compare Chapter 5). Note, that the relation of the forgetting index and retention in this model is almost linear. (source: Optimization of learning: Model of intermittent learning , Piotr Wozniak, 1990)
Another important observation comes from the calculation of the forgetting index for which the increase of strength is the greatest.
From the model of intermittent learning it follows that
S(n)=1.5*Laps(n)*S(n-1)*exp(-0.15*Laps(n))+1
Upon differentiation for the variable Laps(n) we arrive at:
S'(n)=1.5*S(n-1)*exp(-0.15*Laps(n))*(1-0.15*Laps(n))
Finally, after equating with zero, we obtain:
Laps(n)=7.8
which corresponds to the forgetting index equal to 20%! Such a forgetting index is equivalent to intervals 2 times longer than the optimal ones determined by the index equal 10% (as in the Algorithm SM-5). However, it must not be forgotten that it is the knowledge retention and not the strength of memory that is the only factor traded for workload. Therefore the above finding does not abolish the validity of the Algorithm SM-5.
Conclusions: model of intermittent learning
The ultimate conclusions drawn at the end of the chapter stood the test of 3 decades. Only the claim on non-exponential shape of forgetting curves is inaccurate. As the entire model was based on heterogeneous data, the exponential nature of forgetting could not have been revealed.
Archive warning: Why use literal archives?
This text is part of: ” Optimization of learning ” by Piotr Wozniak (1990)
Interim summary
- The model of intermittent learning was constructed making it possible to estimate knowledge retention upon different repetition schedules
- The model strongly indicates that the forgetting curve is not exponential [ wrong: see Exponential nature of forgetting]
- The model satisfactorily corresponds to experimental data
- With a striking accuracy, the model approximates optimal intervals and knowledge retention implied by the SuperMemo model
- The model indicates that optimal factors decrease in successive repetitions and asymptotically approach the ultimate value
- The model indicates that the desirable value of the forgetting index used in time optimal learning should fall into the range 5% to 10%
- The model indicates an almost linear relation of the forgetting index and knowledge retention
- The model shows that the greatest increase of the strength of memory occurs when intervals are approximately 2 times longer than that used in the SuperMemo method. This is equivalent to the forgetting index equal to 20%
1991: Employing forgetting curves
Painful birth of SuperMemo World (1991)
1991 was the most important year since the birth of SuperMemo. It was a year of big decisions, stress, drama, discovery and hard work. At the start of the year, there were three greatest believers in SuperMemo: Biedalak, Murakowski and myself. We were all in the same spot in our lives: transitioning from the years of unconcern in university to the uncertainty of independent adulthood. By default, we all dreamt of big science in the US: Biedalak dreamt of artificial intelligence, Murakowski of quantum physics, and I wanted to crack the secrets of molecular memory. In retrospect, graduate students from Eastern Bloc with good transcripts, exam results and rock-solid recommendations are pretty welcome in the US. Things get more complex if they demand full financial support. I did not have a penny. Moreover, eager Easterners were often treated as dutiful labor. Zeal for their own projects and great ideas might have been less welcome. I will never know. The three believers had all different visions for SuperMemo.
On Jan 3, 1991, I started the implementation of the new spaced repetition algorithm for SuperMemo 6. On the same day, Murakowski left for London where he would pursue his educational dreams while trying to sell SuperMemo 2. He would not sell via a distribution channel or in a shop. He would need to go from person to person, explain the merits of the program and hopefully collect a few bucks to keep the hope going.
In the meantime, Biedalak and I met regularly for a 10 km jogging that would be combined with winter swimming and a brainstorming session on the way back home. We mostly spoke of studying in the US and selling SuperMemo. More and more frequently, the idea of our own company started coming up.
I started my work over the new spaced repetition algorithm with some ideas that would change SuperMemo for ever. Algorithm SM-6 used in SuperMemo 6 was a breakthrough that would power further development over the next 25 years. It would re-employ the simple experimental procedure that led to spaced repetition in 1985 but would do it in an automated manner. It would collect performance data and choose the best time for review: it would plot the user’s forgetting curve. This would also mean that the user would be able to decide the acceptable probability of forgetting for every single item (i.e. the optimum level of retention-workload tradeoff).
At that time, I was still bound to 360 kB diskettes. For that reason, SuperMemo still could not keep all repetition histories that would fully replicate the 1985 approach on a massive scale. However, on Jan 6, 1990, I had a simple idea. I could just collect data about the forgetting curves for classes of items of different difficulty and stability. Instead of the full record, I would only update the approximation of how many items in a given class are retained in memory at a given time (i.e. at a given level of retrievability). That idea survives at the core of SuperMemo to this day. Even with the full record of repetition histories today, SuperMemo still instantly knows the expected retrievability of items in a given class.
At the crossroads in life, I was finally free from school. There is a powerful emotion that millions of teens and young adults face in their lives: a traumatic move from a slave called “pupil” or “student”, to the freedom of becoming an “unemployed adult”. The psychological shakeup can be even more dramatic if one turns from “good student” to “unemployed 28-year-old living with his mom”. Like a lightswitch: the whole world seems to change from cheerful support to a gloomy-faced condemnation mixed up with pity.
I kept learning and worked on new ideas for SuperMemo in the atmosphere of freedom mixed up with uncertainty. For me, uncertainty is an energizer. However, on Feb 12, 1991, I learned that my mom was diagnosed with terminal cancer. To the mix of freedom and uncertainty, it added the sense of gloom. For me again, gloom can also be an energizer. I tripled my learning about cancer as if in hope of finding out some magic therapy on my own. This shows how unreasonable optimism can be a key to productivity, and surviving hard times. By working harder I could dispel the gloom. High productivity is a sure anti-depressant. My hard work left no room for dark thoughts. I was confident, I would cure my mom!
Incidentally, at the moment of mom’s diagnosis, I was also writing a program to simulate the optimum behavior of memory in response to the environment; a way to prove what math would make the two component model of memory optimum. At the diagnosis, I threw that effort out of my schedule to learn about cancer. I never completed that program and that idea still lives in limbo pushed away by other projects.
On Mar 6, 1991, during one of our jogging-cum-brainstorming days with Biedalak, someone tossed the name SuperMemo World. Little did we know that four months later that would be the name of our company that has survived 27 years today.
On Mar 12, 1991, I made my first repetitions with the new algorithm in SuperMemo 6 while my mom rested on her deathbed. A week later, she died peacefully in sleep at the young age of 70. In similar circumstances, the usual picture involves family meetings, mourning, funeral, and a whole host of traditions with roots in religion that I could never accept as rational. Instead, 9 hours after my mom’s death, I worked on a better method for a fast approximation of the OF matrix. In that work, I capitalized on the job I once did for ZX Spectrum. I would employ linear regression along the difficulty columns and negative exponential regression along the repetition rows. Years later, I found that power regression is more appropriate for the latter. Only Algorithm SM-8 developed four years later would make a full use of those ideas. However, I mention it mostly to illustrate how hard work and productivity can work great as a remedy against gloom and possible depression. At that time I discovered that the impact of an emotional trauma follows a circadian curve. I would work hard in the morning, but the gloom would keep creeping back to my mind in the evening. Sleep would be the liberation and the best anti-depression. From those early days I am a firm believer in the idea that sleep and learning carry a solution to the problem of depression, however, I never truly had a chance to work on it. It would help if I suffered a bit myself, but either I have some good resilience endowment, or, more likely, I instinctively employ the tools of good sleep and high productivity at hard times. Ever since Sapolsky called depression the “worst disease in the world”, I wanted to find a formula for preventing depression. I sense there is a simple formula. Perhaps that naive childlike optimism itself is part of the solution?
On Apr 13, 1991, we decided that SuperMemo 2 should be released as freeware. We hoped it might educate potential users abroad about the power of spaced repetition. However, initially, we had to send out diskettes with free SuperMemo at our own cost. Only in 1993, we uploaded SuperMemo to a local BBS called “Onkonet”. It would take some more years before we could upload future versions to Simtel and freeware sites. That freeware idea had an interesting side effect: by the end of the year, it was clear: people would start using the program and then give up. This was a hint of an inherent problem with spaced repetition: poor motivation resulting from poor skills would produce a high drop out rate. We also heard that others would try to sell SuperMemo 2 as if this was a commercial product.
On May 2, 1991, I implemented the option for setting the requested forgetting index in SuperMemo 6. On July 5, 1991, SuperMemo World was born. One of the first investment was a PC with a hard disk that would finally help me move away from the slow era of floppy disks.
On Nov 23, 1991: SuperMemo was announced as the finalist of Software for Europe competition. This saved SuperMemo World.
Slow start of commercial SuperMemo
When we set up SuperMemo World with Krzysztof Biedalak on Jul 5, 1991, the future looked so bright we needed to buy shades. The earth is populated with the highly intelligent population that all need to learn things. This whole population is our market. The only problem was how to convince all those smart people that two poor students educated behind the Iron Curtain got anything of value to offer. We could not have used the web for that job. SuperMemo is older than the web itself. We could not afford advertising for lack of capital. There was no venture capital culture in Poland in 1991. All we could do is put the first few copies of SuperMemo in file folders and place them on shelves of nearby computer shops. As we aimed at global domination, we did not even have a manual in Polish. Instead of first sales, we had a long summer of silence and creeping doubts.

Figure: In 1991, we delivered the first copies of SuperMemo 5 for DOS to shops in Poznan (Poland) in pink folders with a sticker. The manual did not include a translation to Polish. Amazingly, we found a few buyers. The first sale took place some time between September 9 and 11, 1991 (computer shop Axe Prim)
(reconstructed on the basis of original folders and stickers)
Why was it hard to sell the first copy? I can reconstruct the scenario from the words of one of our first customers who actually visited a shop and had a look at the first SuperMemo displayed in public. On a shelf with computer programs, along with shiny boxes from Microsoft, he noticed a shabby folder with enticing words: ” Your breakthrough speed-learning software “. He picked up the folder and opened a manual, which was a stack of poorly xeroxed pages in English. With lofty words, he read a story that defied belief. It was all too good to be true. Faster learning, great retention, new scientific method, a little cost in time, etc. He did not contemplate an investment, the package was pretty costly (around $100, which was a lot in Poland 1991), however, he approached the salesperson to find out who the people behind SuperMemo were. The owner of the shop knew SuperMemo pretty well and explained. The story started looking credible. The customer never forgot the episode. A few months later, he heard of SuperMemo from some local journal and became one of the first paying customers. His registration coupon arrived in January 1992, and the history of his upgrades says he stayed with SuperMemo for decades and now his son is one of the regular customers.
However, back in summer 1991, we had no sales and by fall, everyone except for myself started having serious doubts. Not about SuperMemo, but about the viability of the business.
It should help to know how we have met. With Biedalak, we were friends since forever. I attended a school with his brother, we lived 200 meters apart and qualified for the same year of computer science in university. I cannot say how I convinced Biedalak that SuperMemo is great. We have just been too close and he has always been in the circle. This part was easy. Tomek Kuehn was one of the first great believers in SuperMemo. He was also a great programmer, a great inspiration, and he grasped the idea instantly. He wrote two versions of SuperMemo himself: for Atari 800 in 1988, and for Atari ST in 1989. In January 1989, he even sold 10 copies of SuperMemo 2 using an advert in one of the computer journals: Komputer. I presume, he did not recover the invested money. Upon graduation, he already had his own business: a computer shop. This shop was also one of the first to present SuperMemo to its customers. His partner and friend was Marczello Georgiew who did not need much convincing either. Last but not least, I met Janusz Murakowski during GRE exams in Budapest in 1990. A great mathematical mind, he might be the fastest convert to SuperMemo ever. During our train trip back to Poland, I mentioned SuperMemo. He was instantly captivated. A few days later, he was already an enthusiastic user of SuperMemo 2 (as of Jun 13, 1990). In our company rap anthem, we sang ” we are the guys who sell SuperMemo“. It was very hard to convince people that SuperMemo works, but the guys on the team have always been enthusiastic.
By November 1991, the enthusiasm was thawing. If we continued without success, we would have gradually lost the team in proportion to their involvement and passion. With a few more months, the company might have died. SuperMemo would not have died. I would certainly look for a buyer, or continue one way or another. I was too tied to the product. I used it myself and all my knowledge was invested in my databases. I might have thought of returning to the idea of a PhD in the US. In the same way as I was able to combine work at the university in Holland in 1989 with programming “after hours”, I would probably continue until some breakthrough, e.g. on the web. Perhaps it would be an open source product? Luckily, Dr Wojciech Makałowski of the Department of Biolpolymer Biochemistry suggested we submit SuperMemo for Software for Europe competition. By some miraculous stroke of good luck, we qualified for the final and this was instantly noticed by the Polish media, esp. computer journals. As of that point, SuperMemo had an easy ride with the Polish press that became more and more intrigued. Andrzej Horodeński was first, and Pawel Wimmer was second and most faithful to this very day. Wimmer actually used SuperMemo 2, which he probably received from Tomasz Kuehn at the time of his KOMPUTER journal advert in 1989.
1.5 years after its birth, SuperMemo World had finally become profitable. Not bad.
SuperMemo World was a fantastic set up from the getgo. We had no injection of venture capital in Poland in 1991, so we had to pull ourselves by our own bootstraps by selling, what others considered to be “snake oil”. We might have easily failed, but we survived by the sheer power of passion, belief, and a big stroke of good luck.
Origins of Algorithm SM-6
Algorithm SM-6 was first used in SuperMemo 6 (1991), however, it kept evolving in SuperMemo 7 (1992). There has never been the SM-7 version despite multiple changes. Most notably, as of 1994, the exponential function was used to approximate forgetting curves in SuperMemo 7 for Windows. OF matrix approximations have also been improved over time.
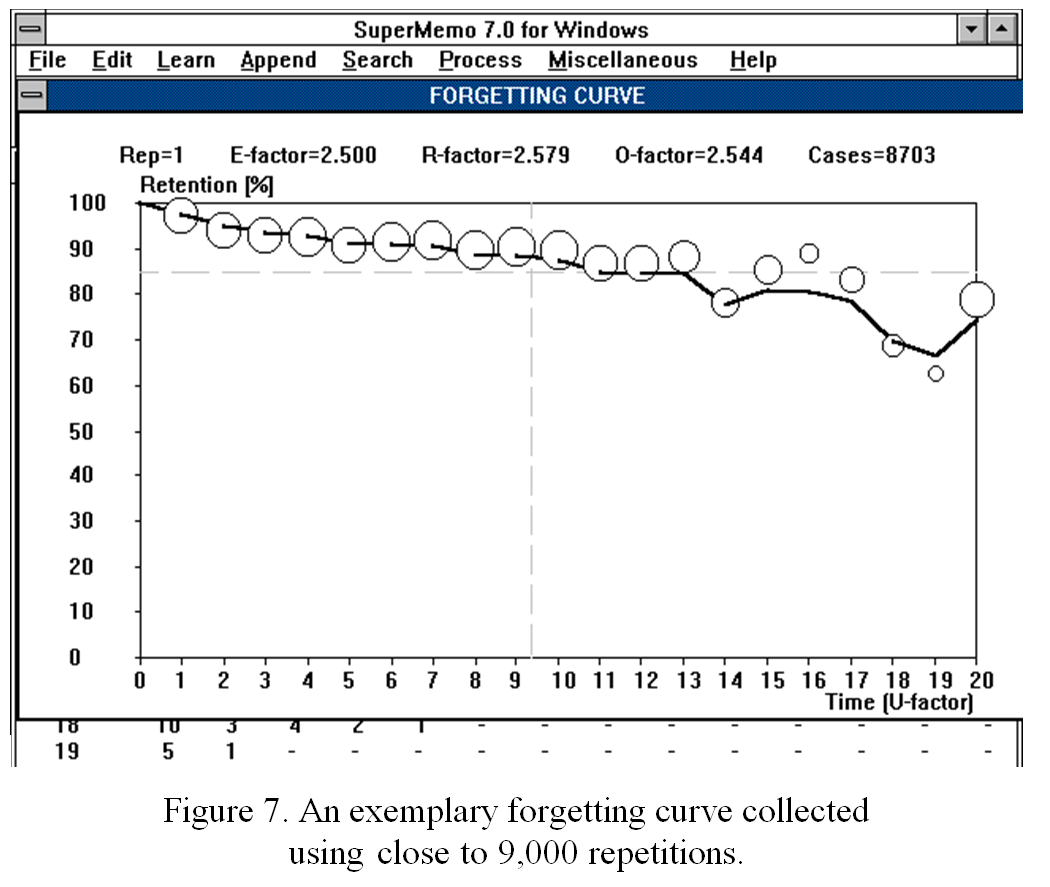
Figure: SuperMemo 7 for Windows (1992) displaying a forgetting curve based on averages.
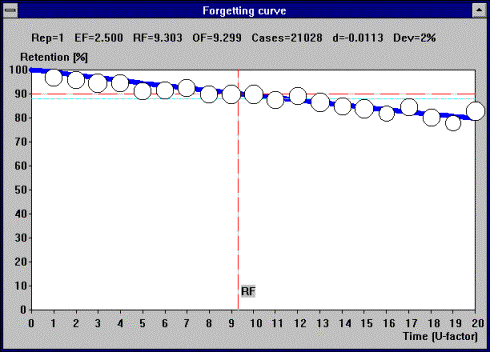
Figure: SuperMemo 7 for Windows (1994) displaying a forgetting curve approximated with an exponential function. Vertical axis represents recall in percent. Horizontal axis corresponds with time represented by U-Factor
The most important component of Algorithm SM-6 was to collect data on the rate of forgetting. Forgetting curves make it easy to accurately determine optimum intervals. This eliminated the need for a slow and inaccurate bang-bang approach of Algorithm SM-5:
Archive warning: Why use literal archives?
This text is part of: ” Economics of Learning ” by Piotr Wozniak (1995)
In Algorithm SM-5, the process of determining the value of a single entry of the matrix of optimal factors looked as follows (see before):
- Set the initial value to an average optimal factor value (OF) obtained in previous experiments
- If the grade produced by the entry in question was (1) greater than the desired value then increase the value of OF, (2) less than the desired value then decrease OF, or (3) equal the desired value then do not change OF
The above approach shows that the optimum value of OF could be reached only after a great number of repetitions, and what is worst, the greater the ordinal number of a repetition, the longer it would take to execute the modification-verification cycle (i.e. the cycle in which an OF entry is changed, and verified upon scheduling another repetition with a correspondingly long interval).
Introducing the concept of the forgetting index
The novelty of Algorithm SM-6 is to approximate the slope of the forgetting curve corresponding to a given entry of the matrix of optimal factors, and compute the new value of the relevant optimal factor directly from the approximated curve. In other words, no modification-verification cycle is necessary in Algorithm SM-6 because of establishing the deterministic relationship between the forgetting curve and the optimum inter-repetition interval. The modification of the optimal factor occurs immediately after a repetition upon approximating the new forgetting curve derived from data that include the grade provided in the recent response. This modification not only made it possible to greatly accelerate the process of determining the optimum values of the matrix of optimal factors, but also provided a means for establishing the desired level of knowledge retention that will be reached in the course of the learning process (see an exemplary forgetting curve).
The desired level of knowledge retention is determined by the proportion of items that are not remembered at repetitions. This proportion is called the forgetting index (items are classified as remembered or forgotten on the basis of grades provided by the student in self-assessment of his or her progress).
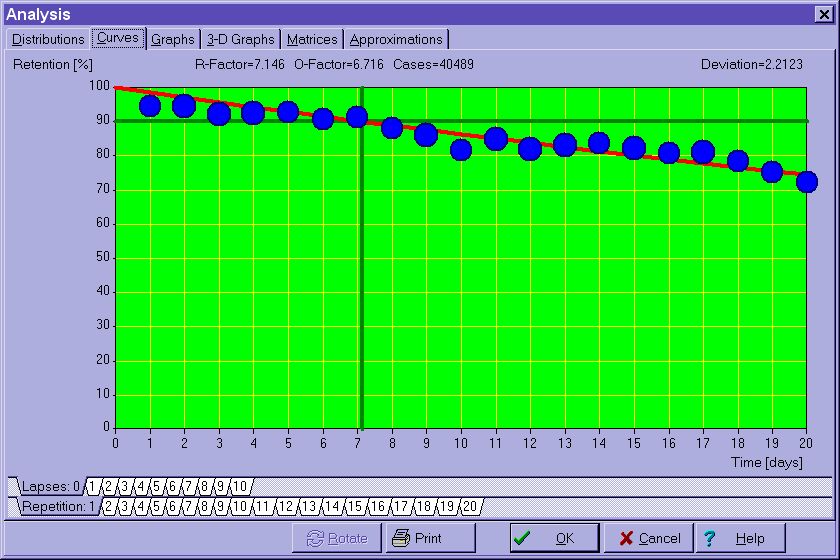
Figure: An exemplary forgetting curve plotted in the course of repetitions (over 40,000 repetition cases recorded).
In the figure presented above, the lapse of time is represented by the interval in days. The vertical axis represents knowledge retention stated as percentage. The horizontal line located at the retention level of 90% determines the requested forgetting index, i.e. the desired proportion of items that should be forgotten at the moment of repetition. The optimum interval will then naturally come at the cross-section of the requested forgetting index line with the forgetting curve. In the example above, the optimum interval equals seven days. The presented forgetting curve has been plotted on the basis of 40489 recorded repetition cases. See later in the text for explanation of the values R-Factor (RF), O-Factor (OF), etc.Because of the highly irregular nature of the matrix of optimal factors computed directly from forgetting curves, in Algorithm SM-6, the matrix used in spacing repetitions represents a smoothed version of the so-called matrix of retention factors (matrix RF), which is derived directly from forgetting curves corresponding to particular entries of the matrix OF. In other words, forgetting curves determine the value of entries of the matrix RF, and only the smoothed equivalent of the latter, the matrix OF is used in computing optimum intervals.
Algorithm SM-6
The description of the algorithm below is taken with some clarifications from my PhD Thesis, and refers to the status quo for 1994:
Archive warning: Why use literal archives?
This text is part of: ” Economics of Learning ” by Piotr Wozniak (1995)
- The learned knowledge is split into smallest possible pieces called items
- Items are formulated in the question-answer form
- Items are memorized by means of a self-paced drop-out technique, i.e., by responding to the asked questions as long as it takes to provide all correct answers
- After memorizing an item, the first repetition is scheduled after an interval that is the same for all of the items. Its value is determined by the desired level of knowledge retention, which in turn can be converted into an interval by using an average forgetting curve taken from an average database of an average student ( Wozniak 1994a). The desired retention is specified by means of the so-called forgetting index, which corresponds to the proportion of items forgotten at repetitions (to learn how to compute retention from the forgetting index, and vice versa). Note, that the first interval may be randomly shortened or lengthened for the sake of speeding up the optimization process (varying intervals increase the accuracy of approximating the forgetting curve).
- The first interval is computed as for an average student and an average database. However, as soon as the recorded value of the forgetting index deviates from the requested level, the length of the first interval is modified accordingly. The new value of the interval is derived from the approximation of the negatively exponential forgetting curve plotted in the course of repetition. With each repetition score recorded, the plot becomes more and more accurate and the used value of the optimum inter-repetition interval settles at the point that ensures the selected level of knowledge retention. After each repetition, the student produces a grade, which determines the accuracy and easiness of reproducing the correct answer.
- On the basis of the grades, items are classified into difficulty categories. Their difficulty is reestimated in each successive repetition. The difficulty of each item is characterized by the earlier mentioned E-factors (E stands for “easiness”). E-factors are equal to 2.5 for all items on the entry to the learning process, and modified after subsequent repetitions. For example, grades above four result in slightly increasing the E-factor (good grades indicate easy items), while grades below four reduce the E-factor. Historically, E-factors were used to determine how many times intervals should increase in successive repetitions of items of a given difficulty. At present, E-factors are only used to index the matrices of optimal factors and retention factors, and may bear little relevance to the actual interval increase.
- Different optimal intervals are applied to items of different difficulty.
- Different intervals are applied to items that have been repeated a different number of times.
- The function of optimal intervals is constantly modified in order to produce the desired knowledge retention determined by the forgetting index. In other words, the algorithm will detect how well the student copes with repetitions and adjust the length of inter-repetition intervals accordingly.
- The function of optimal intervals is represented as the matrix of optimal factors, OF-matrix in short, defined as follows:for n=1: I(n,EF)=OF(n,EF)for n>1: I(n,EF)=I(n-1,EF)*OF(n,EF)where:
- I(n,EF) – n-th interval for difficulty EF
- OF(n,EF) – optimal factor for the n-th repetition and the difficulty EF
- Matrix of optimal factors is produced by smoothing the so-called matrix of retention factors, RF matrix in short. Matrix of retention factors is defined in the same way as the matrix of optimal factors.
- Entries of the matrix of retention factors are intended to estimate the values of the entries of the matrix of optimal factors. Each optimal factor corresponds to an optimal interval that produces the desired retention at repetition (determined by the requested forgetting index). Each entry of the matrix of retention factors corresponds to a different value of E-factor and repetition number
- Entries of the matrix of retention factors, called R-factors , are computed from forgetting curves whose shape is sketched on the basis of the history of repetitions
- The lapse of time on the forgetting curve graph is measured by the so-called U-factor , which is the ratio of the current and the previous interval, except for the first repetition where U-factor equals the interval in days (as in Figure). The record of repetitions makes it possible to compute retention for different values of U-factor. The graph of the retention plotted versus the lapse of time (U-factor) represents a forgetting curve. The cross-section of the forgetting curve with the desired retention level determines the optimum R-factor, which, upon smoothing the matrix of retention factors, yields the optimum O-factor
- Each difficulty category and repetition number has its own record of repetitions used to sketch a separate forgetting curve. In other words, different intervals will be used for items of different difficulty, and for items repeated a different number of times.
- Intervals used in learning, including the first interval, are slightly dispersed round the optimal value in order to increase the accuracy of forgetting curve sketching, and consequently, to increase the convergence rate of the optimization procedure. By slightly dispersing intervals, the approximation of the forgetting curve will use a more scattered set of points on the graph
1994: Exponential nature of forgetting
Forgetting curve: power or exponential
The shape of the forgetting curve is vital for understanding memory. The math behind the curve may even weigh in on the understanding of the role of sleep (see later). When Ebbinghaus first determined the rate of forgetting, he got a pretty nice set of data with a good fit to the power function. However, today we know forgetting is exponential. The discrepancy is explained here.
Forgetting curve adapted from Hermann Ebbinghaus (1885). The curve has been rendered from original tabular data published by Ebbinghaus (Piotr Wozniak, 2017)
Wrong thinking helped spaced repetition
For many years, the actual shape of the curve did not play much of a role in spaced repetition. My early intuitions were all over the place depending on the context. Back in 1982, I was thinking that the evolution has designed forgetting for the brain to make sure we do not run out of memory space. The optimum time for forgetting would be determined by the statistical properties of the environment. Decay would be programmed to maximize survival. Once the review did not take place, the memory would get deleted to provide space for new learning.
I was wrong thinking that there might be an optimum time for forgetting and this error was actually helpful for inventing spaced repetition. That “optimum time” intuition helped the first experiment in 1985. The optimum time for forgetting would imply sigmoidal forgetting curve with a clear inflection point that determines optimality. Before the review, forgetting would be minimal. A delayed review would result in rapid forgetting. This is why finding the optimum interval seemed so critical. When data started pouring in later on, with my confirmation bias, I still could not see my error. I wrote in my Master’s Thesis about sigmoidal forgetting: ” this follows directly from the observation that before the elapse of the optimal interval, the number of memory lapses is negligible“. I must have forgotten my own forgetting curve plot produced in late 1984.
Today this seems preposterous, but even my model of intermittent learning provided some support for the theory. Exponential approximation yielded particularly high deviation error for data collected in my work on the model of intermittent learning, and the superposition of sigmoid curves for different E-Factors could easily mimic early linearity. Linear approximation seemed to excellently fit the model of intermittent learning within the recall range in the available data. No wonder, with whole pages of heterogeneous material, exponential nature of forgetting remained well hidden.
Contradictory models
I did not ponder forgetting curves much. However, my biological model dating back to 1988 spoke of exponential decay in retrievability. Apparently, in those days, the forgetting curve and retrievability could exist in my head as independent entities.
In my credit paper for a class in computer simulation (Dr Katulski, Jan 1988), my figures clearly show exponential forgetting curves:
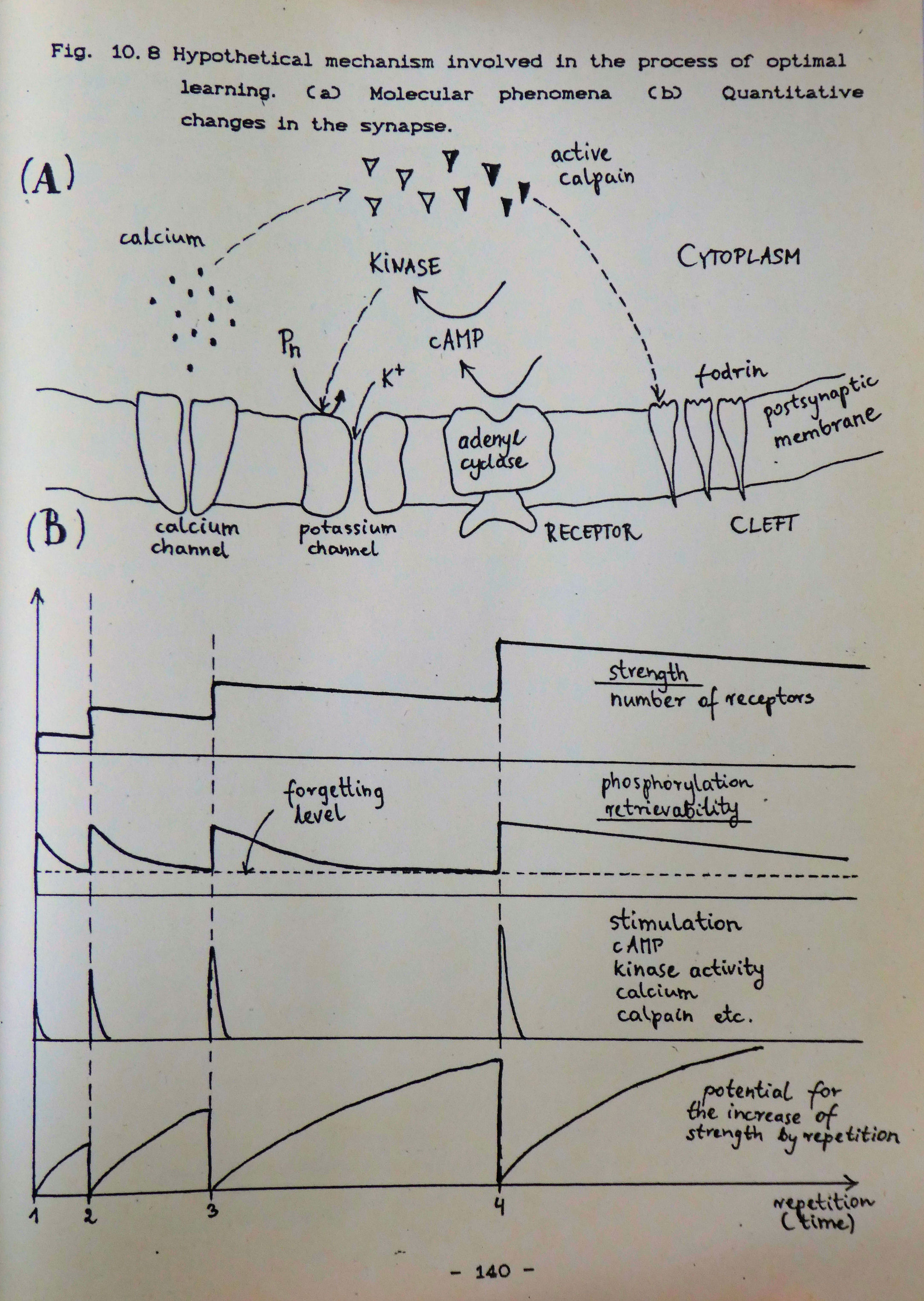
Figure: Hypothetical mechanism involved in the process of optimal learning. (A) Molecular phenomena (B) Quantitative changes in the synapse.
By that time I might have picked the better idea from literature. In the years 1986-1987, I spent a lot of time in the university library looking for some good research on spaced repetition. I found none. I might have already been familiar with Ebbinghaus’s forgetting curve. It is mentioned in my Master’s Thesis.
Collecting data
I collected data for my first forgetting curve plot in late 1984. As all the learning was done for learning’s sake over the course of 11 months, and the cost of the graph was minimal, I forgot about that graph and it lay unused for 34 years in my archives:
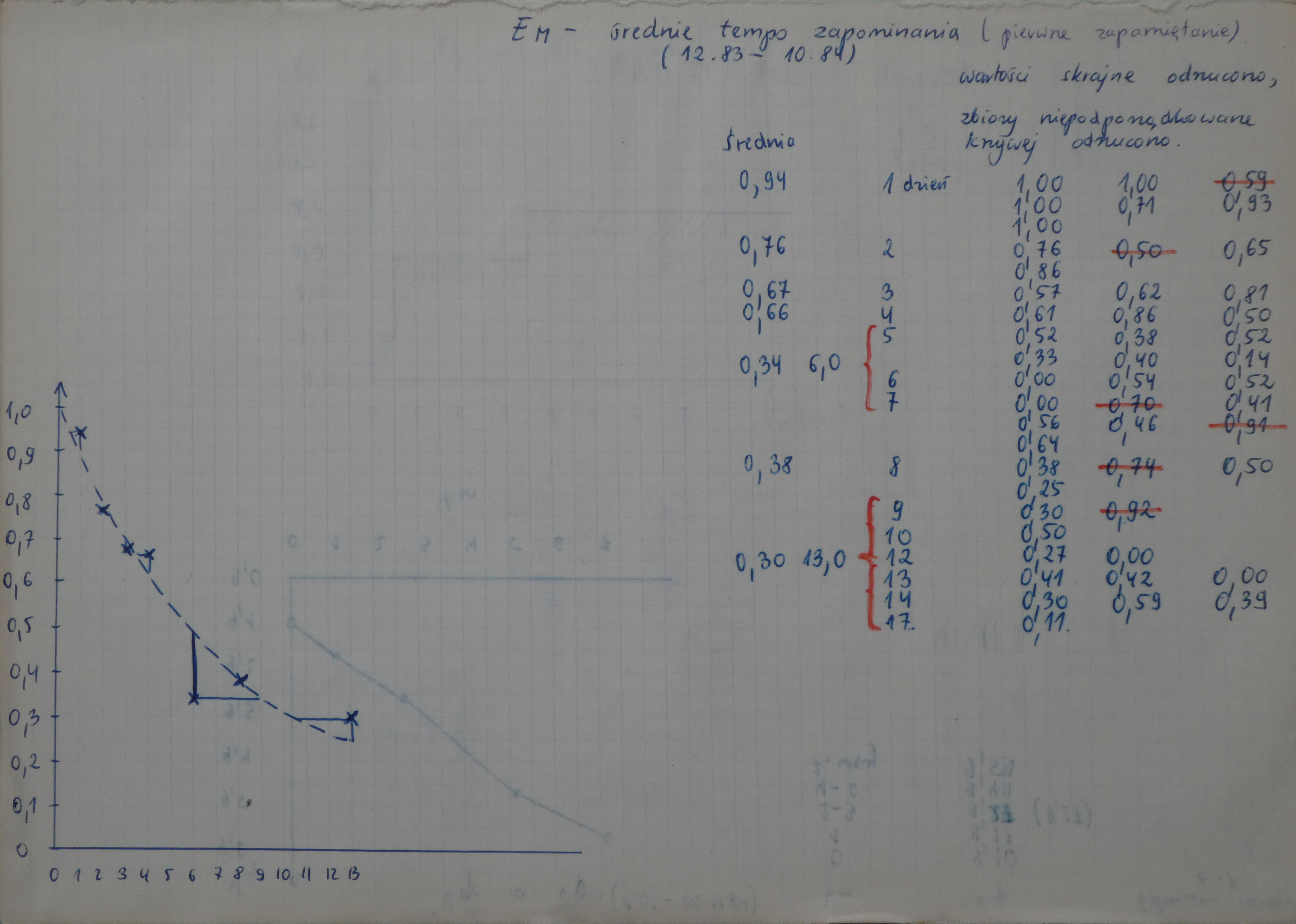
Figure: My very first forgetting curve for the retention of English vocabulary plotted back in 1984, i.e. a few months before designing SuperMemo on paper. This graph was not part of the experiment. It was simply a cumulative assessment of the results of intermittent learning of English vocabulary. The graph was soon forgotten. It was re-discovered 34 years later. After memorization, 49 pages of ~40 word pairs of English were reviewed at different intervals and the number of recall errors was recorded. After rejecting outliers and averaging, the curve appears to be far less steep that the curve obtained by Ebbinghaus (1885), in which he used nonsense syllables and a different measure of forgetting: saving on re-learning
My 1985 experiment could also be considered as a noisy attempt to collect forgetting curve data. However, first SuperMemos did not care about the forgetting curve. The optimization was bang-bang in nature, even though today, collecting retention data seems such an obvious solution (as in 1985).
Until I started collecting data with SuperMemo software, where each item could be scrutinized independently, I could not fully recover from early erroneous notions about forgetting.
SuperMemo 1 for DOS (1987) collected full repetition histories that would make it possible to determine the nature of forgetting. However, within 10 days (on Dec 23, 1987), I had to ditch the full record of repetitions. At that time, my disk space was 360KB. That’s correct. I would run SuperMemo from old type 5.25in diskettes. Full repetition history record returned to SuperMemo only 8 long years later (Feb 15, 1996) after the hectic effort from Dr Janusz Murakowski who considered every ticking minute a waste of valuable data that could power future algorithms and memory research. Two decades later, we have more data that we can effectively process.
Without repetition history, I could still investigate forgetting with a help of the forgetting curve data collected independently. On Jan 6, 1991, I figured out how to record forgetting curves in a small file that would not bloat the size of the database (i.e. without the full record of repetition history).
Only SuperMemo 6 then, in 1991, started collecting forgetting curve data to determine optimum intervals. It was doing the same thing as my first experiment, except it did it automatically, on a massive scale, and for memories separated into individual questions (this solved the heterogeneity problem). SuperMemo 6 initially used a binary chop to find the best moment corresponding with the forgetting index. A good fit approximation was still 3 years into the future.
First forgetting curve data
By May 1991, I had some first data to peek at, and this was a major disappointment. I predicted I would need a year to see any regularity. However, every couple of months, I kept noting down my disappointment with minimum progress. The progress in collecting data was agonizingly slow and the wait was excruciating. A year later, I was no closer to the goal. If Ebbinghaus was able to plot a good curve with nonsense syllables, his pain of non- coherence must have been worth it. With meaningful data, the truth was very slow to emerge. Even with the convenience of having it all done by a computer while having fun with learning.
On Sep 3, 1992, SuperMemo 7 for Windows made it possible to have a first nice peek at a real forgetting curve. The view was mesmerizing:
Figure: SuperMemo 7 for Windows was written in 1992. As of Sep 03, 1992, it was able to display user’s forgetting curve graph. The horizontal axis labeled U-Factor corresponded with days in this particular graph. The kinks between days 14 and 20 were one of the reasons it was difficult to determine the nature of forgetting. Old erroneous hypotheses were hard to falsify. Until the day 13, forgetting seemed nearly linear and might also provide a good exponential fit. It took two more years of data collecting to find answers (source: SuperMemo 7: User’s Guide)
Forgetting curve approximations
By 1994, I still was not sure about the nature of forgetting. I took data collected in the previous 3 years (1991-1994) and set out to figure out the curve once and for all. I focused on my own data from over 200,000 repetitions. However, it was not easy. If SuperMemo schedules a repetition at R=0.9, you can draw a straight line from R=1.0 to R=0.9 and do great with noisy data:
Figure: Difficulty approximating forgetting curve. Back in 1994, it was difficult to understand the nature of forgetting in SuperMemo because most of the data used to be collected in high recall range.
My notes from May 6, 1994 illustrate the degree of uncertainty:
Personal anecdote. Why use anecdotes?
May 6, 1994: All day of crazy attempts to better approximate forgetting curves. First I tried R=1-i n/(H n+i n) where i – interval, H – memory half-life, and n – cooperativity factor. Late in the evening, I had it work quite slowly, but … it appeared that r=exp(-a*i) works not much worse! Even the old linear approximation was not very much worse (sigmoid: D=8.6%, exponential D=8.8%, and linear D=10.8%). Perhaps, forgetting curves are indeed exponential? Going to sleep at 2:50
It was not easy to separate linear, power, exponential, Zipf, Hill, and other functions. Exponential, power and even linear approximations brought pretty good outcomes depending on circumstances that were hard to separate. Only when looking at forgetting curves well sorted for complexity at higher levels of stability, despite those graphs being data poor, could I see the exponential nature of forgetting more clearly.
One of the red herrings in 1994 was that, naturally, I had most data collected for the first review. New items at the entry to the process still provide a heterogeneous group that obeys the power law of forgetting.
The first review forgetting curve for newly learned knowledge collected with SuperMemo.
Later on, when they are sorted by complexity and stability, they start becoming exponential. In Algorithm SM-6, complexity and stability were imperfectly expressed by E-Factors and repetition number respectively. This resulted in algorithmic imperfections that made for imperfect sorting. In addition, SuperMemo stays within the area of high retention when forgetting is nearly linear.
By May 1994, the main first-review curve in my Advanced English database collected 18,000 data points and seemed like the best analytical material. However, that curve encompasses all the learning material that enters the process independent of its difficulty. Little did I know that this curve is covered by the power law. My best deviation was 2.0.
For a similar curve from 2018 see:
Figure: Forgetting curve obtained in 2018 with SuperMemo 17 for average difficulty (A-Factor=3.9). At 19,315 repetitions and least squares deviation of 2.319, it is pretty similar to the curve from 1994, except it is best approximated with an exponential function (for the power function example see: forgetting curve).
Exponential forgetting prevails
By summer 1994, I was reasonably sure of the exponential nature of forgetting. By 1995, we published “2 components of memory” with the formula R=exp(-t/S). Our publication remains largely ignored by mainstream science but is all over the web when forgetting curves are discussed.
Interestingly, in 1966, Nobel Prize winner Herbert Simon had a peek at Jost’s Law derived from Ebbinghaus work in 1897. Simon noticed that the exponential nature of forgetting necessitates the existence of a memory property that today we call memory stability. Simon wrote a short paper and moved on to hundreds of other projects he was busy with. His text was largely forgotten, however, it was prophetic. In 1988, similar reasoning led to the idea of the two component model of long-term memory.
Today we can add one more implication: If forgetting is exponential, it implies a constant probability of forgetting in unit time, which implies neural network interference, which implies that sleep might build stability not by strengthening memories, but by simply removing the cause of interference: unnecessary synapses. Giulio Tononi might then be right about the net loss of synapses in sleep. However, he believes that loss is homeostatic. Exponential forgetting indicates that this could be much more. It might be a form of ” intelligent forgetting” of things that interfere with key memories reinforced in waking.
Negatively exponential forgetting curve
Only in 2005, we wrote more extensively about the exponential nature of forgetting. In a paper presented by Dr Gorzelańczyk in a modelling conference in Poland, we wrote:
Archive warning: Why use literal archives?
Although it has always been suspected that forgetting is exponential in nature, proving this fact has never been simple. Exponential decay appears standardly in biological and physical systems from radioactive decay to drying wood. It occurs anywhere where expected decay rate is proportional to the size of the sample, and where the probability of a single particle decay is constant. The following problems have hampered the effort of modeling forgetting since the years of Ebbinghaus (Ebbinghaus, 1885):
- small sample size
- sample heterogeneity
- confusion between forgetting curves, re-learning curves, practise curves, savings curves, trials to learn curves, error curves, and others in the family of learning curves
By employing SuperMemo, we can overcome all these obstacles to study the nature of memory decay. As a popular commercial application, SuperMemo provides virtually unlimited access to huge bodies of data collected from students all over the world. The forgetting curve graphs available to every user of the program ( Tools : Statistics : Analysis : Forgetting curves) are plotted on relatively homogenous data samples and are a bona fide reflection of memory decay in time (as opposed to other forms of learning curves). The quest for heterogeneity significantly affects the sample size though. It is important to note that the forgetting curves for material with different memory stability and different knowledge difficulty differ. Whereas memory stability affects the decay rate, heterogeneous learning material produces a superposition of individual forgetting curves, each characterized by a different decay rate. Consequently, even in bodies with hundreds of thousands of individual pieces of information participating in the learning process, only relatively small homogeneous samples of data can be filtered out. These samples rarely exceed several thousands of repetition cases. Even then, these bodies of data go far beyond sample quality available to researchers studying the properties of memory in controlled conditions. Yet the stochastic nature of forgetting still makes it hard to make an ultimate stand on the mathematical nature of the decay function (see two examples below). Having analyzed several hundred thousand samples we have come closest yet to show that the forgetting is a form of exponential decay.
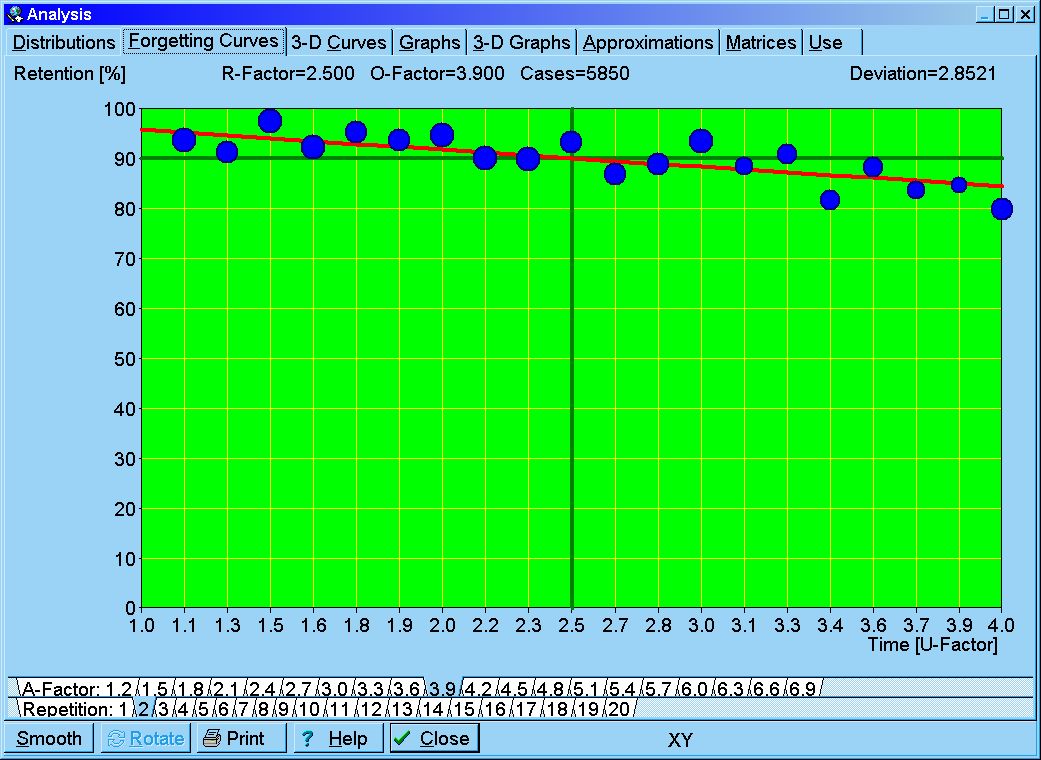
Figure: Exemplary forgetting curve sketched by SuperMemo. The database sample of nearly a million repetition cases has been sifted for average difficulty and low stability (A-Factor=3.9, S in [4,20]), resulting in 5850 repetition cases (less than 1% of the entire sample). The red line is a result of regression analysis with R=e -kt/S. Curve fitting with other elementary functions demonstrates that the exponential decay provides the best match to the data. The measure of time used in the graph is the so-called U-Factor defined as the quotient of the present and the previous inter-repetition interval. Note that the exponential decay in the range of R from 1 to 0.9 can plausibly be approximated with a straight line, which would not be the case had the decay been characterized by a power function.
Figure: Exemplary forgetting curve sketched by SuperMemo. The database sample of nearly a million repetition cases has been sifted for average difficulty and medium stability (A-Factor=3.3, S > 1 year) resulting in 1082 repetition cases. The red line is a result of regression analysis with R=e -kt/S.
Forgetting curve: Retrievability formula
In Algorithm SM-17, retrievability R corresponds with the probability of recall and represents the exponential forgetting curve. Retrievability is derived from stability and the interval:
R[n]:=exp -k*t/S[n-1]
where:
- R[n] – retrievability at the n-th repetition
- k – decay constant
- t – time ( interval)
- S[n-1] – stability after the (n-1)th repetition
That neat theoretical approach is made a bit more complex when we consider that forgetting may not be perfectly exponential if items are difficult or with mixed difficulty. In addition, forgetting curves in SuperMemo can be marred by user strategies.
In Algorithm SM-8, we hoped that retrievability information might be derived from grades. This turned out to be false. There is very little correlation between grades and retrievability, and it primarily comes from the fact that complex items get worse grades and tend to be forgotten faster (at least at the beginning).
Retention vs. the forgetting index
Exponential nature of forgetting implies that the relationship between the measured forgetting index and knowledge retention can accurately be expressed using the following formula:
Retention = -FI/ln(1-FI)
where:
- Retention – overall knowledge retention expressed as a fraction (0..1),
- FI – forgetting index expressed as a fraction (forgetting index equals 1 minus knowledge retention at repetitions).
For example, by default, well-executed spaced repetition should result in retention 0.949 (i.e. 94.9%) for the forgetting index of 0.1 (i.e. 10%). 94.9% illustrates how much exponential decay resembles a linear function at first. For linear forgetting, the figure would be 95.000% (i.e. 100% minus half the forgetting index).
Forgetting curve for poorly formulated material
In 1994, I was lucky my databases were largely well-formulated. This often wasn’t the case with users of SuperMemo. For badly-formulated items, the forgetting curve is flattened. It is not purely exponential (as superposition of several exponential curves). SuperMemo can never predict the moment of forgetting of a single item. Forgetting is a stochastic process and can only operate on averages. A frequently propagated fallacy about SuperMemo is that it predicts the exact moment of forgetting: this is not true, and this is not possible. What SuperMemo does is a search for intervals at which items of given difficulty are likely to show a given probability of forgetting (e.g. 10%). Those flattened forgetting curves led to a paradox. Neglecting complex items may lead to a great survival after long breaks from review. Even for a pure negatively exponential forgetting curve, a 10-fold deviation in interval estimation will result in R2=exp 10*ln(R1) difference in retention. This is equivalent to a drop from 98% to 81%. For a flattened forgetting curve typical of badly-formulated items, this drop may be as little as 98%->95%. This leads to a conclusion that keeping complex material at lower priorities is a good learning strategy.
Power law emerges in superposition of exponential forgetting curves
To illustrate the importance of homogenous samples in studying forgetting curves, let us see the effect of mixing difficult knowledge with easy knowledge on the shape of the forgetting curve. The figure below shows why heterogeneous samples may lead to wrong conclusions about the nature of forgetting. The heterogeneous sample in this demonstration is best approximated with a power function! The fact that power curves emerge through averaging of exponential forgetting curves has earlier been reported by others (Anderson&Tweney 1997; Ritter&Schooler, 2002).
Figure: Superposition of forgetting curves may result in obscuring the exponential nature of forgetting. A theoretical sample of two types of memory traces has been composed: 50% of the traces in the sample with stability S=1 (thin yellow line) and 50% of the traces in the sample with stability S=40 (thin violet line). The superimposed forgetting curve will, naturally, exhibit retrievability R=0.5*Ra+0.5*Rb=0.5*(e -k*t+e -k*t/40). The forgetting curve of such a composite sample is shown in granular black in the graph. The thick blue line shows the exponential approximation (R2=0.895), and the thick red line shows the power approximation of the same curve (R2=0.974). In this case, it is the power function that provides the best match to data, even though the forgetting of sample subsets is negatively exponential.
SuperMemo 17 also includes a single forgetting curve that is best approximated by a power function. This is the first forgetting curve after memorizing items. At the time of memorization, we do not know item complexity. This is why the material is heterogeneous and we get a power curve of forgetting.
Figure: The first review forgetting curve for newly learned knowledge collected with SuperMemo. Power approximation is used in this case due to the heterogeneity of the learning material freshly introduced in the learning process. Lack of separation by memory complexity results in superposition of exponential forgetting with different decay constants. On a semi-log graph, the power regression curve is logarithmic (in yellow), and appearing almost straight. The curve shows that in the presented case recall drops merely to 58% in four years, which can be explained by a high reuse of memorized knowledge in real life. The first optimum interval for review at retrievability of 90% is 3.96 days. The forgetting curve can be described with the formula R=0.9907*power(interval,-0.07), where 0.9907 is the recall after one day, while -0.07 is the decay constant. In this is case, the formula yields 90% recall after 4 days. 80,399 repetition cases were used to plot the presented graph. Steeper drop in recall will occur if the material contains a higher proportion of difficult knowledge (esp. poorly formulated knowledge), or in new students with lesser mnemonic skills. Curve irregularity at intervals 15-20 comes from a smaller sample of repetitions (later interval categories on a log scale encompass a wider range of intervals)
1995: Hypermedia SuperMemo
Birth of Algorithm SM-8 in a mountain hut
In 1995, SuperMemo was rewritten from grounds up and it was a great opportunity to implement a new spaced repetition algorithm based on data collected in 4 years of the use of Algorithm SM-6.
In March 1995 at CeBIT in Hannover, we saw a new fantastic development environment from Borland: Delphi. It has lifted the old Borland Pascal to a new level and opened dozens of development opportunities for SuperMemo. We decided to redesign the program along the lines depicted in my PhD dissertation. In addition to spaced repetition, we wanted to have knowledge structure and hypermedia. Instead of a mass of items, the users would build a knowledge tree. Instead of the old template of a question, answer, picture, and sound, we wanted to have all possible component types that could be mixed up into new hypermedia forms for expressing knowledge. There was also a dream of programmable SuperMemo in which developers could write their own procedures for any form of training, incl. procedural training, touch typing, or solving quadratic equations. At the same time, we have collected a lot of data that indicated that the algorithm used in SuperMemo could be improved. For example, the mathematical nature of the matrix of optimal factors has become pretty obvious.
In May 1995, I took my Pentium PC to a remote mountain hut in southern Poland to work on those ideas. That was a period of 100 days of total isolation interrupted only by a short visit from Krzysztof Biedalak during which we re-synchronized our vision for future SuperMemo. By September 1995, the new algorithm was ready and tested on my own data. Back in Poznan, I started gradually moving all my learning process from multiple collections in SuperMemo 7 to the new environment nicknamed “Genius”. Genius became SuperMemo 8 only two years later when the new program added up all functionality that was originally available in SuperMemo 7.
The main data that helped develop Algorithm SM-8 were forgetting curves and OF matrix data collected with SuperMemo 6 and SuperMemo 7. This data took away a great deal of guesswork from the algorithm. The work was pretty easy in comparison to Algorithm SM-17 (2014-2016) when I had mountains of repetition histories to process, and the requirements for precision and good metrics have tripled. While Algorithm SM-17 took two years to develop, Algorithm SM-8 was designed, implemented, and well-tested in mere 100 days.
The main ideas behind Algorithm SM-8:
- precise mathematical determination of the OF matrix based on live approximations. Instead of matrix smoothing known from SuperMemo 5, I wanted to know the exact mathematical function that could describe the matrix and perform live updates. It was easy to determine that a negative power function would determine OF=f(RepNo) (which is an expression of SInc=f(S)) in today’s terms). A bit more guesswork went into the impact of difficulty on SInc. I opted for a linear approximation of the function mapping difficulty ( A-Factor) to the decay constant for SInc (D-Factor), which expressed the decline in stability increase with stability/interval. That linear bet has survived to this day. It was a good guess.
- with a good definition of the OF matrix, I could provide a precise definition of item difficulty: instead of a fluid E-Factor that could be manually controlled by grades at the whim of the user, I wanted to have an absolute difficulty A-factor, which was defined as the stability increase after the first repetition timed for R=0.9. This made it possible for SuperMemo to adjust item difficulty with each repetition by correcting the fit of item’s performance with the expected performance based on the OF matrix
- faster determination of startup difficulty by correlating the first grade with the A-factor. This is a weak mechanism of little significance, as shown by the fact that even with multi-repetition histories, item difficulty is still a hazy concept. In that context, users should be reminded that the best approach is to formulate items well and just keep them easy
- approximating the first post-lapse interval by an exponential fit based on the number of memory lapses. The biggest value of that approach was to abolish a myth that reducing the length of intervals in case of memory lapses could speed up learning (some authors of software based on Algorithm SM-2 opted for such a solution, which has been proven wrong)
- the idea to correlate grades with the forgetting index was a failure and did not contribute to improving the algorithm. That truth transpired slowly. It took nearly a decade to come to the ultimate verdict: grades correlate poorly with the forgetting index. The intuition born with Algorithm SM-2 is only weakly correct
Interestingly, Algorithm SM-8 did not require full repetition history for elements. Full repetition histories were to be implemented only in Feb 1996. The advantage was an easier implementation. The disadvantage came with the fact that once the user intervened manually in the learning process, the algorithm had no record of that intervention, and could not defend itself from a possible inflow of incorrect data. Naturally, only full repetition history record made it possible to implement Algorithm SM-17 two decades later.
My first “live” repetition in Algorithm SM-8 on my own data took place on Aug 16, 1995, Wed. For the test, I “sacrificed” a small 100 item collection with mnemonic peg list for memorizing numbers. Over the next two years, I gradually converted all my other collections to work with the new algorithm and in the new SuperMemo environment. In 1997, all my knowledge have finally been integrated into a single well-structured database. In 1995-1997, we called such a database a “knowledge system”. Today we just call it collection (as in a collection of pieces of knowledge).
To this day, the core of the algorithm born in 1995 runs in SuperMemo 17 in the background, and the user can still choose intervals based on that old algorithm in case he is unhappy with propositions of Algorithm SM-17.
Absolute item difficulty
In SuperMemo 1.0 through SuperMemo 3.0, E-Factors were defined in the same way as O-Factors (i.e. the ratio of successive intervals). They were an approximate measure of item difficulty (the higher the E-Factor, the easier the item). However, the spaced repetition optimization would force E-factors to correspond with stability increase which drops with stability. In other words, by definition, in Algorithm SM-2, items would be tagged as more and more “difficult” as they were subject to successive repetitions. This is a bit counter-intuitive and users never seemed to notice.
Starting with SuperMemo 4.0, E-Factors were used to index the matrix of O-Factors. They were still used to reflect item difficulty. They were still used to compute O-Factors. However, they could differ from O-Factors and thus make for a better reflection of difficulty.
In SuperMemo 4 through SuperMemo 7, difficulty of material in a given database would shape the relationship between O-Factors and E-Factors. For example, in an easy collection, the starting-point O-Factor (i.e. the one corresponding with the first repetition and the assumed starting difficulty) would be relatively high. As performance in repetitions determines E-Factors, items of the same difficulty in an easy collection would naturally have a lower E-Factor than the exactly same items in a difficult collection. This all changed in SuperMemo 8 where A-Factors where introduced. A-Factors are “bound” to the second row of the O-Factor matrix. This makes them an absolute measure of item difficulty. Their value does not depend on the content of the collection . For example, you know that if A-Factor is 1.5, the third repetition will take place in an interval that is 50% longer than the first interval.
Archive warning: Why use literal archives?
A-Factor is a number associated with every element in a collection. A-Factor determines how much intervals increase in the learning process. The higher the A-Factor, the faster the intervals increase. A-Factors reflect item difficulty. The higher the A-Factor the easier the item. The most difficult items have A-Factors equal to 1.2. A-Factor is defined as the quotient of the second optimum interval and the first optimum interval used in repetitions
Post-lapse interval
Post-lapse interval approximation in Algorithm SM-8 abolished two myths:
- shortening intervals after a lapse is a good idea (this idea was advocated multiple times in the years 1991-2000)
- the first interval should always be 1 day (as in some older SuperMemo solutions)
In the graph presented below, we can see that with successive lapses, the optimum post-lapse interval keeps getting slightly shorter. This expresses nothing else but the fact that those high-lapse counts are reached only by badly formulated items, or items that are really hard to remember for their semantic nature or knowledge interference. For memories starting with Lapse=10, I suggested a term ” toxic” to express their impact on the learning process. If the brain rejected a piece of information that many times, we should get a message: this knowledge is badly formulated or has become toxic for other reasons (e.g. stress associated with learning, e.g at school).
Archive warning: Why use literal archives?
First interval – the length of the first interval after the first repetition depends on the number of times a given item has been forgotten. Note that the first repetition here means the first repetition after forgetting, not the first repetition ever. In other words, a twice-repeated item will have the repetition number equal to one after it has been forgotten; the repetition number will not equal three. The first interval graph shows exponential regression curve that approximates the length of the first interval for different numbers of memory lapses (including the zero-lapses category that corresponds with newly memorized items). In the graph below, blue circles correspond to data collected in the learning process (the greater the circle, the more repetitions have been recorded).
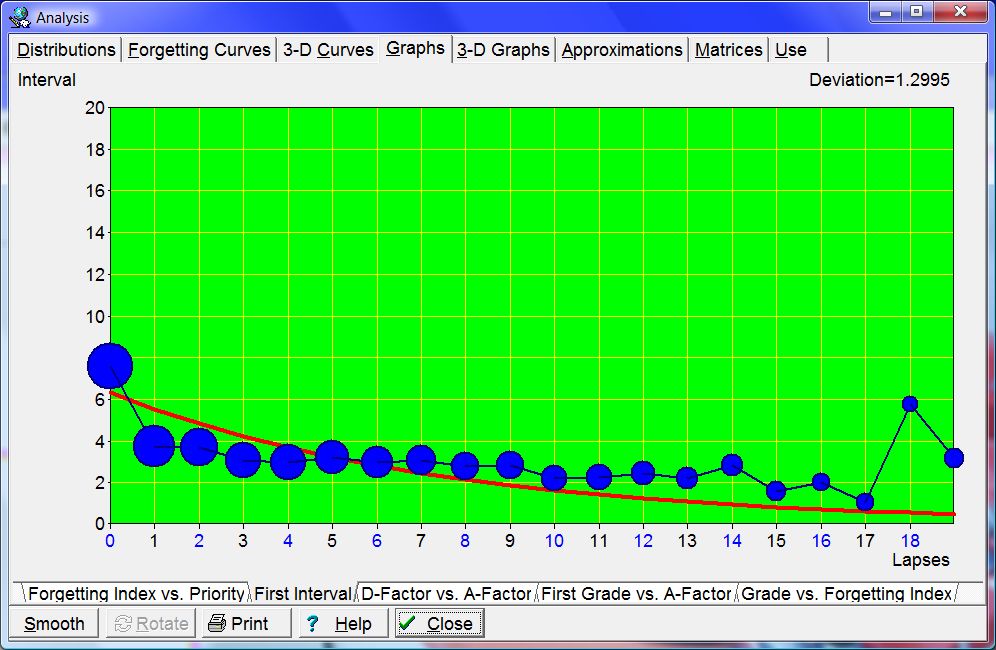
Figure: In the graph above, which includes data from over 130,000 repetitions, newly memorized items are optimally repeated after seven days. However, the items that have been forgotten 10 times (which is rare in SuperMemo) will require an interval of two days. (Due to logarithmic scaling, the size of the circle is not linearly proportional to the data sample; the number of repetition cases for Lapses=0 is by far larger than for Lapses=10, as can be seen in Distributions : Lapses)
First grade vs. A-Factor
Correlating the first grade with the estimated item difficulty was to help classify items by difficulty at the entry to the learning process. The correlation appears to be weak and is highly dependent on user’s grading system. For some users, there is virtually no correlation (picture #1). For others, the correlation is good enough to cover the full range of difficulty (A-factor) (picture #2).
In addition, in Algorithm SM-11 derived from Algorithm SM-8, the user was allowed to execute premature repetitions. Those repetitions would account for the spacing effect, however, they would still contribute to the graph and overestimate the grade for difficult items. With extensive use of incremental reading, this would flatten the graph.
Algorithm SM-17 does not use grade-difficulty correlation and derives difficulty from the entire repetition history. Practice shows that even then the estimate is hard to make and the good practice of learning is to keep all items easy (i.e. in the accepted mnemonic fit with the rest of the student’s knowledge).
Archive warning: Why use literal archives?
First Grade vs. A-Factor – G-AF graph correlates the first grade obtained by an item with the ultimate estimation of its A-Factor value. At each repetition, the current element’s old A-Factor estimation is removed from the graph and the new estimation is added. This graph is used by Algorithm SM-15 to quickly estimate the first value of A-Factor at the moment when all we know about an element is the first grade it has scored in its first repetition.
Grade vs. Forgetting Index
By correlating grades with the expected forgetting index (predicted retrievability), I hoped to be able to compute the estimated forgetting index (post-repetition estimate of the actual retrievability). This correlation appeared to be weak due to the fact that all users tend to deploy their own grading systems, which is often inconsistent. The grade and R correlation comes primarily from the fact that complex items get worse grades and tend to be forgotten faster (at least at the beginning). In that sense, grades provide a better reflection of complexity than a reflection of retrievability.
In the picture below, the entire range of the expected forgetting index seems to fall around the grade 3.
For Grade<=3 we can read the maximum estimated forgetting index, and for Grade>=4 we can read the minimum estimated forgetting index. In that light, two grade systems would have the exact same effect on the algorithm as the six grade system.
For other users, the curve might even peak at some levels of the expected forgetting index as if grading reflected a wish to remember items that are really hard to remember (lenient grading).
Algorithm SM-17 makes an extensive use of retrievability estimated after the repetition, however, it derives it from sheer recall data and the expected retrievability. Grade-retrievability correlations are also collected, however, their weight is negligible.
Archive warning: Why use literal archives?
Grade vs. Forgetting Index – FI-G graph correlates the expected forgetting index with the grade scored at repetitions. You need to understand Algorithm SM-15 to understand this graph. You can imagine that the forgetting curve graph might use the average grade instead of the retention on its vertical axis. If you correlated this grade with the forgetting index, you would arrive at the FI-G graph. This graph is used to compute an estimated forgetting index that is, in turn, used to normalize grades (for delayed or advanced repetitions) and estimate the new value of item’s A-Factor. The grade is computed using the formula: Grade=exp A*FI+B , where A and B are parameters of an exponential regression run over raw data collected during repetitions.
The FI-G graph is updated after each repetition by using the expected forgetting index and actual grade scores. The expected forgetting index can easily be derived from the interval used between repetitions and the optimum interval computed from the OF matrix. The higher the value of the expected forgetting index, the lower the grade. From the grade and the FI-G graph, we can compute the estimated forgetting index which corresponds to the post-repetition estimation of the forgetting probability of the just-repeated item at the hypothetical pre-repetition stage. Because of the stochastic nature of forgetting and recall, the same item might or might not be recalled depending on the current overall cognitive status of the brain; even if the strength and retrievability of memories of all contributing synapses is/was identical! This way we can speak about the pre-repetition recall probability of an item that has just been recalled (or not). This probability is expressed by the estimated forgetting index.
Algorithm SM-15
Algorithm SM-8 has been improved over years and evolved into Algorithm SM-11 (2002) and then Algorithm SM-15 (2011). Here I only present the latest version: Algorithm SM-15 (used in SuperMemo 15, SuperMemo 16, and as backup in SuperMemo 17).
The key improvements added to Algorithm SM-8 over two decades were:
- improved stability indexing: instead of using repetition numbers, as of SuperMemo 8 (1997), the algorithm used the concept of “repetition category” which roughly translates to stability
- tolerance for advanced and delayed repetitions, as of SuperMemo 11 (2002): a heuristic has been added to account for the spacing effect
- extending the representation of time in U-Factors from 60 days to 15 years (2011)
- correcting forgetting curve data for repetition delay beyond the original U-Factor span (2011)
Archive warning: Why use literal archives?
Algorithm SM-15 begins the effort to compute the optimum inter-repetition intervals by storing the recall record of individual items (i.e. grades scored in learning). This record is used to estimate the current strength of a given memory trace, and the difficulty of the underlying piece of knowledge (item). The item difficulty expresses the complexity of memories, and reflects the effort needed to produce unambiguous and stable memory traces. SuperMemo takes the requested recall rate as the optimization criterion (e.g. 95%), and computes the intervals that satisfy this criterion. The function of optimum intervals is represented in a matrix form (OF matrix) and is subject to modification based on the results of the learning process. Although satisfying the optimization criterion is relatively easy, the complexity of the algorithm derives from the need to obtain maximum speed of convergence possible in the light of the known memory models.
Important! Algorithm SM-15 is used only to compute the intervals between repetitions of items. Topics are reviewed at intervals computed with an entirely different algorithm (not described here). The timing of topic review is optimized with the view to managing the reading sequence and is not aimed at aiding memory. Long-term memories are formed in SuperMemo primarily with the help of items, which are reviewed along the schedule computed by Algorithm SM-15.
This is a more detailed description of the Algorithm SM-15:
- Optimum interval: Inter-repetition intervals are computed using the following formula:I(1)=OF[1,L+1]I(n)=I(n-1)*OF[n,AF]where:
- OF – matrix of optimal factors, which is modified in the course of repetitions
- OF[1,L+1] – value of the OF matrix entry taken from the first row and the L+1 column
- OF[n,AF] – value of the OF matrix entry that corresponds with the n-th repetition, and with item difficulty AF
- L – number of times a given item has been forgotten (from ” memory Lapses“)
- AF – number that reflects absolute difficulty of a given item (from ” Absolute difficulty Factor“)
- I(n) – n-th inter-repetition interval for a given item
- Advanced repetitions: Because of possible advancement in executing repetitions (e.g. forced review before an exam), the actual optimum factor (OF) used to compute the optimum interval is decremented by dOF using formulas that account for the spacing effect in learning:dOF=dOF max* a/(t half+ a)dOF max=(OF-1)*(OI+t half-1)/(OI-1)where:
- dOF – decrement to OF resulting from the spacing effect
- a – advancement of the repetition in days as compared with the optimum schedule (note that there is no change to OF if a=0, i.e. the repetition takes time at optimum time)
- dOF max – asymptotic limit on dOF for infinite a (note that for a=OI-1 the decrement will be OF-1 which corresponds to no increase in inter-repetition interval)
- t half – advancement at which there is half the expected increase to synaptic stability as a result of a repetition (presently this value corresponds roughly to 60% of the length of the optimum interval for well-structured material)
- OF – optimum factor (i.e. OF[n,AF] for the n-th interval and a given value of AF)
- OI – optimum interval (as derived from the OF matrix)
- Delayed repetitions: Because of possible delays in executing repetitions, the OF matrix is not actually indexed with repetitions but with repetition categories. For example if the 5-th repetition is delayed, OF matrix is used to compute the repetition category, i.e. the theoretical value of the repetition number that corresponds with the interval used before the repetition. The repetition category may, for example, assume the value 5.3 and we will arrive at I(5)=I(4)*OF[5.3,AF] where OF[5.3,AF] has a intermediate value derived from OF[5,AF] and OF[6,AF]
- Matrix of optimum intervals: SuperMemo does not store the matrix of optimum intervals as in some earlier versions. Instead it keeps a matrix of optimal factors that can be converted to the matrix of optimum intervals (as in the formula from Point 1). The matrix of optimal factors OF used in Point 1 has been derived from the mathematical model of forgetting and from similar matrices built on data collected in years of repetitions in collections created by a number of users. Its initial setting corresponds with values found for a less-than-average student. During repetitions, upon collecting more and more data about the student’s memory, the matrix is gradually modified to make it approach closely the actual student’s memory properties. After years of repetitions, new data can be fed back to generate more accurate initial OF matrix. In SuperMemo 17, this matrix can be viewed in 3D with Tools : Statistics : Analysis : 3-D Graphs : O-Factor Matrix
- Item difficulty: The absolute item difficulty factor ( A-Factor), denoted AF in Point 1, expresses the difficulty of an item (the higher it is, the easier the item). It is worth noting that AF=OF[2,AF]. In other words, AF denotes the optimum interval increase factor after the second repetition. This is also equivalent with the highest interval increase factor for a given item. Unlike E-Factors in Algorithm SM-6 employed in SuperMemo 6 and SuperMemo 7, A-Factors express absolute item difficulty and do not depend on the difficulty of other items in the same collection of study material
- Deriving OF matrix from RF matrix: Optimum values of the entries of the OF matrix are derived through a sequence of approximation procedures from the RF matrix which is defined in the same way as the OF matrix (see Point 1), with the exception that its values are taken from the real learning process of the student for who the optimization is run. Initially, matrices OF and RF are identical; however, entries of the RF matrix are modified with each repetition, and a new value of the OF matrix is computed from the RF matrix by using approximation procedures. This effectively produces the OF matrix as a smoothed up form of the RF matrix. In simple terms, the RF matrix at any given moment corresponds to its best-fit value derived from the learning process; however, each entry is considered a best-fit entry on its own, i.e. in abstraction from the values of other RF entries. At the same time, the OF matrix is considered a best-fit as a whole. In other words, the RF matrix is computed entry by entry during repetitions, while the OF matrix is a smoothed copy of the RF matrix
- Forgetting curves: Individual entries of the RF matrix are computed from forgetting curves approximated for each entry individually. Each forgetting curve corresponds with a different value of the repetition number and a different value of A-Factor (or memory lapses in the case of the first repetition). The value of the RF matrix entry corresponds to the moment in time where the forgetting curve passes the knowledge retention point derived from the requested forgetting index. For example, for the first repetition of a new item, if the forgetting index equals 10%, and after four days the knowledge retention indicated by the forgetting curve drops below 90% value, the value of RF[1,1] is taken as four. This means that all items entering the learning process will be repeated after four days (assuming that the matrices OF and RF do not differ at the first row of the first column). This satisfies the main premise of SuperMemo, that the repetition should take place at the moment when the forgetting probability equals 100% minus the forgetting index stated as percentage. In SuperMemo 17, forgetting curves can be viewed with Tools : Statistics : Analysis : Forgetting Curves (or in 3-D with Tools : Statistics : Analysis : 3-D Curves):Figure: Tools : Statistics : Analysis : Forgetting Curves for 20 repetition number categories multiplied by 20 A-Factor categories. In the picture, blue circles represent data collected during repetitions. The larger the circle, the greater the number of repetitions recorded. The red curve corresponds with the best-fit forgetting curve obtained by exponential regression. For ill-structured material the forgetting curve is crooked, i.e. not exactly exponential. The horizontal aqua line corresponds with the requested forgetting index, while the vertical green line shows the moment in time in which the approximated forgetting curve intersects with the requested forgetting index line. This moment in time determines the value of the relevant R-Factor, and indirectly, the value of the optimum interval. For the first repetition, R-Factor corresponds with the first optimum interval. The values of O-Factor and R-Factor are displayed at the top of the graph. They are followed by the number of repetition cases used to plot the graph (i.e. 21,303). At the beginning of the learning process, there is no repetition history and no repetition data to compute R-Factors. It will take some time before your first forgetting curves are plotted. For that reason, the initial value of the RF matrix is taken from the model of a less-than-average student. The model of average student is not used because the convergence from poorer student parameters upwards is faster than the convergence in the opposite direction. The Deviation parameter displayed at the top tells you how well the negatively exponential curve fits the data. The lesser the deviation, the better the fit. The deviation is computed as a square root of the average of squared differences (as used in the method of least squares).Figure: 3D representation of the family of forgetting curves for a single item difficulty and varying memory stability levels (normalized for U-Factor).Figure: Cumulative forgetting curve for learning material of mixed complexity, and mixed stability. The graph is obtained by superposition of 400 forgetting curves normalized for the decay constant of 0.003567, which corresponds with recall of 70% at 100% of the presented time span (i.e. R=70% on the right edge of the graph). 401,828 repetition cases have been included in the graph. Individual curves are represented by yellow data points. Cumulative curve is represented by blue data points that show the average recall for all 400 curves. The size of circles corresponds with the size of data samples.
- Deriving OF matrix from the forgetting curves: The OF matrix is derived from the RF matrix by:
- fixed-point power approximation of the R-Factor decline along the RF matrix columns (the fixed point corresponds to second repetition at which the approximation curve passes through the A-Factor value),
- for all columns, computing D-Factor which expresses the decay constant of the power approximation,
- linear regression of D-Factor change across the RF matrix columns, and
- deriving the entire OF matrix from the slope and intercept of the straight line that makes up the best fit in the D-Factor graph. The exact formulas used in this final step go beyond the scope of this illustration.
- Item difficulty: The initial value of A-Factor is derived from the first grade obtained by the item, and the correlation graph of the first grade and A-Factor ( G-AF graph). This graph is updated after each repetition in which a new A-Factor value is estimated and correlated with the item’s first grade. Subsequent approximations of the real A-Factor value are done after each repetition by using grades, OF matrix, and a correlation graph that shows the correspondence of the grade with the expected forgetting index ( FI-G graph). The grade used to compute the initial A-Factor is normalized, i.e. adjusted for the difference between the actually used interval and the optimum interval for the forgetting index equal 10%
- Grades vs. expected forgetting index correlation: The FI-G graph is updated after each repetition by using the expected forgetting index and actual grade scores. The expected forgetting index can easily be derived from the interval used between repetitions and the optimum interval computed from the OF matrix. The higher the value of the expected forgetting index, the lower the grade. From the grade and the FI-G graph (see: FI-G graph in Tools : Statistics : Analysis : Graphs), we can compute the estimated forgetting index which corresponds to the post-repetition estimation of the forgetting probability of the just-repeated item at the hypothetical pre-repetition stage. Because of the stochastic nature of forgetting and recall, the same item might or might not be recalled depending on the current overall cognitive status of the brain; even if the strength and retrievability of memories of all contributing synapses is/was identical! This way we can speak about the pre-repetition recall probability of an item that has just been recalled (or not). This probability is expressed by the estimated forgetting index
- Computing A-Factors: From (1) the estimated forgetting index, (2) length of the interval and (3) the OF matrix, we can easily compute the most accurate value of A-Factor. Note that A-Factor serves as an index to the OF matrix, while the estimated forgetting index allows one to find the column of the OF matrix for which the optimum interval corresponds with the actually used interval corrected for the deviation of the estimated forgetting index from the requested forgetting index. At each repetition, a weighted average is taken of the old A-Factor and the new estimated value of the A-Factor. The newly obtained A-Factor is used in indexing the OF matrix when computing the new optimum inter-repetition interval
To sum it up. Repetitions result in computing a set of parameters characterizing the memory of the student: RF matrix, G-AF graph, and FI-G graph. They are also used to compute A-Factors of individual items that characterize the difficulty of the learned material. The RF matrix is smoothed up to produce the OF matrix, which in turn is used in computing the optimum inter-repetition interval for items of different difficulty ( A-Factor) and different number of repetitions (or memory lapses in the case of the first repetition). Initially, all student’s memory parameters are taken as for a less-than-average student (less-than average yields faster convergence than average or more-than-average), while all A-Factors are assumed to be equal (unknown).
1997: Employing neural networks
Neural Networks: Budding interest
In the mid-1980s, I read Michael Arbib’s ” Brains, Machines and Mathematics“. It consolidated my view of the brain as an efficient computing machine.
For anyone with an interest in how the brain works, and this is almost everyone, neural networks are naturally fascinating. While studying computer science, I gained a new, computational perspective of the brain and the neural networks. As neural networks have an uncanny capacity to do their own modelling, it may seem natural to employ them to study memory data to provide answers on how memory works. However, neural networks have one major shortcoming, they do not easily share their findings. It is a bit like the problem with the brain itself, it can do magic things and yet it is hard to say what is actually happening inside. It is fun to write neural network software, I dabbled in that in 1989. It is a bit less fun to see a neural network in action.
The algebraic approach to SuperMemo outstripped neural networks for two reasons: (1) my questions about memory always seemed too simple to involve neural networks, and (2) networks need data, which need learning, which needs an algorithm, which needs answering simple questions. In this chicken-and-egg race, my brain was always a step ahead of what I might figure out from available data with a neural network.
The superiority of the algebraic approach is obvious if you consider that the optimum interval can be found by just plotting a forgetting curve and employing regression to find the point where recall drops below 90%. This was even more extreme in my 1985 experiment where my “forgetting curve” was made of just 5 points. I was able to pick the one I just liked most. That was a pre-school exercise. No big guns needed.
In 1990, when working on the model of intermittent learning, I came closest to employing neural networks. After a 7-hour-long discussion with Murakowski on Jul 06, 1990, we concluded that a neural network could provide some answers. However, my computer was already churning data using algebraic hill-climbing methods. In essence, this is similar to feature extraction in neural networks. Once I got my answers, that motivation has been taken away.
Nevertheless, in the mid-1990s, we had more and more questions about the adaptability of the algorithm, and the possibility of employing neural networks. Those questions were primarily raised by those who do not understand SuperMemo much. The model behind SuperMemo is simple, the optimization tools are simple, and they work pretty well to our satisfaction. The very first computational approach, Algorithm SM-2, is used to this day. Human dissatisfaction with memory usually comes from unreasonable expectations that are built via school curricula, and our poor ability to formulate knowledge for healthy consumption. This last habit is also perpetuated by the push for cramming that we bring from school. SuperMemo algorithms cannot remedy that dissatisfaction with learning. They have always performed well, and the last 30 years delivered progress that can be measured mathematically, but which does not easily translate into an increase in the pleasure of learning.
Push for neural networks
In the 1990s, mail to SuperMemo World often included hints that the neural network approach would be superior. Even a decade of use of SuperMemo would not prevent a student from writing:
SuperMemo doesn’t take different user abilities and needs into account. Instead, it assumes that every learner is a “bad learner”. As such each learner will have the same repetition interval, its underlying algorithm is hardwired, but which might not be very efficient if you are a better/different learner. […] Neural networks take into account that there exist very different types of learners who need different optimum repetition intervals. When reviewing new words and by “telling” the programmes how well/bad they did the learner reveal more and more which type of learner they really are. After this feedback the programmes are able to adapt and optimise their underlying repetition intervals if necessary
Those words indicate lack of understanding of SuperMemo. SuperMemo does not use a “bad student model”. It only starts from shorter intervals before collecting first data about student’s memory. The choice of shorter intervals comes from a faster approximation of the optimum model. In other words, SuperMemo adapts to individual students, and the “less than average student model” might be attributed to the starting point before any data is collected.
In SuperMemo, the average student model is used only as an initial condition in the process of finding the model of the actual student’s memory.
In a finite-dimensional trajectory optimization, convergence is fastest for a good initial state guess. Although it is not the case in SuperMemo due to its simple 3-dimensional nature of the function of optimum intervals, in general case, the search for solutions may fail and the optimization will not work. Unlike the univalent matrices used in older SuperMemos for research purposes, a neural network algorithm would produce chaos without pre-training. This is why prior learning data are used to update the average or less-than-average student model used in SuperMemo for the maximum speed of convergence.
Note that this average student approach is even less significant in Algorithm SM-17 due to the use of best-fit approximations for multiple parameters and functions in the learning process (e.g. item difficulty, stability increase function, etc.). This means that SuperMemo will always make the best of available data (using our current best knowledge of memory models).
The approximate shape of the forgetting curve has been known for over a century now (see: Error of Ebbinghaus forgetting curve). SuperMemo collects precise data on the shape of forgetting curves for items of different difficulty and different memory stability. From forgetting curves, SuperMemo easily derives the optimum interval. The data comes from only one student and each repetition contributes to the precision of the computation. In other words, with every minute you spend with SuperMemo, the program knows you better and better. Moreover, it knows you well enough after a month or two. You never need to worry about the efficiency of the algorithm.
There is an aura of mystique around neural networks. They are supposed to reveal hidden properties of the studied phenomena. It is easy to forget that networks can fail easily when they are fed with wrong information or with some vital information missing. This was the case with the only functional neural network used in spaced repetition: MemAid by David Calinski.
The error in the design of MemAid network came from using Interval + Repetition Count on the input to represent the status of memory, while these two variables do not correspond with the Stability : Retrievability pair. Stability and Retrievability have been proven necessary to represent the status of a long-term memory trace. In other words, the network does not get all the information it needs to compute the optimum interval. A better design would code the entire repetition history, e.g. with the use of stability and retrievability variables. Full repetition history is needed to account for the spacing effect of massed presentation or a significant boost in stability for passing grades in delayed repetitions. Calinski’s design would, however, meet basic requirements for learning in “optimum” intervals with few departures from the rules of spaced repetition (as much as Algorithm SM-2).
Is SuperMemo inflexible?
It is not true that SuperMemo is prejudiced while a neural network is not. Nothing prevents the optimization matrices in SuperMemo to depart from the memory model and produce an unexpected result. It is true that over years, with more and more knowledge of how memory works, the algorithm used in SuperMemo has been armed with restrictions and customized sub-algorithms. None of these was a result of a wild guess though. The progression of “prejudice” in SuperMemo algorithms is only a reflection of findings from the previous years. The same would inevitably affect any neural network implementation if it wanted to maximize its performance.
It is also not true that the original pre-set values of optimization matrices in SuperMemo are a form of prejudice. These are an equivalent of pre-training in a neural network. A neural network that has not been pre-trained will also be slower to converge onto the optimum model. This is why SuperMemo is “pre-trained” with the model of an average student.
The rate of interval increase is determined by the matrix of optimum intervals and is by no means constant. Moreover, the matrix of optimum intervals changes in time depending on the user’s performance. You may have an impression of a fixed or rigid algorithm only after months or years of use (the speed of change is inversely proportional to the available learning data). This convergence reflects the invariability of the human memory system. It does not matter if you use the algebraic or neural approach to the optimization problem. In the end, you will arrive at the spaced repetition function that reflects the true properties of your memory. In that light, the speed of convergence should be held as a benchmark of the algorithm’s quality. In other words, the faster the interval function becomes “fixed”, the better.
Finally, there is another area where neural networks must either use the existing knowledge of memory models (i.e. carry a dose of prejudice) or lose out on efficiency. The experimental neural network SuperMemo, MemAid, as well as FullRecall have all exhibited an inherent weakness. The network achieves the stability when the intervals produce a desired effect (e.g. specific level of the measured forgetting index). Each time the network departs from the optimum model it is fed with a heuristic guess on the value of the optimum interval depending on the grade scored during repetitions (e.g. grade=5 would correspond with 130% of the optimum interval in SuperMemo NN or 120% in MemAid). The algebraic SuperMemo, on the other hand, can compute a difficulty estimate, use the accurate retention measurement, and produce an accurate adjustment of the value of the stability increase matrix. In other words, it does not guess on the optimal interval. It computes its exact value for that particular repetition. The adjustments to the memory matrices are weighted and produce a stable non-oscillating convergence. In other words, it is the memory model that makes it possible to eliminate the guess factor. With that respect, the algebraic SuperMemo is less prejudiced than the neural network SuperMemo.
Futility of the fine-tuning the spaced repetition algorithm
Algorithm SM-17 is a major step forward, however, many users will not notice the improvement and stick with the older algorithms. This perception problem led to the “SM3+ myth”, which I tried to dispel in this article. At the same time, the value of the new algorithm for further progress in research is astronomical. In other words, there is a big dissonance between practical needs and theoretical needs. My words in an interview for Enter, 1994, still ring true:
We have already seen that evolution speaks for SuperMemo, findings in the field of psychology coincide with the method, and that facts of molecular biology and conclusions coming from Wozniak’s model seem to go hand in hand. Here is the time to see how the described mechanisms have been put to work in the program itself. In the course of repetitions, SuperMemo plots the forgetting curve for the student and schedules the repetition at the moment where the retention, i.e. proportion of remembered knowledge, drops to a previously defined level. In other words, SuperMemo checks how much you remember after a week and if you remember less than desired it asks you to make repetitions in intervals less than one week long. Otherwise, it checks the retention after a longer period and increases the intervals accordingly. A little kink to this simple picture comes from the fact that items of different difficulty have to be repeated at different intervals, and that the intervals increase as the learning process proceeds. Moreover, the optimum inter-repetition intervals have to be known for an average individual, and these must be used before the program can collect data about the real student. There must be obviously the whole mathematical apparatus involved to put the whole machinery at work. All in all, Wozniak says that there have been at least 30 days in his life when he had an impression that the algorithms used in SuperMemo have significantly been upgraded. Each of the cases seemed to be a major breakthrough. The whole development process was just a long succession of trials and errors, testing, improving, implementing new ideas, etc. Unfortunately, those good days are over. There have not been any breakthrough improvement to the algorithm since 1991. Some comfort may come from the fact that since then the software started developing rapidly providing the user with new options and solutions. Can SuperMemo then be yet better, faster, more effective? Wozniak is pessimistic. Any further fine-tuning of the algorithms, applying artificial intelligence or neural networks would be drowned in the noise of interference. After all, we do not learn in isolation from the world. When the program schedules the next repetition in 365 days, and the fact is recalled by chance at an earlier time, SuperMemo has no way of knowing about the accidental recollection and will execute the repetition at the previously planned moment. This is not optimal, but it cannot be remedied by improving the algorithm. Improving SuperMemo now is like fine tuning a radio receiver in a noisy car assembly hall. The guys at SuperMemo World are now less focused on science. In their view, after the scientific invention, the time has come for the social invention of SuperMemo.
Dreger’s Neural Network Project
On May 20, 1997, my net buddy from the pre-web BBS era, Bartek Dreger, came up with a great idea. He would also write his Master’s Thesis about SuperMemo at Institute of Computer Science at Poznan University of Technology. That would be 8 years after my own, except he would use neural networks to see how they performed. Despite being nearly two decades younger, his plan was to try this project in the same great Węglarz operation research team I mention often elsewhere in this text. As early as in 1990, Dr Nawrocki came up with the idea to use neural networks to improve SuperMemo. The great mind of Prof. Roman Słowiński was to be the supervisor. This could really work.
By June 1997, another of my net buddies, Piotr Wierzejewski, joined the project. Then 3 more computer science students climbed aboard. It was a lovely team of five young brains with a combined age of 100. Soon the project was extended by the idea of on-line SuperMemo nicknamed: WebSorb (for the absorption of knowledge from the web). As it often happens in enthusiastic young teams, we started putting too much on the plate, and in the end, only a fraction of the goals has been attained. Only the on-line SuperMemo idea kept evolving and branching out in a meandering fashion with several mini-projects born and dying (e.g. e-SuperMemo, Quizer, Super-Memorizer, Memorathoner, etc.) until the emergence of 3GEMs that became supermemo.net that ultimately evolved into today’s supermemo.com.
The greatest advantage of youth in similar projects is creativity and passion. The greatest obstacle is schooling, and later, other obligations, including having children. This fantastic brain trust fell victim to the ages old problem of school: converting a project born in passion into a project that became a school chore with deadlines, reports, tests, exams, and grades. As explained here, SuperMemo was also born in that risky school environment. The key to success is the fight for freedom. Bondage destroys passions. The idea of SuperMemo survived the pressure of schooling because of my push for educational freedom.
Neural Network SuperMemo : Why memory model is vital in SuperMemo algorithms
Feature extraction proposed for spaced repetition neural networks is based on a well-proven existence of two components of long-term memory described here.
The two memory variables are sufficient to represent the status of an atomic memory trace in learning. Those variables make it possible to compute optimum intervals and account for the spacing effect. The function of increased memory stability for delayed repetitions is also known. For those reasons, a simple optimization algorithm makes it easy and fast to determine optimum repetition spacing in SuperMemo. A neural network would need to code the full repetition history for each item and the most obvious coding choices are memory stability (S) and memory retrievability (R). In other words, the same assumptions underlie the design of repetition spacing algorithms: algebraic or neural. Needless to say, the algebraic solution is easy and fast. It converges fast. It requires no pre-training (memory model is encapsulated in the matrix of optimum intervals).
A neural network working with full repetition histories will produce the same outcome as a hill-climbing algorithm employed in building stability of memory. Hill-climbing is simply a better/faster tool for the job. It will carry the same limitations as neural networks, i.e. the answers will be as good as the question posed.
Neural Network SuperMemo: Design
With Bartek Dreger we designed a simple ANN system for handling the spaced repetition problem (Dec 1997). Note that this project would not be possible without the expertise of Dr Krzysztof Krawiec who was helpful in polishing the design:
Archive warning: Why use literal archives?
The repetition spacing problem consists in computing optimum inter-repetition intervals in the process of human learning. The intervals are computed for individual pieces of information (later called items) and for a given individual. The entire input data are grades obtained by the student in repetitions of items in the learning process. This problem has until now be most effectively solved by means of a successive series of algorithms known commercially as SuperMemo and developed by Dr. Wozniak at SuperMemo World, Poland. Wozniak’s model of memory used in developing the most recent version of the algorithm ( Algorithm SM-8) cannot be considered as the ultimate algebraic description of human long-term memory. Most notably, the relationship between the complexity of the synaptic pattern and item difficulty is not well understood. More light on this relationship might be shed once a neural network is employed to provide adequate mapping between the memory status, grading and the item difficulty.
Using current state-of-the-art solutions, the technical feasibility of a neural network application in a real-time learning process seems to depend on the appropriate application of the understanding of the learning process to adequately define the problems that will be posed to the neural network. It would be impossible to expect the network to generate the solution upon receiving the input in the form of the history of grades given in the course of repetitions of thousands of items. The computational and space complexity of such an approach would naturally run well beyond the network’s ability to learn and respond in real time.
Using Wozniak’s model of two components of long-term memory we postulate that the following neural network solution might result in fast convergence and high repetition spacing accuracy.
The two memory variables needed to describe the state of a given engram are retrievability (R) and stability (S) of memory ( Wozniak, Gorzelańczyk, Murakowski, 1995). The following equation relates R and S:
(1) R=e -k/S*t
where:
- k is a constant
- t is time
By using Eqn (1) we conclude about changes of retrievability in time at a given stability, as well as we can determine the optimum inter-repetition interval for given stability and given forgetting index.
The exact algebraic shape of the function that describes the change of stability upon a repetition is not known. However, experimental data indicate that stability usually increases from 1.3 to 3 times for properly timed repetitions and depends on item difficulty (the greater the difficulty the lower the increase). By providing the approximation of the optimum repetition spacing taken from experimental data as produced by optimization matrices of Algorithm SM-8, the neural network can be pre-trained to compute the stability function:
(2) S i+1=f s(R,Si,D,G)
where:
- S i is stability after the i-th repetition
- R is retrievability before repetition
- D is item difficulty
- G is grade given in the i-th repetition
The stability function is the first function to be determined by the neural network. The second one is the item difficulty function with analogous input parameters:
(3) D i+1=f d(R,S,Di,G)
where:
- D i is item difficulty approximation after the i-th repetition
- R is retrievability before repetition
- S is stability after the i-th repetition
- G is grade given in the i-th repetition
Consequently, a neural network with four inputs (D, R, S and G) and two outputs (S and D) can be used to encapsulate the entire knowledge needed to compute inter-repetition intervals (see: Implementation of the repetition spacing neural network).
The following approach will be taken in order to verify the feasibility of the aforementioned approach:
- Pretraining of the neural network will be done on the basis of approximated S and D functions derived from functions used in Algorithm SM-8 and experimental data collected thereof
- Such a pretrained network will be implemented as a SuperMemo Plug-In DLL that will replace standard sm8opt.dll used by SuperMemo 8 for Windows. The teaching of the network will continue in a real learning process in alpha testing of the neural network DLL. A procedure designed specifically for the purpose of the experiment will be used to provide cumulative results and a resultant neural network. The procedure will use neural networks used in alpha testing for training the network that will take part in beta-testing. The alpha-testing networks will be fed with a matrix of input parameters and their output will be used in as training data for the resultant network
- In the last step, beta-testing of the neural network will be open to all volunteers over the Internet directly from the SuperMemo Website. The volunteers will only be asked to submit their resultant networks for the final stage of the experiment in which the ultimate network will be developed. Again, the beta-testing networks will all be used to train the resultant network. Future users of neural network SuperMemo (if the project appears successful) will obtain a network with a fair understanding of the human memory and able to further refine its reactions to the interference of the learning process with day-to-day activities of a particular student and particular study material.
The major problem in all spacing algorithms is the delay between comparing the output of the function of optimum intervals with the result of applying a given inter-repetition interval in practise. On each repetition, the state of the network from the previous repetition must be remembered in order to generate the new state of the network. In practise, this equates to storing an enormous number of network states in-between repetitions.
Luckily, Wozniak’s model implies that functions S and D are time-independent (interestingly, they are also likely to be user-independent!); therefore, the following approach may be taken for simplifying the procedure:
| Time moment | T1 | T2 | T3 |
|---|---|---|---|
| Decision | I 1N 1O 1=N 1(I 1) | I 2N 2O 2=N 2(I 2) | I 3N 3O 3=N 3(I 3) |
| Result of previous decision | O* 1E 1=O* 1-O 1 | O* 2E 2=O* 2-O 2 | |
| Evaluation for teaching | O’ 1=N 2(I 1)E’ 1=O* 1-O’ 1 | O’ 2=N 3(I 2)E’ 2=O* 2-O’ 2 |
Where:
- E i is an Error bound with O i (see error correction for memory stability and error correction for item difficulty)
- E’ i is an Error bound with O’ i
- I i are input data at T i
- N i is the network state at T i
- O i is an output decision of N i being given I i, that is the decision after i-th repetition made at T i
- O* i is an optimum output decision, that should be obtained at T i instead of O i; it can be computed from the grade and O i (the grade indicates how O i should have changed to obtain better approximation)
- O’ i is an output decision of N i+1 given I i, that is the decision after i-th repetition that would be made at T i+1
- T i is time of the i-th repetition of a given item
The above approach requires only I i-1 to be stored for each item between repetitions taking place at T i-1 and T i with substantial saving to the amount of data stored during the learning process (E’ i is as valuable for training as E i). This way the proposed solution is comparable for its space complexity with the Algorithm SM-8! Only one (current) state of the neural network has to be remembered throughout the process.
These are the present implementation assumptions for the discussed project:
- neural network: unidirectional, layered, with resilient back-propagation; an input layer with four neurons, an output layer with two neurons, and two hidden layers (15 neurons each)
- item difficulty interpretation: same as in Algorithm SM-8, i.e. defined by A-Factor
- each item stores: Last repetition date, Stability (at last repetition), Retrievability (at last repetition), Item difficulty, Last grade
- default forgetting index: 10%
- network DLL input (at each repetition): item number and the current grade
- network DLL output (at each repetition): next repetition date
- neural network DLL implementation language: C++
- neural network DLL shell, SuperMemo 98 for Windows (same as the 32-bit SM8OPT.DLL shell)
Neural Network SuperMemo: Implementation
The network has practically been given the spaced repetition algorithm on a silver platter. Its only role would be to fine-tune the performance over time. This is exactly what all SuperMemo algorithms do as of Algorithm SM-5. In that sense, the design did not ask the network for a discovery. It asked for improvements upon the discovery. The model was wired in into the design.
Archive warning: Why use literal archives?
Basic assumption
The state of memory will be described with only two variables: retrievability (R) and stability (S) ( Wozniak, Gorzelańczyk, Murakowski, 1995). The following equation relates R and S:
(1) R=e -k/S*t
where:
- k is a constant
- t is time
For simplicity, we will set k=1 to univocally define stability.
Input and output
The following functions are to be determined by the network:
(2) S i+1=f s(R, S i, D, G)
(3) D i+1=f d(R, S, D i, G)
The neural network is supposed to generate stability (S) and item difficulty (D) on the output given R, S, D and G on the input:
(4) (Ri, Si, Di, Gi) => (D i+1,S i+1)
where:
- R i is retrievability before the i-th repetition
- S i is stability before the i-th repetition
- S i+1 is stability after the i-th repetition
- D i is item difficulty before the i-th repetition
- D i+1 is item difficulty after the i-th repetition
- G i is grade given in the i-th repetition
Error correction for difficulty D
Target difficulty will be defined as in Algorithm SM-8 as the ratio between second and first intervals. The neural network plug-in (NN.DLL) will record this value for all individual items and use it in training the network:
(5) D o=I 2/I 1
where:
- D o is guiding difficulty used in error correction (the higher the D o, the less the difficulty)
- I 1 is the first optimum interval computed for the item in question (same for all items)
- I 2 is the second optimum interval computed for the item
Important! The optimum intervals I 1 and I 2 are not the ones proposed by the network before its verification but the ones used in error correction after the proposed interval had already been executed and verified (see error correction for stability S)!
The initial value of difficulty will be set to 3.5, i.e. D 1=3.5. This is for similarity with Algorithm SM-8 only. As initial difficulty is not known, it cannot be used to determine the first interval. After scoring the first grade the error correction is still impossible due to the fact that second optimum interval is not known. Once it is known, D o can be used for error correction of D on the output.
To avoid convergence problems in the network, the following formula will be used to determine the correct output on D:
(6) D opt=0.9*D i+0.1*D o
where:
- D opt is difficulty used in error correction after the i-th repetition
- D i is difficulty before the i-th repetition
- D o is guiding difficulty from Eqn (5)
The convergence factor of 0.9 in Eqn (6) is arbitrary and may change depending on the network performance.
Error correction for stability S
The following formula, derived from Eqn (1) for forgetting index equal 10% and k=1, makes it easy to convert stability and the optimum interval: I=-ln(0.9)*S
In the optimum case, the network should generate the requested forgetting index for each repetition. Variable forgetting index can easily be used once the stability S is known (see Eqn (1)). For simplicity then we will use forgetting index equal 10% in further analysis.
To accelerate the convergence, the network will measure forgetting index for 25 classes of repetitions. These classes are set by (1) five difficulty categories: 1-1.5, 1.5-2.5, 2.5-3.5, 3.5-5, and over 5, and (2) five interval categories: 1-5, 5-20, 20-100, 100-500 and over 500 days. We will denote the forgetting index measurements for these categories as FI(D m,I n). Additionally, the overall forgetting index FI tot will be measured and used in stability error correction.
The ultimate goal is to reach the forgetting index of 10% in all categories. The following formula will be used in error correction for stability:
(7) FI opt(m,n)=(10*FI tot+Cases(m,n)*FI(m,n))/(10+Cases(m,n))
where:
- FI opt(m,n) is forgetting index used in error correction after a repetition belonging to category (m,n)
- FI tot is the overall forgetting index measured in repetitions
- Cases(m,n) is the number of repetition cases used to measure the forgetting index in category (m,n)
The formula in Eqn (7) is supposed to shift the weight on error correction from the overall forgetting index to forgetting index recorded in given categories as soon as the number of cases in individual categories increases. Obviously, for Cases(m,n)=0, we have FI opt(m,n)=FI tot. For Cases(m,n)=10 the weights for overall and category FI balance, and for a large number of cases, FI opt(m,n) is approaching FI(m,n).
The following table illustrates the assumed relationship between FI opt(m,n), grades and the interval correction applied:
| Grade | 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| FI opt(m,n)>10% | 40% | 60% | 80% | no correction | no correction | no correction |
| FI opt(m,n)=10% | no correction | no correction | no correction | no correction | no correction | no correction |
| FI opt(m,n)<10% | no correction | no correction | no correction | 110% | 120% | 130% |
In SuperMemo, grades less than 3 are interpreted as forgetting, while grades equal 3 or more are understood as sufficient recall. That is why no correction is used for passing grades in case of satisfactory FI, and no correction is used for failing grades if FI is greater than requested. An exemplary correction for an excessive forgetting rate and grade=2 for applied interval of 10 days would be 80%. Consequently, the network will be instructed to assume Interval=8 as correct. Correct stability would then be derived from S=-8/ln(0.9) and used in error correction. The values of interval corrections are arbitrary but shall not undermine the convergence of the network. In case of unlikely stability problems, the corrections might be reduced (note that the environmental noise in the learning process will dramatically exceed the impact of ineffectively choosing the correction factors!). Similar corrections used to be applied in successive SuperMemo algorithms with encouraging results.
Border conditions
The following additional constraints will be imposed on the neural network to accelerate the convergence:
- interval increase in two successive repetition must be at least 1.1 (consequently, difficulty cannot be less than 1.1)
- interval increase cannot surpass 8 after the first repetition, and 4 in later repetitions
- the first interval must fall between 1 and 40 days
- difficulty measure cannot exceed 8
These conditions will not prejudice the network as they have been proven beyond reasonable doubt as true in the practice of using SuperMemo and its implementations over the last ten years.
Pretraining
In the pretraining stage, the following form of Eqns (2) and (3) will be used:
(8) D i+1:=D i+(0.1-(5-G)*(0.08+(5-G)*0.02))
(9) S i+1:=S i*D i*(0.5+1/i)
With D 1=3.5 and S 1=-3/ln(0.9).
Eqn (8) has been derived from Algorithm SM-2 (see E-Factor equation). Eqn (9) has been roughly derived from Matrix OF in Algorithm SM-8. D 1=3.5 corresponds with the same setting in Algorithm SM-8. S 1=-3/ln(0.9) corresponds with the first interval of 3 days and forgetting index 10%. The value of 3 days is close to an average across a wide spectrum of students and difficulty of the learning material.Pretraining will also use border conditions mentioned in the previous paragraph.
There were multiple problems with the neural network, implementation, bugs, convergence, interference, and the like. The only way to effectively study the network was to plug it in real SuperMemo and see how it works on real data. I came up with an idea of plug-in algorithms in a DLL. We could study algorithmic variants in the same shell. We tried out Algorithm SM-2, Algorithm SM-8 and now a neural network was to do the same. Unfortunately, that DLL implementation proved a step too far. Once the enthusiastic kids graduated, they soon dispersed, found jobs elsewhere, got married, and I never had a chance to try the plug-in in my own learning in my favorite shell, which was SuperMemo 9 at that time (aka SuperMemo 98).
Neural network SuperMemo was a student project with a sole intent to verify the viability of neural networks in spaced repetition. Needless to say, neural networks are a viable tool. Moreover, all imaginable valid optimization tools, given sufficient refinement, are bound to produce similar results to those currently accomplished by SuperMemo. In other words, as long as the learning program is able to quickly converge to the optimum model and produce the desired level of knowledge retention, the optimization tool used to accomplish the goal is of secondary importance.
Considering the number of problems at earlier stages, I doubt that successful plug-in would change my thinking about neural networks. I am a programmer and a tinkerer, I like to see what I create. Neural network appeared too black boxy to me. As for the team, they are all successful in their careers today. The kids have contributed to some other SuperMemo efforts later on. Youth is creative, youth is unpredictable, and I am glad we took on the project.
David Calinski and FullRecall
David Calinski (b. 1981) was one of the early youthful SuperMemo enthusiasts in the 1990s. He showed rich interest in accelerated learning, psychology, psychiatry, and beyond.
I quickly recognized his talents and was hoping to recruit him in some SuperMemo projects, incl. SuperMemo for Linux, however, many a genius like to walk alone. At some point, he switched from SuperMemo to his own application (FullRecall, see later), and from that point on, he would not abandon his project.
Our discussions about neural networks started in 2001. David was a fan of SuperMemo, however, he also admitted to have never truly studied the algorithm. This led to a criticism:
I don’t know the exact details of SM algorithm(s) (I never was much interested in it), but important here is the main idea. Algorithm in SM gets some data (e.g. number of repetitions, difficulty of item, current grade, etc. etc.) and returns next optimal interval it calculated. This algorithm, even if it’s “smart” and corrects itself somehow, will be still dumb – it won’t correct itself more than was designed for.
He is right, Algorithm SM-17 is inherently bound to the two component model of long-term memory, however, this is a happy marriage. The bond can only be broken by counter-evidence that hasn’t come in three decades thus far.
David’s stance is entirely justifiable. It is all about modelling and prior knowledge. For David, Algorithm SM-8 was complex. Neural networks seem like a simple way to take away the complexity. To me, my own algorithm is as simple as the multiplication table. That modelling difference often leads to cognitive divergence and this is a good thing. Without those differences, we would know much less about neural networks in spaced repetition today!
I wrote to David in 2004: “Further improvements to the algorithm used in SuperMemo are not likely to result in further acceleration of learning. However, there is still scope for improvement for handling unusual cases such as dramatically delayed repetitions, massed presentation, handling items whose contents changed, handling semantic connections between items, etc. Interestingly, the greatest progress in the algorithm is likely to come from a better definition of the model of human long-term memory. In particular, the function describing changes in memory stability for different levels of retrievability is becoming better understood. This could dramatically simplify the algorithm. Simpler models require fewer variables and this simplifies the optimization. The algorithm based on stability and retrievability of memory traces could also result in better handling of items with low retrievability. However, as unusual item cases in the learning process form a minority, and testing a new algorithm would take several years, it is not clear if such an implementation will ever be undertaken”.
David developed his own neural network, MemAid. Later he converted it into a commercial product. The move from free to commercial was hard as users tend to prefer a drop in prices, for obvious reasons. Despite all ups and downs, David persisted, and his DIY tinkerer and passion for science and programming always gave him an upper hand. Like Anki, he tried to keep his program cross-platform which imposed some limits and demands on simplicity. In his words: “I love speed and lack of borders, lack of dependency on just one solution, system, computer, etc.”
Today FullRecall is free. See the changelong.
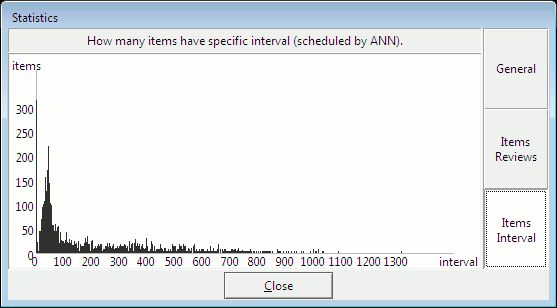
Figure: Interval distribution in FullRecall. Repetitions scheduled with the help of a neural network
The open-source MemAid project closed in 2006, but FullRecall continued. So did another project inspired by MemAid: Mnemosyne. Mnemosyne, however, opted for their own version of Algorithm SM-2. To this day, Mnemosyne generates data that can be used by spaced repetition enthusiasts or researchers at The Mnemosyne Project.
Like Calinski, Peter Bienstman is skeptical of newer algorithms: “SuperMemo now uses SM-11. However, we are a bit skeptical that the huge complexity of the newer SM algorithms provides for a statistically relevant benefit. But, that is one of the facts we hope to find out with our data collection.”
“Statistically relevant benefit” depends on the criteria. For users, the actual algorithm may be secondary. For research, Algorithm SM-17 is a goldmine (as much as data that all programs like Mnemosyne can generate).
Why is the neural network in FullRecall flawed?
The two memory variables are both necessary and sufficient to represent an atomic memory in spaced repetition. Moreover, the two variables can be used to account for spacing effect in massed presentation. They can also explain the benefit of high forgetting index for long-term retention as discussed here. Those two variables of long-term memory which we named: stability and retrievability are necessary to represent the status of memory. Any neural network that wants to find patterns in the relationship between spacing and recall must receive the full status of memory on its input otherwise it won’t ever compute the optimum spacing. That status may have a form of the full history of repetition. It may also be the stability : retrievability pair (if it can be computed). It may also be any other code over the history of repetitions from which the status of memory can be computed.
The design of the FullRecall network does not meet those criteria:
- input: last_interval_computed_by_ann [0-2048 days] (zero if this is not a review, but a first presentation)
- input: real_interval_since_last_review [0-2048 days] (same comment as above)
- input: number_of_repetitions_of_an_item_so_far [0-128]
- input: current_grade [0-5, 5 is the best]
- output that ANN gives us: new_interval [0-2048]
Neither interval nor repetitions count can reflect memory stability or retrievability. You can obtain high repetition counts in massed presentation subject to spacing effect with a negligible increase in memory stability. At the same time, long intervals for suboptimum schedules may result in low values for both stability and retrievability. In short, for the same interval, the status of memory will depend on the distribution of repetitions in time.
This can be shown with an example: for 10 repetitions, and 1000 days, 9 repetitions in 9 days combined with 991 day interval will produce stability approaching zero (assuming no interference). At the same time, for the same pair of inputs, optimally spaced repetition can bring retrievability of nearly 100% and stability that allows of optimum intervals close to 1000 days.
The only scenario where the network might perform well is where the user adheres precisely to the optimum spaced repetition schedule. This, in turn, can only come from a network that has been pre-trained, e.g. with Algorithm SM-2. In this scenario, the network will be unstable and won’t converge on the optimum due to the fact that all departures from the optimum schedule, incl. those caused by network error will shift the state of the network away from the original state in which it was still able to compute memory status from its inputs.
Stability and retrievability are sufficient in the idealized case for a unitary monosynaptic association. In real life, the semantic network involved in the association is likely to involve a number of such ideal unitary memories. This is why SuperMemo uses the concept of absolute item difficulty. In Algorithm SM-17, the absolute item difficulty is determined by the maximum increase in memory stability for the first optimally scheduled review at the default forgetting index of 10%. The FullRecall network does not receive any reliable measure of item difficulty either. This will compound the network’s inefficiency.
The FullRecall network is said to work pretty well, according to users reports. In the light of the present analysis, the network might employ well-chosen boundary conditions, however, this would be equivalent to returning to Algorithm SM-2 employed in older versions of SuperMemo. Needless to say, that old SuperMemo algorithm is more biased and less plastic than newer matrix-based algebraic versions employed in SuperMemo.
If the FullRecall network is pre-trained, e.g. with the help of Algorithm SM-2, and the student sticks rigorously to his or her repetition, the network might work ok as the interval correlates well with memory stability, esp. if the information is enhanced by the number of repetitions. However, without appropriate boundary conditions, in incremental reading, the network would certainly fail as it might receive false memory status information. Depending on the scenario, the same Repetitions : Interval pair may occur for Stability=0 and for maximum stability corresponding with lifetime memories. Similarly, the retrievability may also vary in the 0-1 range for the same input pair in the network. For example, frequent subset review before an exam followed by a longer break in learning (e.g. caused by overflow) may correspond with very low stability and retrievability despite providing the same input as a correctly executed series of spaced reviews in the same period (with high stability and retrievability above 0.9). In incremental reading, overload, auto-postpone, item advance, subset review, and spacing effect would be invisible to the network.
Assuming good design, the flaws of FullRecall will then only show in intermitted learning, which may trigger boundary conditions. It should not detract from the value of the software itself. It is only to emphasize that neural network design is not easy, and may turn out inferior.
In short, its inputs do not reflect all necessary information needed for computing optimum intervals. In particular, repetition count is a very poor measure of memory stability or retrievability. A better approach would be to code the entire history of repetitions or compute the status of memory with the use of stability and retrievability variables. Both stability and retrievability must be computable from the network input.
Future of neural networks in SuperMemo
In our discussions with Calinski (in 2001), I summarized my reservations and vowed to continue on the same old “conservative” path. 17 years later, I am glad. There has not been much progress in the area of employing neural networks in spaced repetition. It might be the fact that SuperMemo itself is an inhibitor of progress. In the meantime, however, Algorithm SM-17 has revealed further potential for improvements in spaced repetition and understanding human memory. Time permitting, there will still be progress.
SuperMemo will continue with its algebraic algorithms for the following reasons:
- Known model: Neural networks are superior in cases where we do not know the underlying model of the mapped phenomena. The model of forgetting is well-known and makes it easy to fine-tune the algebraic optimization methods used in computing inter-repetition intervals. The well-known model also makes SuperMemo resistant to unbalanced datasets, which might plague neural networks, esp. in initial stages of learning. Last but not least, the validity of the two component model of memory has been proven in many ways and giving up the model while designing the network, in the name of stemming prejudice, would be wasteful. Such approach may have a research value only
- Overlearning: Due to case-weighted change in array values, optimization arrays used in SuperMemo are not subject to “overlearning”. No pretraining is needed, as the approximate shape of the function of optimal intervals is known in advance. There is no data representation problem, as all kinky data input will be “weighed out” in time
- Equivalence: Mathematically speaking, for continuous functions, n-input networks are equivalent to n-dimensional arrays in mapping functions with n arguments, except for the “argument resolution problem”. The scope of argument resolution problem, i.e. the finite number of argument value ranges, is strongly function dependent. A short peek at the optimization arrays displayed by SuperMemo indicates that the “argument resolution” is far better than what is actually needed for this particular type of function, esp. in the light of the substantial “noise” in data. Hill-climbing algorithms used in SuperMemo are reminiscent of the algorithms aimed at reweighing the networks
- Research: The use of matrices in SuperMemo makes it easy to see “memory in action”. Neural networks are not that well-observable. They do not effectively reveal their findings. You cannot see how a single forgetting curve affects the function of optimum intervals. This means that the black-box nature of neural networks makes them less interesting as a memory research tool
- Convergence: The complexity of the algorithm does not result from the complexity of the memory model. Most of the complexity comes from the use of tools that are supposed to speed up the convergence of the optimization procedure without jeopardizing its stability. This fine-tuning is only possible due to our good knowledge of the underlying memory model, as well as actual learning data collected over years that help us precisely determine best approximation function for individual components of the model
- Forgetting curve: The only way to determine the optimum interval for a given forgetting index is to know the (approximate) forgetting curve for a given difficulty class and memory stability. If a neural network does not attempt to map the forgetting curve, it will always oscillate around the value of the optimum interval (with good grades increasing that value, and bad grades decreasing it). Due to data noise, this is only a theoretical problem; however, it illustrates the power of using a symbolic representation of stability-retrievability-difficulty-time relationship instead of a virtually infinite number of possible forgetting curve data sets. If the neural network does not use a weighted mapping of the forgetting curve, it will never converge. In other words, it will keep oscillating around the optimum model. If the neural network weighs in the status history and/or employs the forgetting curve, it will take the same approach as the present SuperMemo algorithm, which was to be obviated by the network in the first place
In other words, neural networks could be used to compute the intervals, but they do not seem to be the best tool in terms of computing power, research value, stability, and, most of all, the speed of convergence. When designing an optimum neural network, we run into similar difficulties as in designing the algebraic optimization procedure. In the end, whatever boundary conditions are set in “classic” SuperMemo, they are likely to appear, sooner or later, in the network design (as can be seen in: Neural Network SuperMemo).
As with all function approximations, the choice of the tool and minor algorithmic adjustments can make a world of difference in the speed of convergence and the accuracy of mapping. Neural networks could find use in mapping the lesser known accessory functions that are used to speed up the convergence of the algebraic algorithm. For example, to this day, item difficulty estimate problem has not been fully cracked. We simply tell users to keep their knowledge simple, which is a universal recommendation from any educator aware of mnemonic limits of human memory.
1999: Choosing the name: “spaced repetition”
Quest for a good unique name
The term ” spaced repetition ” is very old and has been used for decades in the advertising industry and in behavioral research. However, its modern meaning based on the optimum review intervals has been established only when the name was used to stand for the SuperMemo method (as of 1999).
In the early days of SuperMemo World, we actively searched for a well-recognized scientific term to use when referring to ” the SuperMemo method” in scientific contexts. The company’s marketing strategy was to move away from a ” program developed by a student” to a ” program based on a scientific method“. Unfortunately, memory and learning literature was scant on publications other than short-term studies of the spacing effect with a notable exception of H. Bahrick’s research on the retention of Spanish vocabulary.
Memory researchers have investigated various ” repetition schedules” for ages. Sometimes they used intervals of minutes. Sometimes they used “intervening items” to separate review. Three review patterns have been most prevalent: (1) massed with many repetitions in short time, (2) distributed with repetitions dispersed in time, and (3) expanding with increasing interval. Spaced repetition relies on a progressively expanding schedule. Over decades, memory literature could not settle on a specific term to refer to the expanding schedule. Pimsleur used graduated intervals, Bjork used expanding rehearsal, Baddley used distributed practice, in my Master’s Thesis, I used progressive schedule, Pavlik uses more general optimal schedule that we know is progressive, etc.
A seminal article by Frank N. Dempster ” The Spacing Effect A Case Study in the Failure to Apply the Results of Psychological Research” (American Psychologist, 43, 627-634, 1988) gave an early boost to SuperMemo. The article deplored the fact that educators ignore the spacing effect in the pracise of learning. SuperMemo could fill the gap by providing a simple universal tool for spaced learning. Dempster freely used terms such as “spaced presentation”, “spaced reviews”, “spaced practise”, “spaced tests”, and even “spaced readings”, or “well-spaced presentations”.
We chose the term ” repetition spacing” to be used instead of ” the SuperMemo method“. The first-ever English language scholarly article describing computational spaced repetition (1994) still used the term ” repetition spacing“.
Choosing the name: spaced repetition
On Feb 3, 1999, inspired by an e-mail from a user of SuperMemo ( Tony D’Angelo), I reviewed literature using the keyword ” spaced repetition“. Upon that review, I got convinced that we should move from using the term ” repetition spacing” to ” spaced repetition“. The term ” spaced repetition” was equally obscure and rarely used, but had a better use count than ” repetition spacing“.
We decided that in future SuperMemos, the term ” spaced repetition” should be used instead of ” repetition spacing“. The first use of the term at supermemo.com probably came on Feb 4, 2000 in SuperMemo is useless
Over time, the term ” spaced repetition” has become more and more popular. In that light, SuperMemo can also take credit for making this generic scientific term take root in public’s mind with a specific association to optimum intervals in learning.
The future of the name: spaced repetition
As of 1999, largely due to our choice of the name, the term ” spaced repetition ” has consolidated its presence in texts referring to flashcard applications, incl. those based on the Leitner system. There is also a hope, the term will become dominant in scientific literature. All authors prefer to stick to the terminology they have used for years or decades. However, a great deal of terminological acceleration can be attributed to Wikipedia. The dominant term in there is spaced repetition, however, memory scientists tend to flock to spaced retrieval or distributed practice (which is a wider concept). There are also island entries like spaced learning that have been attributed by spambots to Paul Kelly (at the time headmaster at Monkseaton High School).
This confusion contributes to the disconnect between research and popular applications of spaced repetition, but the merger and unification are just a matter of time. Wikipedia uses a concept of proposed mergers. Scientists may oppose merging their “clean” versions with the popular version peppered with commercial links. However, such a merger is inevitable and good. There are scientists who investigate spaced repetition today who do not know the term spaced repetition, and never heard of SuperMemo. There are also engineers who work on spaced repetition algorithms who know very little of actual memory research in the field. Both problems can be reduced by unifying the terminology. Google will do the rest.
Unification of terminology under the banner of ” spaced repetition” will serve further research and popular applications
2005: Stability increase function
Why a simple idea could not materialize?
A perfect mathematical description of long-term memory is just about a corner. It may seem amazing today, but despite its simplicity, it took three long decades of starts and stops before a good model could emerge. In human endeavor, science is often a side effect of human curiosity while other burning projects often receive priority. The problem with science that it is blind, it says little of its secrets before they are uncovered. A moral of the story is that all governments and companies should spare no resources for good science. Science is a bit like SuperMemo, today it seems like the reward is little, but in the long-term, the benefits can be stunning.
Today we can almost perfectly describe memory with the toolset employed in Algorithm SM-17. The only limit on further progress in understanding memory is the imagination, availability of time, and the ability to pose the right questions. We have all the tools and we have a lot of data. We even have a nice portion of data combined with sleep logs that can now add a new dimension to the model: homeostatic readiness for learning, homeostatic fatigue and even the circadian factor.
An important moral of the story behind SuperMemo is that if you have an idea, put it to life (unless you have another better idea). The problem with ideas is that they may often seem a fraction as attractive as they are. I plotted my first forgetting curve in 1984, I forgot about it within a few months and recalled the fact 34 years later at the time when my whole life revolves around forgetting curves. Imagine the surprise! When I came up with the first spaced repetition algorithm, it took me over 2 years before I decided to recruit the first user. Without Tomasz Kuehn, SuperMemo for Windows might arrive 2-4 years later. Without Janusz Murakowski, vital big data: repetition history record in SuperMemo might have been delayed by 1-2 years. When incremental reading came to life in 2000, only I knew it was a monumental thing. However, it took me quite a while to appreciate the extent of that fact. Today, I know neural creativity is a breakthrough tool, but I am still using it half-heartedly and not as often as its simpler alternative: subset review.
1990: First hint
Algorithm SM-17 was in the making for nearly a quarter of a century. While preparing materials for this article, in my archive, I found a picture of a matrix named “new strength” with rows marked as “strength” and columns marked as “durability”. These were the original names for stability and retrievability used in the years 1988-1990. Like an old fossil, the paper tells me that the idea of Algorithm SM-17 must have been born around 1990.
Figure: A picture of a matrix named “new strength” with rows marked as “strength” and columns marked as “durability”. These were the original names for stability and retrievability used in the years 1988-1990. The paper suggests that the idea of Algorithm SM-17 must have been born around 1990.
From the very early beginnings of the two component model of memory, I wanted to build an algorithm around it. My motivation was always half-hearted. SuperMemo worked well enough to make this just a neat theoretical exercise. However, today I see that the algorithm provides data for a model that can answer many questions about memory. Some of those questions have actually never been asked (e.g. about subcomponents of stability). This is also similar to SuperMemo itself. It has always struggled because its value is hard to appreciate in theory. Practical effects are what changes the mind of good students most easily.
1993: Distraction
In 1993, my own thinking was an inhibitor of progress. Further explorations of the algorithm were secondary. They would not benefit the user that much. Memory modelling was pure blue sky research. See: Futility of fine-tuning the algorithm. At that time it was Murakowski who would push hardest for progress. He kept complaining that ” SuperMemo keeps leaking Nobel Prize value data“. He screamed at me with words verging on abuse: ” implement repetition histories now!“. It was simply a battle of priorities. We had a new Windows version of SuperMemo, the arrival of audio data, the arrival of CD-ROM technology, the arrival of solid competition, incl. at home where Young Digital Poland beat us to the title of the first CD-ROM title in our home country by a month or so. We still cherish the claim to the first Windows CD-ROM in Poland. It was actually still produced in the US, but the contents were made entirely in Poland around 100% pure Polish SuperMemo.
1996: Venture capital
In February 1996, all obstacles have been cleared and SuperMemo finally started collecting full repetition history data (at that time, it was still an option to prevent clogging lesser systems with unused data). My own data now reaches largely back to 1992-1993 as all items in February 1996 still had their last repetition easily identifiable from the interval. I even have quite a number of histories dating back to 1987. In my OCD for data, I recorded the progress of some specific items manually and was later able to complete repetition histories by manual editing. My own data is now, therefore, the longest spanning repetition history data in spaced repetition in existence. 30 years of data with a massive coverage for 22-25 years of learning. This is a goldmine.
On Sep 29, 1996, Sunday, in the evening, I devoted two hours to sketching the new algorithm based on the two component model of memory. It all seemed very simple and requiring little work. SuperMemo has just started collecting repetition histories, so I should have plenty of data at hand. Our focus switched from multimedia courses, like Cross Country, to easier projects, like Advanced English. It was a good moment, it seemed. Unfortunately, the next day we got a call from Antek Szepieniec who talked to investors in America with a dream to make SuperMemo World the first Polish company at NASDAQ. He excitedly prophesied his belief that there is a good chance for an injection of a few million dollars into our efforts from venture capital. That instantly tossed me into new roles and new jobs. Of bad things, this has delayed Algorithm SM-17 by two decades. Of good things, the concept of Hypermedia SuperMemo, aka Knowledge Machine, aka incremental reading has gained a great deal of momentum in terms of theory and design. Practice trumped science again.
2005: Theoretical approach
In 2000, with incremental reading, and then 2006 with priority queue, the need for the delay of repetitions, and the need for early review increased dramatically. This called for huge departures from the optimum. The old Algorithm SM-8 could not cope with that effectively. The function of optimum intervals had to be expanded into the dimension of time (i.e. retrievability). We needed a stability increase function.
One of the very interesting dynamics of progress in science is that the dendritic explorations of reality often require a critical brain mass to push a new idea through. In 2005, Biedalak and others were largely out of the loop busy with promoting SuperMemo as a business. I was on the way to a major breakthrough in incremental reading: handling overload. With the emergence of Wikipedia, it suddenly appeared that importing tons of knowledge requires little effort, but low-priority knowledge can easily overwhelm high-priority knowledge by sheer volume. Thus richness undermines the quality of knowledge. My solution to the problem was to employ the priority queue. It was to be implemented only in 2006. In the meantime, Gorzelańczyk and Murakowski were busy with their own science projects.
Gorzelańczyk used to attend a cybernetics conference in Cracow powered by my early inspiration: Prof. Ryszard Tadeusiewicz. For his presentation in 2005, Gorzelańczyk suggested we update our memory model. With the deluge of new data in molecular biology, a decade since the last formulation could make a world of difference. I thought that my ideas of finding a formula for building memory stability would make a good complement. This initial spark soon gained momentum in exchanges with Murakowski. Without those three brains working in concert and whipping up the excitement, the next obvious step would not have been made. Using the tools first employed in the model of intermittent learning in 1990, I decided to find out the function for stability increase. Once my computer started churning data, interesting titbits of information kept flowing serially. The job was to take just a few evenings. In the end, it took half the winter.
2013: Big picture re-awakening
Like in 2005, in 2013, the critical brain mass had to build up to push the new solutions through. However, I must give most credit to Biedalak. It was he who tipped the scales. With a never-ending battle for the recognition of SuperMemo‘s leadership and pioneering claims, he demanded we go on with the project and sent me for a short creative vacation to complete it. It was to be just one winter project, and it turned out to be two years, and it still consumes a lot of my time.
On Nov 09, 2014, we took a 26 km walk to discuss the new algorithm. Walktalking is our best form of brainstorming that always brings great fruits. Next day, we met in a swimming pool joined with Leszek Lewoc, worshipper of big data, who always has a great deal of fantastic ideas (I first met Lewoc in 1996, and his wife was probably a user as of SuperMemo as early as in 1992[verify!]). Simple conclusions from that brainstorming time were to use the two component model of memory to simplify the approach to the algorithm, simplify the terminology, and make it more human-friendly (no more A-Factors, U-Factors, R-Factors, etc.).
Increase in memory stability with rehearsal
To understand Algorithm SM-17, it is helpful to understand the calculations used to figure out the formula for the increase in memory stability. In 2005, our goal was to find the function of stability increase for any valid level of R and S: SInc= f(R,S). The goals and tools were pretty similar to those used in the quest to build the model of intermittent learning (1990).
Archive warning: Why use literal archives?
Until 2005, we were not able to formulate a universal formula that would link a repetition with an increase in memory stability. Repetition spacing algorithms were based on a general understanding of how stability increases when so-called optimum inter-repetition intervals are used (defined as intervals that produce a known recall rate that usually exceeds 90%). The term optimum interval is used for interval’s applicability in learning. The said repetition spacing algorithms also allow for determining an accurate stability increase function for optimum intervals in a matrix form. However, little has been known about the increase in stability for low retrievability levels (i.e. when intervals are not optimum). With data collected with the help of SuperMemo, we can now attempt to fill in this gap. Although SuperMemo has been designed to apply the optimum intervals in learning, in real-life situations, users are often forced to delay repetitions for various reasons (such as holiday, illness, etc.). This provides for a substantial dose of repetitions with lower retrievability in nearly every body of learning material. In addition, in 2002, SuperMemo introduced the concept of a mid-interval repetition that makes it possible to shorten inter-repetition intervals. Although the proportion of mid-interval repetitions in any body of data is very small, for sufficiently large data samples, the number of repetition cases with very low and very high retrievability should make it possible to generalize the finding on the increase in memory stability from the retrievability of 0.9 to the full retrievability range.
To optimally build memory stability through learning, we need to know the function of optimum intervals, or, alternatively, the function of stability increase ( SInc). These functions take three arguments: memory stability (S), memory retrievability (R) and difficulty of knowledge (D). Traditionally, SuperMemo has always focused on the dimensions S and D, as keeping retrievability high is the chief criterion of the optimization procedure used in computing inter-repetition intervals. The focus on S and D was dictated by practical applications of the stability increase function. In the presented article, we focus on S and R as we attempt to eliminate the D dimension by analyzing “pure knowledge”, i.e. non-composite memory traces that characterize knowledge that is easy to learn. Eliminating the D dimension makes our theoretical divagations easier, and the conclusions can later be extended to composite memory traces and knowledge considered difficult to learn. In other words, as we move from practice to theory, we shift our interest from the (S,D) pair to the (S,R) pair. In line with this reasoning, all data sets investigated have been filtered for item difficulty. At the same time, we looked for possibly largest sets in which representation of items with low retrievability would be large enough as a result of delays in rehearsal (in violation of the optimum spacing of repetitions).We have developed a two-step procedure that was used to propose a symbolic formula for the increase in stability for different retrievability levels in data sets characterized by low and uniform difficulty (so-called well-formulated knowledge data sets that are easy to retain in memory). Well-formulated and uniform learning material makes it easy to distill a pure process of long-term memory consolidation through rehearsal. As discussed elsewhere in this article, ill-formulated knowledge results in superposition of independent consolidation processes and is unsuitable for the presented analysis.
Two-step computation
In SuperMemo 17, it is possible to run through the full record of repetition history to collect stability increase data. This makes it possible to plot a graphic representation of the SInc[] matrix. That matrix may then be used in an effort to find a symbolic approximation of the function of stability increase. The same reasoning was used in 2005. The procedure was much simpler though. This can then be used to better understand Algorithm SM-17:
Archive warning: Why use literal archives?
The two-step procedure for determining the function of the increase in memory stability SInc:
- Step 1: Using a matrix representation of SInc and an iterative procedure to minimize the deviation Dev between the grades in a real learning process (data) and the grades predicted by SInc. Dev is defined as a sum of R-Pass over a sequence of repetitions of a given piece of knowledge, where R is retrievability and Pass is 1 for passing grades and 0 for failing grades
- Step 2: Using a hill-climbing algorithm to solve a least-square problem to evaluate symbolic candidates for SInc that provide the best fit to the matrix SInc derived in Step 1
Computing stability increase
The matrix of stability increase ( SInc[]) was computed in Step 1. In 2005, we could take any initial hypothetical plausible value of SInc. Today, as we know the approximate nature of the function, we can speed up the process and make it non-iterative (see Algorithm SM-17).
Archive warning: Why use literal archives?
Let us define a procedure for computing stability of memory for a given rehearsal pattern. This procedure can be used to compute stability on the basis of known grades scored in learning (practical variant) and to compute stability on the basis of repetition timing only (theoretical variant). The only difference between the two is that the practical variant allows of the correction of stability as a result of stochastic forgetting reflected by failing grades.
In the following passages we will use the following notation:
- S(t) – memory stability at time t
- S[r] – memory stability after the r th repetition (e.g. with S[1] standing for memory stability after learning a new piece of knowledge)
- R(S,t) – memory retrievability for stability S and time t (we know that R=exp -k*t/S and that k=ln(10/9))
- SInc(R,S) – increase in stability as a result of a rehearsal for retrievability R and stability S such that SInc(R(S,t),S(t))=S(t )/S(t’)=S[r]/S[r-1] (where: t’ and t stand for the time of rehearsal as taken before and after memory consolidation with t -t’ being indistinguishable from zero)
Our goal is to find the function of stability increase for any valid level of R and S: SInc= f(R,S).
If we take any plausible initial value of SInc(R,S), and use S[1]=S 1, where S 1 is the stability derived from the memory decay function after the first-contact review (for optimum inter-repetition interval), then for each repetition history we can compute S using the following iteration:
r:=1;
S[r]:=S1
repeat
t:=Interval[r]; // where: Interval[r] is taken from a learning process (practical variant) or from the investigated review pattern (theoretical variant)
Pass:=(Grade[r]>=3); // where: Grade[r] is the grade after the r-th interval (practical variant) or 4 (theoretical variant)
R:=Ret(S[r],t);
if Pass then
S[r+1]:=S[r]*SInc[R,S[r]]
r:=r+1;
else begin
r:=1;
S[r]:=S1;
end;
until (r is the last repetition)
In Algorithm SM-8, we can use the first-interval graph to determine S 1, which is progressively shorter after each failing grade.
We start the iterative process with a hypothetical initial value of matrix SInc[R,S], e.g. with all entries arbitrarily set to E-Factor as in Algorithm SM-2.
We can then keep using the above procedure on the existing repetition history data to compute a new value of SInc[R,S] that provides a lesser deviation from grades scored in the actual learning process (we use differences R-Pass for the purpose).
Incremental improvements are possible if we observe that:
Archive warning: Why use literal archives?
- if Pass=true and S[r]<Interval[r] then SInc[R,S[r-1]] entry is underestimated (and can be corrected towards Interval[r]/S[r]* SInc[R,S[r-1]])
- if Pass=false and S[r]>Interval[r] then SInc[R,S[r-1]] entry is overestimated
We can iterate over SInc[] to bring its value closer and closer to the alignment with grades scored in the learning process.This approach makes it possible to arrive at the same final SInc[R,S] independent of the original value of SInc[R,S] set at initialization
In Algorithm SM-17, instead of the above bang-bang incremental approach, we use actual forgetting curves to provide a better estimate of retrievability, which can then be used to correct the estimated stability. The ultimate stability estimate combines the theoretical prediction of retrievability, actual recall taken from forgetting curves (weighted for the availability of data), and the actual grade combined with the interval as in the above reasoning. By combining those three sources of information, Algorithm SM-17 can provide stability/interval estimates without the need to iterate over the SInc[] matrix over and over again.
Symbolic formula for stability increase
After many iterations, we obtain a value of SInc that minimizes the error. The procedure is convergent. With the matrix of stability increase available, we can look for a symbolic formula expressing the increase in stability.
Dependence of stability increase on S
Predictably, SInc decreases with an increase in S :
Archive warning: Why use literal archives?
In Step 2, we will use the SInc[R,S] matrix obtained here to obtain a symbolic formula for SInc.
Step 2 – Finding SInc as a symbolic formula
We can now use any gradient descent algorithm to evaluate symbolic candidates for SInc that provide the best fit to the matrix SInc derived above.
When inspecting the SInc matrix, we immediately see that SInc as a function of S for constant R is excellently described with a negative power function as in the exemplary data set below:
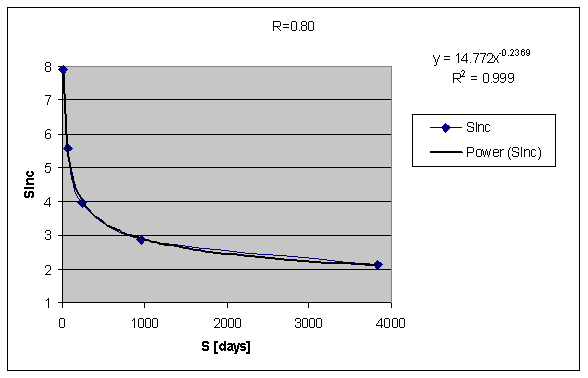
Which is even more clear in the log-log version of the same graph:
The conclusion on the power dependence between SInc and S above confirms the previous findings. In particular, the decline of R-Factors along repetition categories in SuperMemo has always been best approximated with a power function
Dependence of stability increase on R
As predicted by the spacing effect, SInc is greater for lower levels of R . Note, however, that the procedure used in 2005 might have introduced an artifact: the survival of a memory trace over time would linearly contribute to the new stability estimate. This is problematic due to the stochastic nature of forgetting. Longer survival of memories may then be a matter of chance. In Algorithm SM-17, more evidence is used to estimate stability, and the survival interval is weighed up with all other pieces of evidence.
Archive warning: Why use literal archives?
When we look for the function reflecting the relationship of SInc and R for constant S, we see more noise in data due to the fact that SuperMemo provides far fewer hits at low R (its algorithm usually attempts to achieve R>0.9). Nevertheless, upon inspecting multiple data sets we have concluded that, somewhat surprisingly, SInc increases exponentially when R decreases (see later to show how this increase results in a nearly linear relationship between SInc and time). The magnitude of that increase is higher than expected, and should provide further evidence of the power of the spacing effect. That conclusion should have a major impact on learning strategies.
Here is an exemplary data set of SInc as a function of R for constant S. We can see that SInc=f(R) can be quite well approximated with a negative exponential function:
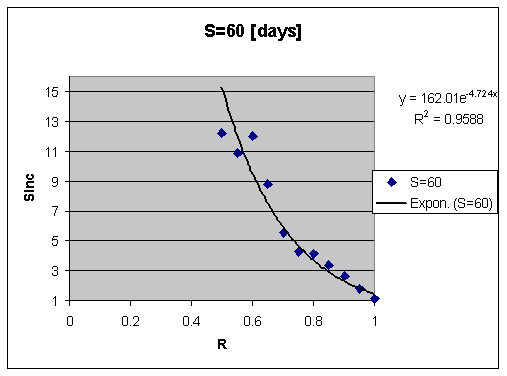
And the semi-log version of the same graph with a linear approximation trendline intercept set at 1:
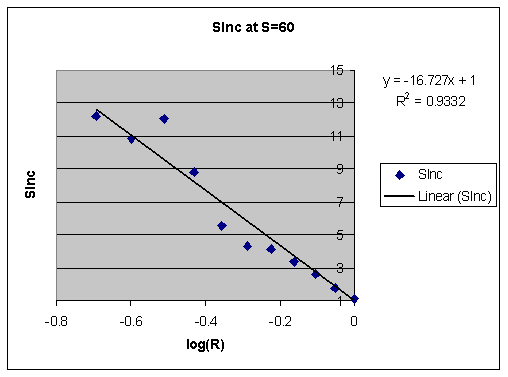
Interestingly, stability increase for retrievability of 100% may be less than 1. Some molecular research indicates increased lability of memories at review time. This is one more piece of evidence that repetitive cramming can hurt you not only by costing you extra time.
Dependence of stability increase on retrievability (2018)
Despite all the algorithmic differences and artifacts, the dependence of stability increase on retrievability for well-formulated knowledge is almost identical with that derived from data produced 13 years later by Algorithm SM-17.
Recall that in SuperMemo, we use forgetting curves to provide a better estimate of retrievability. This is then used to correct the estimated stability. By combining several sources of information, Algorithm SM-17 can provide more accurate stability estimates. There is still the old artifact of the survival of a memory trace that would linearly contribute to the new stability. This artifact can be weighed out parametrically. However, each time SuperMemo tries to do that, its performance metrics drop.
Despite all the improvements, and much larger data sets (esp. for low R), the dependence of stability increase on retrievability for easy items seems set in stone.
This perfect picture collapses when we add difficult knowledge into the mix. This is partly due to reducing the long survival artifact mentioned above. For that reason, new SuperMemos do not rely on this seemingly well-confirmed memory formula:
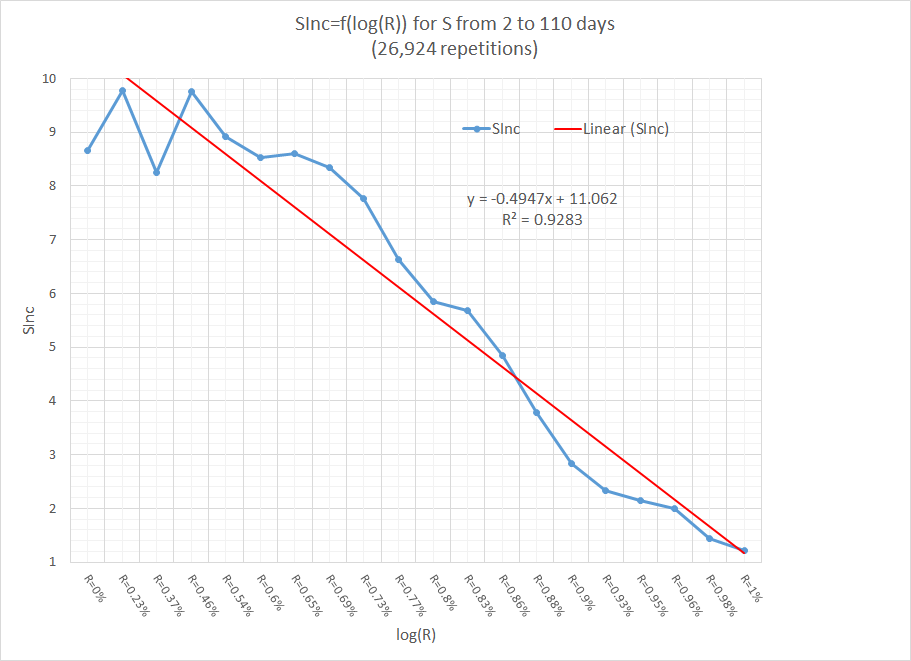
Figure: The strength of long-term memory depends on the timing of review. For well-formulated knowledge, long delays in review produce large increase in memory stability. Optimum review should balance that increase with the probability of forgetting. In the presented graph, the relationship between stability increase and the logarithm of retrievability (log(R)) is linear. Log(R) expresses time. Nearly 27,000 repetitions have been used to plot this graph. Observed memory stability before review spanned from 2 days to 110 days. Maximum increase in stability of nearly 10-fold was observed for lowest levels of retrievability. The stability increase matrix was generated with Algorithm SM-17 in SuperMemo 17
Memory stability increase formula
With the matrix of stability increase at hand, we could look for a symbolic expression of stability increase. The equation that has been found in 2005 will later be referred to as Eqn. SInc2005. Note that formulas used in Algorithm SM-17 differ:
Archive warning: Why use literal archives?
For constant knowledge difficulty, we applied two-dimensional surface-fitting to obtain the symbolic formula for SInc. We have used a modified Levenberg-Marquardt algorithm with a number of possible symbolic function candidates that might accurately describe SInc as a function of S and R. The algorithm has been enhanced with a persistent random-restart loop to ensure that the global maxima be found. We have obtained the best results with the following formula (Eqn. SInc2005):
SInc= aS -b *e cR+ d
where:
- SInc – increase in memory stability as a result of a successful repetition (quotient of stability S before and after the repetition)
- R – retrievability of memory at the moment of repetition expressed as the probability of recall in percent
- S – stability of memory before the repetition expressed as an interval generating R=0.9
- a, b, c, d – parameters that may differ slightly for different data sets
- e – base of the natural logarithm
The parameters a, b, c, d would vary slightly for different data sets, and this might reflect user-knowledge interaction variability (i.e. different sets of learning material presented to different users may result in a different distribution of difficulty as well as with different grading criteria that may all affect the ultimate measurement).For illustration, an average value of a, b, c, d taken from several data sets has been found to be: a=76, b=0.023, c=-0.031, d:=-2, with c varying little from set to set, and with a and d showing relatively higher variance. See the example: How to use the formula for computing memory stability?
Conclusions derived from stability increase formula
The above formula for stability increase differs slightly from later findings. For example, it seems to underestimate the decline in stability increase with S (low b). However, it can be used to derive a great deal of interesting conclusions.
Linear increase in value of review over time
Due to the spacing effect the potential for an increase in memory stability keeps growing over time in nearly linear fashion:
Archive warning: Why use literal archives?
The above formula produced SInc values that differed on average by 15% from those obtained from data in the form of the SInc matrix on homogeneous data sets (i.e. repetition history sets selected for: a single student, single type of knowledge, low difficulty, and a small range of A-Factors).
As inter-repetition interval increases, despite double exponentiation over time, SInc increases along a nearly-linear sigmoid curve (both negative exponentiation operations canceling each other):
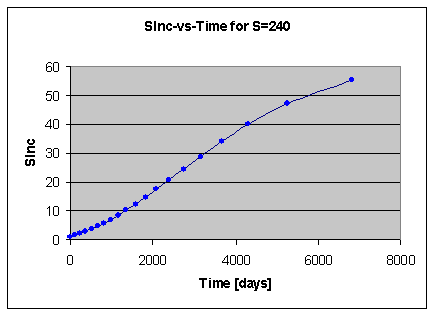
Figure: The graph of changes of SInc in time. This graph was generated for S=240 using Eqn. SInc2005.
The nearly linear dependence of SInc on time is reflected in SuperMemo by computing the new optimum interval by multiplying O-Factor by the actually used inter-repetition interval, not by the previously computed optimum interval (in SuperMemo, O-Factors are entries of a two-dimensional matrix OF[S,D] that represent SInc for R=0.9).
Expected increase in memory stability
Optimization of learning may use various criteria. We may optimize for a specific recall level or for maximization of the increase in memory stability. In both cases, it is helpful to understand the expected level of stability increase.
Let’s define the expected value of the increase in memory stability as:
E( SInc)= SInc*R
where:
- R – retrievability
- SInc – increase in stability
- E( SInc) – expected probabilistic increase in stability (i.e. the increase defined by SInc and diminished by the possibility forgetting)
The formula for stability increase derived in 2005 produced a major surprise. We used to claim that the best speed of learning can be achieved with the forgetting index of 30-40%. Eqn SInc2005 seemed to indicate that very low retention can bring pretty good memory effects. Due to the scarcity of low-R data back in 2005, those conclusions need to be taken with caution:
Archive warning: Why use literal archives?
From Eqn SInc2005 we have E( SInc)=( aS -b *e cR+ d)*R. By finding the derivative d ESInc/dR, and equating it with zero, we can find retrievability that maximizes the expected increase in stability for various levels of stability:
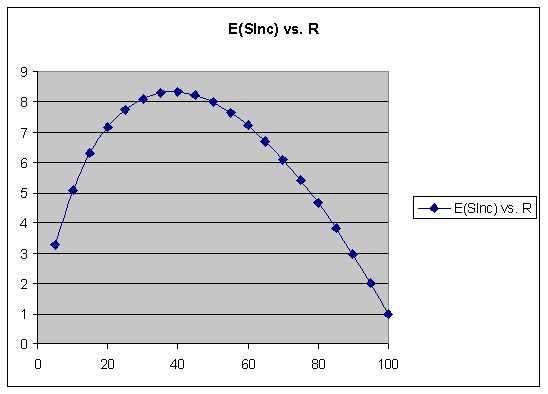
Figure: Expected increase in memory stability E(SInc) as a function of retrievability R for stability S derived from Eqn ( SInc2005). Using the terminology known to users of SuperMemo, the maximum expected increase in memory stability for short intervals occurs for the forgetting index equal to 60%! This also means that the maximum forgetting index allowed in SuperMemo (20%) results in the expected increase in stability that is nearly 80% less than the maximum possible (if we were only ready to sacrifice high retention levels).
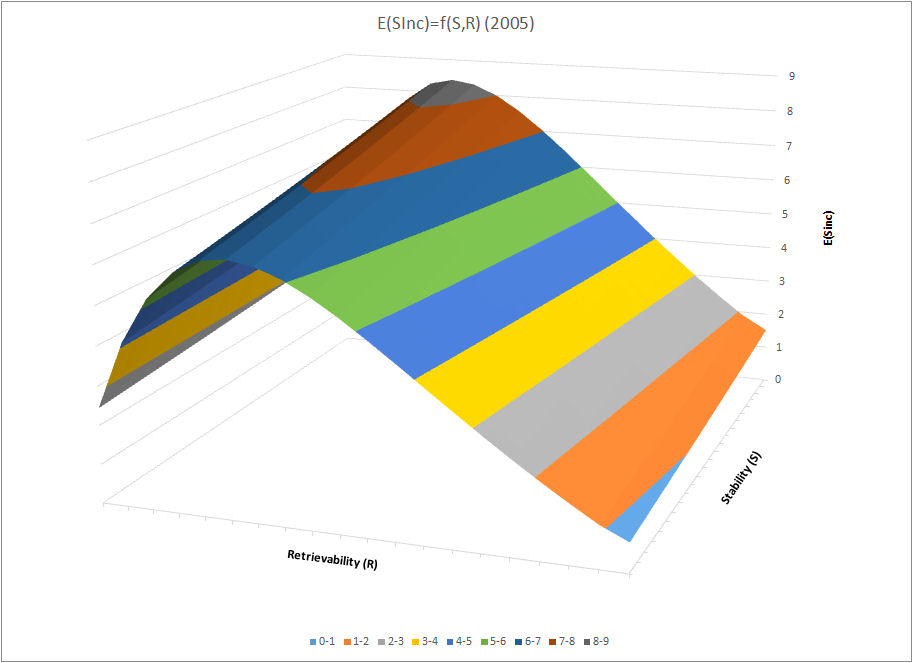
Figure: Expected increase in memory stability E(SInc) as a function of retrievability R and stability S as derived from Eqn SInc2005
Memory complexity in spaced repetition
Memory stability in spaced repetition depends on the quality of review which depends on memory complexity. As early as in 1984, I expressed that in my own learning in what later became known as minimum information principle. For effective review, knowledge needs to be simple. It may form a complex structure, but individual memories subject to review should be atomic. In 2005, we found a formula that governs the review of complex memories.
Georgios Zonnios was once an inquisitive teen user of SuperMemo. Today, he is an education innovator and a rich creative contributor to many of my ideas. He noticed:
Stability in the formula for stability of complex items is like resistance in an electronic circuit: many parallel resistors allow of leaks in current
Incidentally, in the early days of incremental reading, Zonnios independently arrived at the concept of incremental writing, which today may seem like an obvious step in employing the tools of incremental reading in creativity. This article has also been written by means of incremental writing.
This is how memories for complex items have been described and analyzed in 2005:
Archive warning: Why use literal archives?
The difficulty in learning is determined by complexity of remembered information. Complex knowledge results in two effects:
- increased interference with other pieces of information
- difficulty in uniform stimulation of memory trace sub-components at review time
Both components of difficulty can be counteracted with the application of appropriate representation of knowledge in the learning process.
Let us see how complexity of knowledge affects build up of memory stability.
Imagine we would like to learn the following: Marie Sklodowska-Curie was a sole winner of the 1911 Nobel Prize for Chemistry. We can take two approaches: one in which knowledge is kept complex, and one with easy formulations. In a complex variant, a double cloze might have been formulated for the purpose of learning the name of Marie Curie and the year in which she received the Nobel Prize.
Q: […] was a sole winner of the […] Nobel Prize for Chemistry
A: Marie Sklodowska-Curie, 1911
In a simple variant, this double cloze would be split and the Polish maiden name would be made optional and used to create a third cloze:
Q: […] was a sole winner of the 1911 Nobel Prize for Chemistry
A: Marie (Sklodowska-)CurieQ: Marie Sklodowska-Curie was a sole winner of the […](year) Nobel Prize for Chemistry
A: 1911Q: Marie […]-Curie was a sole winner of the 1911 Nobel Prize for Chemistry
A: Sklodowska
In addition, in the simple variant, a thorough approach to learning would require formulating yet two cloze deletions, as Marie Curie was also a winner of 1903 Nobel Prize for Physics (as well as other awards):
Q: Marie Sklodowska-Curie was a sole winner of the 1911 Nobel Prize for […]
A: ChemistryQ: Marie Sklodowska-Curie was a sole winner of the 1911 […]
A: Nobel Prize (for Chemistry)
Let us now consider the original composite double cloze. For the sake of the argument, let’s assume that remembering the year 1911 and the name Curie is equally difficult. The retrievability of the composite memory trace (i.e. the entire double cloze) will be a product of the retrievability for its subtraces. This comes from the general rule that memory traces, in most cases, are largely independent. Although forgetting one trace may increase the probability of forgetting the other, in a vast majority of cases, as proved by experience, separate and different questions pertaining to the same subject can carry an entirely independent learning process, in which recall and forgetting are entirely unpredictable. Let us see how treating probabilities of recall as independent events affects the stability of a composite memory trace:
(9.1) R=R a*R b
where:
- R – retrievability of a binary composite memory trace
- R a and R b – retrievability of two independent memory trace subcomponents (subtraces): a and b
(9.2) R=exp -kt/Sa*exp -kt/Sb=exp -kt/S
where:
- t – time
- k – ln(10/9)
- S – stability of the composite memory trace
- S a and S b – stabilities of memory subtraces a and b
(9.3) -kt/S=-kt/S a-kt/S b=-kt(1/S a+1/S b)
(9.4) S=S a*S b/(S a+S b)
We used the Eqn. (9.4) in further analysis of composite memory traces. We expected, that if initially, stability of memory subtraces S a and S b differed substantially, subsequent repetitions, optimized for maximizing S (i.e. with the criterion R=0.9) might worsen the stability of subcomponents due to sub-optimal timing of review. We showed this not to be the case. Substabilities tend to converge in the learning process!
Stability of complex memories can be derived from substabilities of atomic memories
Convergence of sub-stabilities for composite memory traces
It was easy to simulate the behavior of complex memories in spaced repetition. Their substabilities tend to converge. This leads to inefficient review and a slow buildup of stability. Today we can show that at a certain level of complexity, it is no longer possible to build memory stability for long-term retention. In short, there is no way to remember a book other than just re-reading it endlessly. This is a futile process.
Archive warning: Why use literal archives?
If we generate a double-cloze, we are not really sure if a single repetition generates a uniform activation of both memory circuits responsible for storing the two distinct pieces of knowledge. Let us assume that the first repetition is the only differentiating factor for the two memory traces, and that the rest of the learning process proceeds along the formulas presented above.
To investigate the behavior of stability of memory subtraces under a rehearsal pattern optimized for composite stability with the criterion R=0.9, let us take the following:
- S a=1
- S b=30
- S=S a*S b/(S a+S b) (from Eqn. 9.4)
- SInc= aS -b *e cR+ d (from Eqn. SInc2005)
- composite memory trace is consolidated through rehearsal with R=0.9 so that both subtraces are equally well re-consolidated (i.e. the review of the composite trace is to result in no neglect of subtraces)
As can be seen in the following figure, memory stability for the composite trace will always be less than the stability for individual subtraces; however, the stabilities of subtraces converge.
Figure: Convergence of stability for memory sub-traces rehearsed with the same review pattern optimized for the entire composite memory trace (i.e. review occurs when the composite retrievability reaches 0.9). The horizontal axis represents the number of reviews, while the vertical axis shows the logarithm of stability. Blue and red lines correspond with the stability of two sub-traces which substantially differed in stability after the original learning. The black line corresponds with the composite stability (S=S a*S b/(S a+S b)). The disparity between S a and S b self-corrects if each review results in a uniform activation of the underlying synaptic structure.
Composite stability increase
Archive warning: Why use literal archives?
Let us now figure out how much SInc differs for composite stability S and for subtrace stabilities S a and S b? If we assume the identical stimulation of memory subtraces, and denote SInc a and SInc b as i, then for repetition number r, we have:
SInc a=SInc b= i
S a[r]=S a[r-1]* i
S b[r]=S b[r-1]* iS[r]=S a[r]*S b[r]/(S a[r]+S b[r])=
=S a[r-1]*S b[r-1]* i 2/(S a[r-1]* i+S b[r-1]* i)=
= i*(S a[r-1]*S b[r-1])/(S a[r-1]+S b[r-1)= i*S[r-1]
In other words:
(11.1) SInc= i=SInc a=SInc b
The above demonstrates that with the presented model, the increase in memory stability is independent of the complexity of knowledge assuming equal re-consolidation of memory subtraces.
Composite stability increase is the same as the increase in stability of sub-traces
2014: Algorithm SM-17
The newest SuperMemo algorithm in its design can be used to summarize its own phylogeny. It can also be used to write the counterfactual history of spaced repetition. If there were no dinosaurs, humans might not have emerged or might look differently. However, the entire dino branch of the evolutionary tree could easily be chopped off, and still keep humans safe on their own mammalian branch.
In a similar fashion, we can show a seemingly deterministic chain of linked events in the emergence of spaced repetition and Algorithm SM-17. This can be used to prove that Biedalak or Murakowski were more important for history of spaced repetition than Ebbinghaus. Anki was more important than Pimsleur. Gary Wolf provided more impact than William James.
However, the maximum impact of spaced repetition is yet to be seen and confluence of forces may re-arrange those early influences. In particular, with an explosion in legitimate competition, the central role of SuperMemo can only be retained with further innovation (e.g. see neural creativity).
Here is how I would explain the entire Algorithm SM-17 using the building blocks of history as written for this article:
- the key to long-term retention is to compute optimum spacing (1985)
- as spacing depends on memory complexity, we need to begin with classifying items into difficulty categories (1987)
- we find the optimum review time by plotting the forgetting curve, which indicates a moment when retention drops below an acceptable level (1991)
- to find optimum time in scarce data, we need to use approximations, and it helps to know that forgetting is exponential (1994)
- as the speed of forgetting depends on memory stability, the whole algorithm must be designed with two component of memory at its core (1988). The lack of consideration for the model may be the chief mistake made by developers of competitive spaced repetition algorithms, e.g. as in the case of neural network approach (1997)
- the key power of the two components model is to make it possible to compute the increase in memory stability at review (2005)
- the algorithm must build the model of memory by collecting repetition data. It must be adaptable to the available information (1989)
- before data is available, it is helpful to start with a universal memory formula (1990)
- further minor adjustments and improvements can make a world of difference (1995), e.g. post-lapse interval, absolute difficulty, fast multi-dimensional regression, etc.
And so, step by step, Algorithm SM-17 has emerged at the top of the evolutionary tree in spaced repetition.
Exponential adoption of spaced repetition
Slow start of Algorithm SM-2
Algorithm SM-2 was first used in learning on Dec 13, 1987 and with minor tweaks survived to this day in a number of applications. SuperMemo abandoned the algorithm in 1989, however, it keeps popping up in new applications with a frequency that must be approaching a few new developments each month. I lost count long ago. Some of the mutations contradict the principles of SuperMemo and still take on its label. Most often, the violations include intervals measured in minutes, or halving intervals at fail grade (Leitner style). Those mutations also lead to some fake news about SuperMemo. Note that fake news was one of the greatest incentives for writing this article.
When Duolingo speaks in their paper of hand-picked parameters in reference to SuperMemo, it must be a result of relying on some older texts, perhaps second-hand texts, perhaps texts written in reference to Algorithm SM-2. After all, SuperMemo was pretty adaptable as of 1989 and Algorithm SM-17 is the most adaptable specimen in existence.
Some of the blame for misinformation is mine as I stopped caring about peer review, and let the information wild on the web with insufficient mythbusting effort.
The first applications to use Algorithm SM-2 were non-commercial offshoots of SuperMemo for Atari in the 1980s. Later, minor clones of SuperMemo (e.g. for handheld computers) opted for variants of Algorithm SM-2 with various own innovations, of which many provided painful lessons on the impact of disrespect of memory in the name of cramming.
By 2001, SuperMemo World moved ahead by five major generations of the algorithm. All major software lines, incl. on-line SuperMemo and SuperMemo for Windows adopted the data driven variants of the algorithm. supermemo.net became one of the pioneering e-learning platforms (today evolving into supermemo.com ). SuperMemo for Windows pioneered self-learning solutions such as incremental reading or neural creativity. In the meantime, Algorithm SM-2 became an easy first-choice option for other developers.
1998: publishing and acceleration
On May 10, 1998, Algorithm SM-2 was opened to the public and published on the web here.
Mnemosyne was first to pick the tool as the offshoot of neural network MemAid created in 2003. As of 2006, Mnemosyne keeps collecting repetition history data running a mutation of Algorithm SM-2. As a free multi-platform application, Mnemosyne quickly reached a large base of users, e.g. on Linux, or those users who have Latex requirements.
Anki was born on Oct 6, 2006. It was based on Algorithm SM-2 and for nearly a decade provided the widest reach for the algorithm. It is still going strong. Anki introduced a great deal of innovations into their algorithm but refused to advance beyond its basic principles (see: criticism of SM3+).
In 2007, when we met Gary Wolf, SuperMemo looked like a sad deserted island that begged a question: if it is so good, why others don’t try to copy the algorithm. Anki and Mnemosyne were little known at that time. Wolf’s article in Wired in 2008 caused a nice rush for education software developers to implement a form of spaced repetition. Algorithm SM-2 seems like a low fruit to pick and its expansion accelerated. Many users of SuperMemo claim they would never find the program without Wolf’s article in Wired. Krzysztof Biedalak likes to joke though that Wolf’s article was indeed a breakthrough. However, not for SuperMemo. It simply opened the floodgates for the competition to rush in into the field of spaced repetition.
2008: explosion
Quizlet was written in 2005 and released in 2007. It was initially a typical cramming tool, however, by 2015, backed by venture capital, Quizlet announced a higher emphasis on long-term retention, which resulted in adopting a variant of Algorithm SM-2. By 2017, they decided to use machine learning to deploy a new algorithm that would capitalize on billions of repetition records collected. The short stint for SuperMemo at Quizlet must have given a mutation of Algorithm SM-2 an exposure to the largest user base ever. At the time, Quizlet reported reaching every second high school student in the US.
The new approach taken by Quizlet is based on a strong foundation, and can lead to a very strong tool, however, this is very disappointing to hear the motivation behind the move towards better algorithms: ” Cramming is a reality for many students, and we want to help them make the best of their study time however they spend it“. Algorithm SM-17 provides for more freedom to students: (1) to advance learning when in need, or (2) to delay low priority material. However, we always discourage cramming as a bad practice. It is schools that need to adapt to human brain, not the other way around. This stubborn stance on learning efficiency hurts SuperMemo, but it will never change.
That move away from a simple review schedule by Quizlet in 2017 is probably the move past the peak of popularity for the old venerable algorithm. New competitors will need to go for intelligent tools, or perhaps for licensing Algorithm SM-17. The news is good.
How many people use spaced repetition?
In mid-1991, one of my classmates tried to cheer me up. He predicted we will be successful and we will manage to sell 10-20 copies of SuperMemo. I was more optimistic. In 1993, I predicted 1 million users by 1996. In 1994, Enter, Poland, mentioned similar optimism of Marczello Georgiew:
In questionnaires received at SuperMemo World, when asked what they like most in the program, users of SuperMemo overwhelmingly indicate its effectiveness. The software may be OK, but what really counts is results in learning. How about dislikes? Users are not pleased with this or that, most often with the fact that, even in Poland, SuperMemo is always released first in English. But there is no particular turn-off that takes precedence. Definitely, nobody questions the fact that with SuperMemo one can learn faster and never to worry about forgetting. Taking this rosy picture into heart, one might wonder why has SuperMemo not yet sold in millions of copies worldwide. Marczello Georgiew, Marketing Director at SuperMemo World proposed to recall the problems Graham Bell experienced when trying to introduce his funny machine for talking over a wire or how pessimistic the predictions of industry futurologists were about the expansion of the air-polluting mechanical horse. Then he adds confidently: It took Wozniak 10 years to turn necessity into invention, give us half this time, and we will turn his invention into a global necessity.
In my 1 million users prediction, I was off by 3 years, and had to make a distinction between short-timers and active users. The proportion of active users of spaced repetition kept dropping with wider adoption. In 2007, we estimated the reach of SuperMemo to be 5 million, of which most were freeware and partwork users. Of those 5 million, only 0.4-4.0% were active users. This might have been as few as 20,000 students.
In 2009, Gwern Branwen estimated the population of active users to be around 100,000, which seems to agree with my numbers. This does not sound too optimistic for two decades of hard work at SuperMemo World.
Let’s then have a closer look at the reach of spaced repetition today. My estimates below met with a great deal of skepticism. I agree that they are based on a great deal of guesswork. However, once you are on an exponential curve of growth, even large estimate errors make little difference. You can overestimate by 200% and still catch up quickly in no time.
This is why I do not hesitate to say that the exponential growth in the adoption of spaced repetition streaks towards the big B: one billion users. Amazon’s Kindle has added spaced repetition to its Flashcard option in Vocabulary Builder. Even users of SuperMemo who use Kindle may know nothing of the fact. Flashcards with books is the general idea that was to bring SuperMemo to NASDAQ back in 1996 if we succeeded in persuading venture capital that the idea made sense.
However, to hit a billion users we need another breakthrough. The first obvious candidate that comes to mind is Facebook, which might wire spaced repetition into the cacophony of social interaction, and make free learning transparent, i.e. where users learn without ever showing intent.
If you think Facebook and spaced repetition are incompatible worlds, consider the world of advertising. These days we all hate advertising. No matter how well it is targeted. However, the pestering party can maximize the memory effect and minimize the annoyance (i.e. retrievability) by employing spaced repetition. Even the most captivating TV advert will get on your nerves by the third exposure. Spaced review could ensure that retrievability is low and retention high.
Last but not least, spaced review may be taken on by the bad guys. The makers of fake news and worse. A publicity charlatan might pull strings behind the back of a world leader. He may shake the world in spaces. This may expose the whole world to spaced repetition to be sure we all remember.
The top of the pyramid is so bad that I will not even list it. I don’t want to give bad guys any ideas.
My estimates below include a couple of points that are pretty certain. The first user in 1985, second in 1987, one million by 2000, and my laborious estimate of 5 million in 2007. Today, Duolingo claims 200,000 users. Quizlet claims even more. The growth is still showing few sign of saturation.
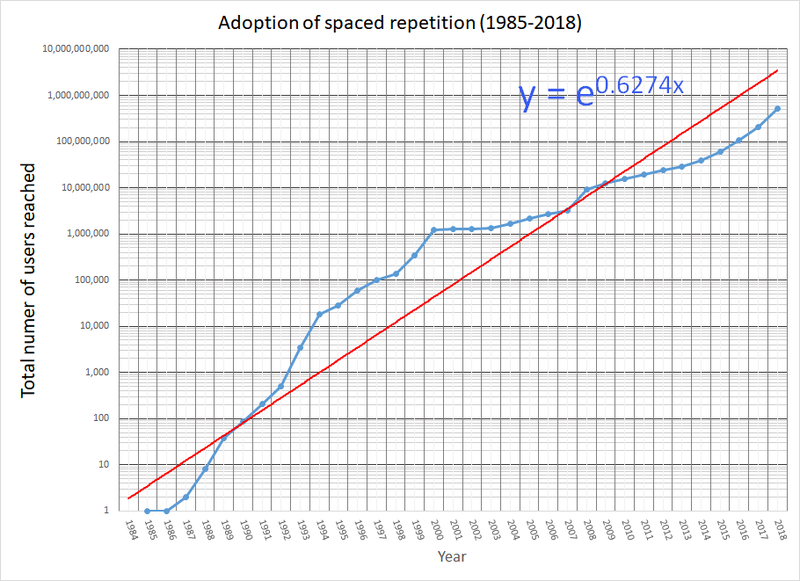
Figure: We expected spaced repetition to show signs of saturation long ago. However, through transmutation, it will inevitably hit a billion users at some point. Once it becomes integrated with human digital life, it will affect nearly everyone. If my estimate is right, the speed of adoption, aided by the web, is still ahead of the telephone, car, and the radio. We never thought it was possible to compete with Pokemons or Angry Birds though. The exponential regression formula in the graph is: Reach=exp((year-1984)*0.63). The red line determined by that formula crosses 1 billion just about now
Today, with almost no barrier of entry, there are many students who try and drop out after weeks or even days of use. The proportion of active users may be very low. A billion users with negligible learning is still little learning. The next step in the job is to produce a cultural paradigm shift that will add value to efficient long-term learning. We need to begin with a change to the system of schooling and to adopt the principles of free learning.
Once spaced repetition hits a billion users, cultural paradigm shift will be necessary to convert usership to actual benefits in long-term quality learning
The road ahead is still very long.
Summary of memory research
Problem with spaced repetition research
History of research on spaced repetition has been plagued by the following factors:
- guesses and heuristics used in place of mathematical optimization
- poor interaction between theory and practice with science focused on simple experiments and practice focused on simple tools
- terminological inconsistency that leads to cycles of forgetting and re-discovery!
The above agrees with my ranking of factors of failure . Until the arrival of personal computing and the web, it was hard to escape the vicious cycle.
Spaced repetition intuitions
When we asked teenagers a set of questions about how their memory works, a large proportion could come with pretty good guesses about repetition spacing without ever making any measurements. In particular, they often correctly guess that the first optimum inter-repetition interval might be 1-7 days long and that successive intervals will increase. Moreover, many could guess that the second interval might be a month long and that successive intervals might double. In other words, spaced repetition is a common intuition.
Early memory research
In 1885, Hermann Ebbinghaus made a major contribution to the science of memory. He experimented on himself and came up with the first outline of the forgetting curve. He was also aware of the spacing effect. He never worked on spaced repetition. I do not credit Hermann for an inspiration in my work over spaced repetition as I simply had no idea who Hermann was and what he accomplished. I designed my own measurement that led to spaced repetition. In an unrelated and forgotten exercise, I also produced my own forgetting curve that might have influenced my thinking. Hermann’s curve was much steeper and might have actually discouraged further work (see: Error of Ebbinghaus forgetting curve). Our Adam Mickiewicz University library was well stocked up with “ancient” pre-WW2 German literature, however, I knew no German. Mine was an ignorant solo effort. I read about Ebbinghaus later, and mentioned his forgetting curve in my Master’s Thesis.
By 1901, in writings of William James, the superiority of spaced review seemed clear and it seemed like a matter of time before it permeates the learning theory with optimization of spacing taken as the next obvious step. It was not to be. For another 8 decades.
In his popular book of 1932, C.A. Mace has suggested a simple spaced repetition schedule: 1 day, 2 days, 4 days, 8 days, etc. Good guess! Mace’s effort was forgotten though because spaced repetition “on paper” before the era of the Internet must have hardly been appealing. For a good start, Mace would have to shine with a good example. I bet that was not easy. Herr Hitler dominated the news at that time.
1960s: The Renaissance
In 1966, Herbert Simon had a peek at Jost’s Law derived around 1897 from Ebbinghaus’s work. Simon noticed that exponential nature of forgetting necessitates the existence of a memory property that today we call memory stability. Simon wrote a short paper and moved on to hundreds of other projects he was busy with. His text was largely forgotten.
At roughly the same time, Robert Bjork had a great deal of innovative ideas in reference to learning and memory. As it often happens, he was ahead of his time. Teachers hardly ever listen to psychologists. Students do not even know their names. If Bjork was a programmer, we might have had the first popular application of spaced repetition a decade earlier. I think he would just not let a great idea off the hook. It was Bjork who seems to have been first to clearly separate retrieval strength and storage strength in a model analogous to our two component model of memory.
In 1967, Paul Pimsleur could clearly see that spaced repetition could be a great tool for learning word-pairs in language learning. Like SuperMemo, he struggled with terminology and used the term “graduated-interval recall”. In our “serrated forgetting curve” challenge, Pimsleur came closest with the earliest known serrated curves graph as in the picture:
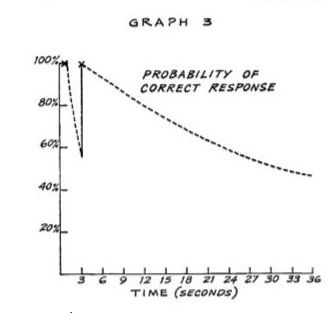
Perhaps we will discover earlier sketches of the idea, however, for technical reasons, the older the print, the less rich it is in graphs, which we today generate en masse in Excel.
Pimsleur’s intervals extended into periods of hours, minutes and even seconds. It was a reflection of an intuition, not measurement. He extended his reasoning from declarative knowledge that can easily be measured (e.g. word pairs) to procedural knowledge and audio-pattern recognition, as in learning pronunciation. SuperMemo solves this problem by separating word-pair learning from pronunciation, spelling, recognition, synonyms, and the like. As a result, e.g. in Advanced English, we never need to reduce intervals beyond user’s standard startup stability, which rarely drops down below a day. For practical reason and due to the role of sleep, SuperMemo never uses intervals shorter than 1 day. Sleep is also the main reason why the algorithm uses 1-day resolution in the length of intervals. SuperMemo makes it possible to review multiple times in a day, but this is part of a subset review that, on occasion, may appear useful (e.g. when cramming for an exam). Pimsleur’s interval recommendations were different than those of Mace or SuperMemo on paper ( Algorithm SM-0). They were not a result of a measurement, but a result of a speculation, which ranged from solid to poor. Pimsleur thought of ensuring recall of 60%, which is very low by SuperMemo standards. He bet on startup stability of 5 seconds, while SuperMemo uses 1-15 days, which is just fine for 90% recall of well-formulated knowledge. Pimsleur’s base of interval exponentiation ( E-Factor) was 5, which should be 1.4-2.5 in most cases. As a result, Pimsleur’s spacing differs dramatically from SuperMemo’s, and should not be used as a benchmark in algorithmic metric. In his original paper (1967), Pimsleur proposed intervals of 5 sec., 25 sec., 2 min., 10 min., 1 hour, 5 hours, 1 day, 5 days, 25 days, 4 months, and 2 years. The differences came mostly from the practise based on materials of different character (equivalent to high complexity in SuperMemo). The use of seconds, minutes and hours is tantamount to cramming and is strongly discouraged in SuperMemo. Instead, optimization of knowledge representation is advised.
In 1969, Alfred Maksymowicz wrote “Read and think”. You will not find his book in your library. It was written in Polish and for a narrow circle of students of technical universities. It mentioned spaced repetition, forgetting curves, and even how the forgetting index might determine the optimum interval. Maksymowicz proposed the first optimum interval to be 3 days. As many efforts before and after, this good advice remained largely ignored. Students rush to pass an exam and then forget. Cram and dump is a principle by which the pressure of schooling destroys the prospects of good long-term learning. I know of Maksymowicz’s book only because I studied at a technical university in Poland, and I was pretty loud of my own spaced repetition method. I can only imagine that there have been dozens other similar texts where intuitions were formulated as a good advice that then remained ignored by the masses. Without the coincidence of time and space, future texts on spaced repetition might never notice Maksymowicz ever existed. Maksymowicz might have been inspired by Pimsleur, Mace, his own intuition, or other potential texts of which I have no knowledge. Maksymowicz gives credence to the words of Szafraniec, skeptical of SuperMemo: “all has occurred before”.
1972: Leitner box
The greatest practical and algorithmic success in the area of spaced review before SuperMemo can be attributed to Sebastian Leitner. In 1972, he proposed the Leitner box system . In a Leitner system, flashcards are prioritized and dumped to boxes corresponding with different stability levels. The Leitner system has one huge advantage over the theoretical advice dished prior to his proposition: it was practical. It was a system anyone could use with little introduction. Even SuperMemo on paper ( 1985) seems complex in comparison.

Figure: An incorrect mutation of the Leitner system where failed answers are moved back by one box only (source: Wikipedia). This variant was in use in Duolingo for a while
The Leitner box is not a spaced repetition tool. It is a prioritization tool. There is no concept of an interval, let alone optimum interval. The name box comes from the original implementation in the form of physical flashcard boxes with not association to passing time. When the Leitner box is used regularly on a small-sized collection of flashcards, it simulates the behavior of spaced repetition. If intervals are too short, it leads to cramming. If they get too long, it leads to sub-optimum outcomes. However, in SuperMemo, low priority material may also be postponed cyclically and yield very long intervals which reduce expected stability increase, but carry a larger stability increase for items that survive longer intervals. In the 1990s and early in the new millennium, the Leitner system was used in many successful flashcard applications. As they kept tinkering and improving the review procedures, these apps might have actually evolved into a full-blown spaced repetition system. Their application declined though due to the popularity of SuperMemo’s Algorithm SM-2 that turned out to be easy to implement and vastly superior.
Newer software mutations of the Leitner box system may attach intervals to priority boxes, e.g. 16 days for Box #5, but this approach has flaws tantamount to cramming: (1) failure still leads to the regression of intervals, while it should lead to resumed learning, (2) five repetitions in the first month does not compare well to well-formulated knowledge that may reduce the cost of learning in SuperMemo in the first month alone by 60-80%, and (3) more boxes would be needed. We have seen intervals well beyond maximum human lifespan in SuperMemo. The needs for lifetime applications are 200 thousand percent higher. This is the difference between a permastore interval and 16 days. 11 extra boxes would be needed to cover the lifetime at E-factor of 2.
Today, one of the most popular systems for learning languages is Duolingo. For a long while, it used the Leitner system. Today they employ their own new algorithm based on retrievability predictions. However, they still used the Leitner system as a benchmark. To make matters worse, their benchmark used the reverse transfer of flashcard in priority boxes (where the post-lapse stability is overestimated). Normalized Leitner might be used as a benchmark, however, simple normalization equivalent to using E-factor of 2, may produce different results than the choice of E-factor 1.6. In the future, all algorithms should switch to a universal metric proposed by SuperMemo, and Algorithm SM-2 might become a useful metric benchmark that can be implemented in parallel with proprietary solutions. I hope users will demand clarity, statistics, metrics, and full openness in that respect.
In the 1970s, Tony Buzan would focus on structured knowledge with his mind-mapping innovations. Mind maps and SuperMemo would, paradoxically, stand in conflict due to a lack of a good unifying theory. In short, we need good models to understand the world, and we need the spaced review to retain the components of the model in the long term. Buzan also had his own ideas how the review should be spaced. When he first met SuperMemo in the early 1990s, he instantly agreed with the concept, however, he always preferred to focus on knowledge structure rather than a mere review.
1980s: SuperMemo
My own work entered the picture in 1982 when I really got fed up with a never-ending process of forgetting. I wanted to learn biochemistry and physiology. I would read books, make notes and it would all be for nothing due to the process of forgetting. Even the most important facts could slip the memory at the most unfortunate moment (e.g. exam). I decided to employ active recall. Instead of just making notes, I would make notes as questions and answers. I could cover answers and respond using active recall. This would dramatically improve learning. This is how it is done in SuperMemo to this day. This new approach had a lovely impact on boosting my love of learning.
By 1984, I was fluent enough with my active recall approach to know that complex questions don’t work. If you pack too much stuff into the answer, e.g. make a long list of it, you will keep forgetting. This would be futile learning. I later called that quest for simplicity ” minimum information principle“. Today, this principle is one of the first mentioned among 20 rules of knowledge formulation.
The real breakthrough came in 1985, i.e. exactly 100 years after the publication of Ebbinghaus’ dissertation on memory. I wanted to check how the spacing of review affects recall. I needed to figure out the length of optimum intervals between repetitions. Obviously, those intervals exist. I only needed to measure them. The experiment is described here. The experiment was simple, rough, lazy, and hurried. Instead of taking a patient few years to find out all details, after 6 months I formulated the first SuperMemo algorithm. You can call it the first case of somewhat scientific spaced repetition. My research was based on one person, and one type of learning material, but it was universal enough to have many faithful users years later. On Jul 31, 1985, I started learning biochemistry using the new method. This is the birthday of computational spaced repetition. The computer program SuperMemo for DOS came in 1987, and the name SuperMemo in 1988.
In the 1980s, Jaap Murre’s Memory Chain Model was one of the early models of memory that might have led to a solid spaced repetition algorithm. It even had its own early application, Captain Mnemo, that might have competed with SuperMemo for priority in the field. Captain Mnemo and OptLearn are examples of why, in academic environments, great theories are often not followed by practical implementations that could gain wider appeal.
In 1991, SuperMemo World was formed and its beginnings are described here. By 1999, we started using the term “spaced repetition” instead of the “SuperMemo method”. For recent developments at SuperMemo World see here.
The anatomy of failure and success
Formula for research failure
Some intuitions about spaced repetition are pretty common. This gives rise to a major question: why has not spaced repetition been investigated earlier and why didn’t it permeate into the practice of learning? Intuitions are not enough, a good experimental design is also vital. This section explains why others were close but failed. How Ebbinghaus or Spitzer might have brought spaced repetition to life 90-130 years earlier. There must be something wrong with the immediacy of gratification in peer review and battle for grants. Why is there so much buzz in the field of drugging kids for school, while diseases that take a heavy death toll in less developed countries get little interest?
In this chapter, I try to figure out why spaced repetition was so late to come. Here is my take prioritized by the impact factor:
- computers make a dramatic difference in learning efficiency in spaced repetition, early formulations would not be viral enough even in the era of the Internet
- web perpetuates knowledge and crystallizes its essence (e.g. at Wikipedia)
- intuitions do not ensure good experimental design. Myself, Ebbinghaus, Spitzer, and others, produced designs that would add more noise and complexity to the issue
- human culture is in a perpetual flow. We massively forget and re-discover old findings. This is as true of individuals as it is of cultures. Science is also subject to fads, fashions and forgetting. Only now, spaced repetition has reached the “impact density” needed to become “common knowledge”. See: Discontinuity in the research on spacing effect
- self-interest and self-learning are best drivers of applicability. Science permeates lives via practical applications. SuperMemo was the first practical application of spaced repetition that could reach thousands and then millions of users
- there used to be a great deal of confusion between short and long-term memory, between spacing in lists, and spacing in a single day, and even between procedural and declarative learning
- expanding, contracting or equally spaced schedule can all be made superior given appropriate timing
- experimenters tend to use heterogeneous material (poems, lists, nonsense syllables, pages of questions, groups of students, etc.)
- experiments where passive review is used instead of active recall do not benefit from the testing effect
- experiments where intervals are measured in intervening items are based on different memory mechanisms and should not even be labelled as spaced repetition. To this day, a lot of confusion in research is caused by mixing up the measures of intervals without a clear separation of terminology
- short-span of research projects makes spaced repetition investigations hardly possible
- focus on classroom applications has confused the outcomes. Schools are not a good place for learning. Research that optimizes for school environment is of little relevance in free learning
- ages old distinction between learning and retention confuses the thinking about optimal education. The distinction comes from schooling in which we learn first and then pray to forget little
- terminology keeps mutating and this makes hard for new generations of researchers to capitalize on prior work. Even our own 1994 paper uses the term repetition spacing. For the list of terminological mutations see this Glossary entry. Web, wisdom of the crowds, and wikis (like this one) are likely to remedy the problem of terminology
In 2006, Will Thalheimer produced an excellent research review of spaced repetition research. It was based on over 100 research articles. However, in the summary Thalheimer cast doubt about the value of progressive spacing. This shows that even dozens of papers won’t help if the experimental design is based on incorrect models.
In spaced repetition, it is not enough for review to be expanding. The review needs to be optimally expanding
Failed experimentation
I will list three cases of experiments that were bound to fail or to confuse:
- Herman Ebbinghaus (1885) was motivated by the science of memory. His intuitions were excellent, however, in the name of purity, he focused on nonsensical syllables. Inadvertently, he contributed to complexity of memory and interference, which he aimed to avoid. His forgetting curve is ruthless and discouraging. Had Ebbinghaus learned meaningful material of interest, he might have had extended the scope of his experiment. We all know from school that cramming nonsense is a form of mental torture. Had Ebbinghaus opted for practical applications, like myself, we might have had a paper variant of spaced repetition born a neat 100 years before the fact. Naturally, without computers, without the web, his ideas might still fall into the pit of silence for a century, as much as it has actually happened to the concept of the spacing effect.
- Herbert Spitzer (1939) was motivated by improving classroom performance. He opted for the worst case of heterogeneity. While I struggled with pages of mixed difficulty material, and Ebbinghaus struggled with meaningless material, Spitzer compounded those effects by the heterogeneity of minds. Instead of pages of questions, Spitzer had groups of pupils exposed to pages of reading materials. In those noisy conditions, it is hard to see the regularities of exponential forgetting and spaced repetition. Even if Spitzer’s results were overwhelmingly positive, I doubt the bureaucracy of the education system would make a good use of the procedure. Education is driven by standardized testing, grades, and certificates. It is hardly ever driven by science and the actual impact of the learning procedure on learning outcomes. It is a factory system. Spitzer’s efforts were as doomed as those groundbreaking ideas of Benezet spawned a decade earlier (1929)
- Wozniak (1985). My own misleading experiment on spaced repetition started on Jan 31, 1985, and might have ruined my efforts had it sufficiently confused my mind. Luckily, before the results came in, I designed a better experiment and was never impacted by the confusion.
Ebbinghaus experiments (1885)
The myth
A popular myth says that Ebbinghaus invented spaced repetition back in 1885. That myth was born from our own SuperMemo documentation. When we compiled the history of SuperMemo for the web in 1997, we added a few names with contribution to memory research. As explained here, it was important to keep SuperMemo grounded in science. My own contribution has always been minimized because of the negligible weight of my name. As Ebbinghaus came at the top of the list for chronological reasons, it soon gave birth to the idea that he was the father of spaced repetition. Even our own materials evolved in that direction by mistake by careless editing. Today, the web is swamped with Ebbinghaus and the serrated set of forgetting curves. If you Google for the forgetting curves, you will see this:
Figure: Google search for ” forgetting curve” (November 2017). The “serrated set” of forgetting curves dominates the search. Many of the pictures are labelled by wrong attribution with the name of Hermann Ebbinghaus. The more fit origin of the picture is presented in Two components of memory
These are the same serrated curves that I depicted in Optimization of learning (1990):
Hypothetical mechanism involved in the process of optimal learning
For more on the myth see our blog: Did Ebbinghaus invent spaced repetition?
The fact
We should rather be amazed with the fact that Ebbinghaus did not come up with spaced repetition. He was very close. He was touching all the right buttons.
This is what he wrote about the spacing effect:
For the relearning of a 12-syllable series at a definite time, accordingly, 38 repetitions, distributed in a certain way over the three preceding days, had just as favorable an effect as 68 repetitions made on the day just previous. Even if one makes very great concessions to the uncertainty of numbers based on so few researches, the difference is large enough to be significant. It makes the assumption probable that with any considerable number of repetitions a suitable distribution of them over a space of time is decidedly more advantageous than the massing of them at a single time.
Why did Ebbinghaus not take the next seemingly obvious step to see how the forgetting curve changes upon review? For one, he did not test forgetting, but the saving on re-learning. His tests were a review. With my approach it is easy to want to achieve a set level of retention. It is conceptually less intuitive to ask for a set reduction in the cost of re-learning.
However, a solution to overcoming that conceptual obstacle would be to persist with learning. Creativity thrives on the investment of time and thinking in varying contexts. To me, the answer to the Ebbinghaus puzzle is very simple. Like a good scientist, Ebbinghaus was theory-perfectionist. He chose to memorize nonsense syllables to minimize interference from his prior knowledge. Unfortunately, this had a few bad side effects:
- his lists were hard to learn and his forgetting curve was very steep. It makes for a very discouraging picture for any student who cares about remembering in the long term
- his lists gave him no pleasure in learning. This is the exact opposite of what I experienced in 1985. Every item in my paper collection was a little step forward in advancing my knowledge to a new level. Once I plotted my first forgetting curve, I wanted to know what happens after the next review
- Ebbinghaus has focused on the time or effort needed for re-learning, while I always was primarily interested in retention with little interest in how much time or effort is needed to bring the recall back to 100%
I will then venture a claim that in all his heroic memorization efforts, Hermann Ebbinghaus got fed up with learning nonsense. This would break the most persistent student. My better luck came from the burning need for getting good results in learning. This resulted in self-perpetuation of the effort. This is helpful in overcoming creative obstacles.
Interestingly, in 2015, Jaap Murre reproduced the original Ebbinghaus experiment with meticulousness worth Ebbinghaus himself (even digging into original manuscripts). Murre was prudent enough not to subject himself to the mental strain of nonsense syllables, which actually might have introduced some bias. He took the best subject available: a 22-year-old student who was rewarded with co-authorship of the publication. Incidentally, Murre seems to have been able to capture the circadian effect of learning in that his curve shows a minor bump after the period of 24 hours.
Saving on re-learning
There is a huge difference between retrievability and “savings in re-learning”. Depending on the timing, no retrieval may mean that the fact has “just been forgotten, and easily re-relearned” or “forgotten for good”. Saving on re-learning may be non-zero on materials with zero retrievability. In simple terms, lack of access to memories does not imply zero stability. In that sense, Ebbinghaus curve is not even a good expression of exponential forgetting. There will be a different saving on re-learning for difficult material and for easy material.
Forgetting curve (1984)
While writing the chapter about forgetting curves, I thought that my own notion of the forgetting curve was erroneous at the beginning. However, while digging into my archives, by accident, I discovered that I had also plotted a forgetting curve for the retention of English vocabulary in 1984, just a few months before designing SuperMemo on paper:
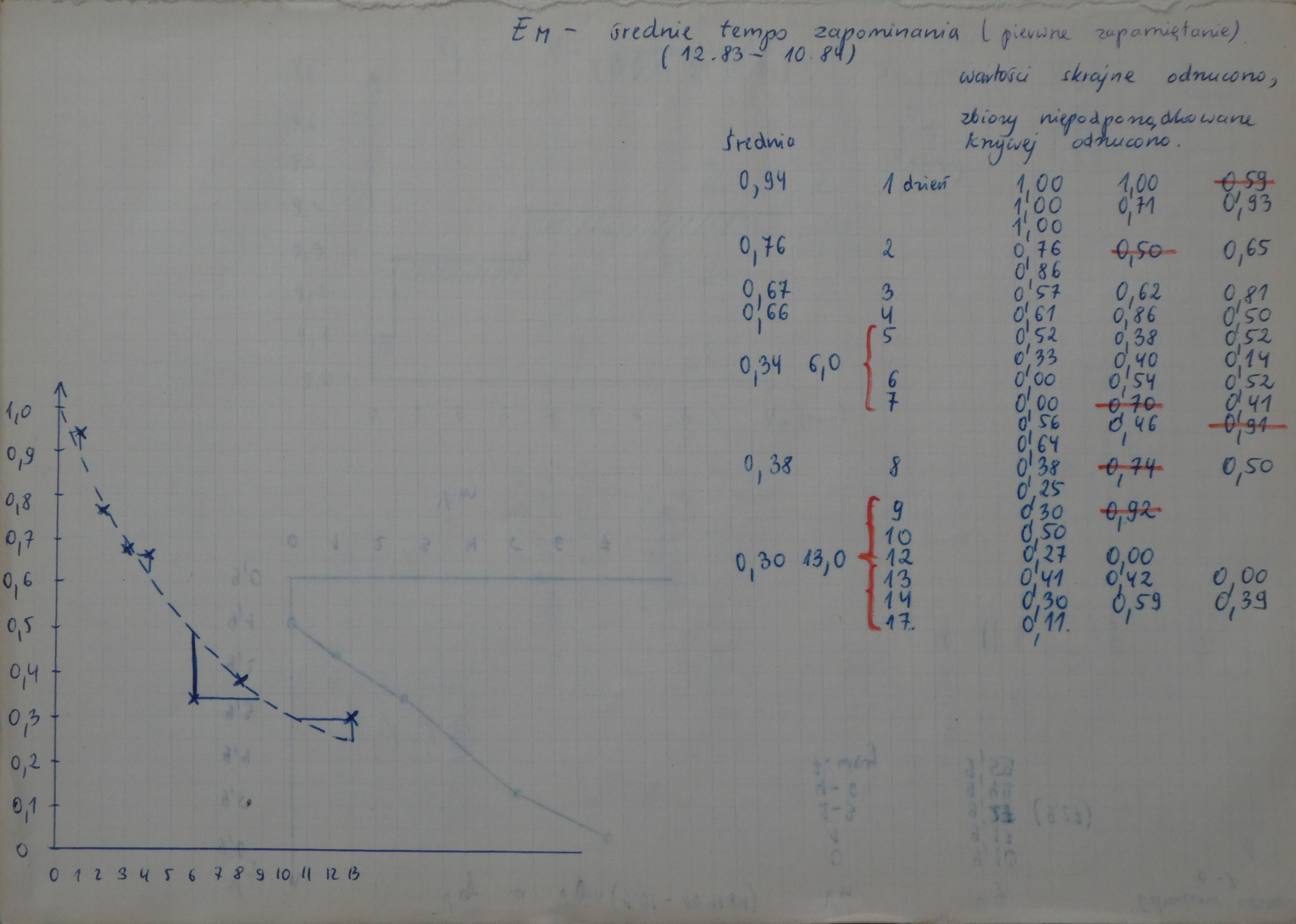
Figure: My very first forgetting curve for the retention of English vocabulary plotted back in 1984, i.e. a few months before designing SuperMemo on paper. This graph was not part of the experiment. It was simply a cumulative assessment of the results of intermittent learning of English vocabulary. The graph was soon forgotten. It was re-discovered 34 years later. After memorization, 49 pages of ~40 word pairs of English were reviewed at different intervals and the number of recall errors was recorded. After rejecting outliers and averaging, the curve appears to be far less steep that the curve obtained by Ebbinghaus (1885), in which he used nonsense syllables and a different measure of forgetting: saving on re-learning
I forgot about the fact of plotting that curve. I presume, once I had SuperMemo, that curve no longer seemed important or relevant. I was not focused on the “science of memory”. I just wanted to get good results in learning. Apparently, I did not think that plotting a forgetting curve was a big deal. I nearly missed that figure in 2018 too as it was labelled in small print: average speed of forgetting for the first memorization.
The result came from 49 pages of 40-word pairs each, i.e. 1960 words (compare: 13 years of school in a month). I did all my learning for learning’s sake, not for the experiment. There was no experiment actually. All I needed was to collect the numbers from my actual learning effort and plot the curve. The simplicity of the calculation might also explain why I forgot the exercise so easily.
I wrote about simple intuitions before the 1985 experiment. In the light of this 1984 curve, it might seem that the intuitions may have been derived from that little experiment. What today seems obvious might not be that obvious without the crutch of that little calculation. However, I can guess that by Feb 1985, I have already forgotten my curve because I did not skip Stage A in the spaced repetition experiment. My forgetting curve agreed with the experiment and the first review interval should be 1 day indeed.
The erroneous notion of sigmoidal curves must have been born later. Today, I seem to recall remotely that I originally thought that the sigmoidal nature kicks in only after the first review. I might never know how my thought process worked at that time. All I cared was the efficiency of SuperMemo. In the excitement of the discovery of SuperMemo, I forgot my curve for the entire 34 years. Today, that little graph matters only to illustrate how easily we can discover, forget, stray, re-discover, and then re-discover the original discovery. Memory is fallible. God bless spaced repetition.
Figure: The very first forgetting curve for the retention of English vocabulary plotted back in 1984 (a few months before designing SuperMemo on paper). This graph was not part of an experiment. It was simply a cumulative assessment of the results of intermittent learning of English vocabulary. The graph was forgotten and re-discovered 34 years later. After memorization, 49 pages of ~40 word pairs of English were reviewed at different intervals and the number of recall errors was recorded. White circles correspond with recall derived from the average number of errors per page after a given interval. Logarithmic regression in orange provides the best fit. Power regression in red follows closely. This could be expected from heterogeneous material (pages of words). This is also very similar to the results obtained by Ebbinghaus (1885), except the curve is far less steep as befits meaningful material. As expected, exponential regression in white provides the weakest fit
Spitzer experiment (1939)
In 1939, Herbert F. Spitzer investigated various testing schedules on 3605 sixth-grade pupils in 9 Iowa cities. This was the entire population of 91 schools. The kids read a 6-page text and their knowledge was later tested with 25 specific questions.
Spitzer designed different testing schedules, however, the design clearly did not aim at optimum spacing, and his research summary did not make any recommendation in that respect.
Figure: Diagram of procedure. Spitzer (1939).
Only the first two groups of students used an expanding schedule. These were the groups that came top on tests, however, Spitzer attributed this to the testing effect as these were the only two groups with 3 tests, i.e. the middle test was interpreted as a “testing intervention” (rather than repetition).
Figure Spitzer (1939). Curves of retention
In his recommendations, Spitzer focused on the power of the testing effect, of what I call “active recall” in reference to my flashcards of 1982. What I like about his paper is the recommendation that testing be used for students to correct their own knowledge, provide feedback, and thus give them a sense of their progress. This stands in contrast to modern testing that is more often used as a whip to push kids to do more learning.
Spitzer’s diagram of intervals reminds me of my own self-administered test that failed to produce convincing results. In this case, intervals are clearly clocked by school life, not by demands of memory.
In his research, Spitzer exhibited ruthless Gatesian approach to testing and learning, typical of early school innovators that often did more damage than good by being too thorough! Educators who do not employ the learn drive in the process, are doomed to fail even if they employ the best tools for boosting memory!
I cannot but remark on the issue of ethical considerations. While we slaughter millions of animals in the name of science, we might perhaps fail to notice that this research, with all the best intent at heart, used the labor of 3000+ involuntary participants. What is great for memory research does not need to be great for individual learning. In the era of Google, I found the test texts used by Spitzer pretty offputting. Despite the fact that a great deal of effort was put into the selection of the subject matter and wording, I would consider coercive reading a violation of my freedom. Those materials might be much better than your school average, but schooling will always be about mass production and less about creative freedom.
Reading about a biology of banana plants might be palatable to a gardener or a biologist, which I claim to be. However, why would kids need to read about bananas if their current interest was the Great Depression, the Dust Bowl, Nazi Germany, or baseball?
School is the time when we stop learning and start cramming. It is the time when we lose the love of learning. Adding spaced repetition to this coercive mix could only make things worse.
Wozniak experiment (1985)
Before I managed to compute optimal intervals for reviewing pages with English vocabulary, I designed an experiment which might have put me on wrong tracks. The experiment was to show the value of the progressive increase in review intervals. Instead, it showed that equally spaced review might be superior.
Experiments in science should not be considered “failed” just because they come with unexpected results. However, in this case, unexpected results came from bad design, and might have resulted in confusion that would inhibit further progress. To this day researchers speak of “mixed results” in spaced repetition due to wrong design or even simple terminological confusion.
Fortunately, my intuitions about memory in 1985 were too solid, and it was pretty obvious that with rapid acceleration in the expanding length of intervals, forgetting might overwhelm consolidation. My progressive schedule was simply not optimum. I would have certainly designed a better follow-up. Most of all, I wanted to continue learning with success. I doubt I would have given up without a good solution.
The experiment shows that it is not enough to have a good guess about what optimum intervals are. The intervals actually need to be computed.
Archive warning: Why use literal archives?
This text is part of: ” Optimization of learning ” by Piotr Wozniak (1990)
At the beginning of 1985, I designed two experiments which consequently revolutionized my learning methodology and led to the formulation of the SuperMemo method.
The first experiment can be a good illustration of how a misconceived idea can yield valuable conclusions (the second is described here). It is a common intuition that with successive repetitions, knowledge should gradually become more durable and require less frequent review. Thus repetitions separated by increasing intervals should be more effective than those whose intervals are always the same. This belief proved to be false. Let us see an experiment which demonstrates the fact:
Experiment on the influence of various repetition spacing patterns on the effect of repetitions on knowledge retention (Jan 31, 1985 – Aug 2, 1986)
- The memorized knowledge consisted of 195 items divided into three equal groups: A, B and C.
- Each of the items had the following form:Question: English irregular verbAnswer: simple present, simple past and past participle forms of the verb in question
- All items of a particular group were memorized in one session by repeating them until all were known (group A – Jan 31, B – Feb 2, C – Feb 3).
- Two final control dates were established: Dec 6-7, 1985 and Aug 1-2, 1986 on which the level of retention in all groups was measured at the same time (for each item the accuracy of recall was measured in a four grade scale).
- Before the control dates, all of the groups A, B and C underwent 6 independent repetitions in the following intervals (expressed in days):
| Repetition number | Group A (equal spacing over a longer time) | Group B (spacing based on increasing intervals) | Group C (equal spacing in 30 days) |
|---|---|---|---|
| 1 | 18 days | 1 day | 5 days |
| 2 | 18 days | 5 days | 5 days |
| 3 | 18 days | 9 days | 5 days |
| 4 | 18 days | 24 days | 5 days |
| 5 | 18 days | 44 days | 5 days |
| 6 | 18 days | 70 days | 5 days |
The intent of the experiment was to prove that increasing intervals are the best for memory consolidation (group B) as opposed to intervals that are evenly distributed (group A) or concentrated in time (group C). The results of the experiment are shown in Fig. 3.1:
The results of the second control are not present on the graph because of the prosaic fact that studying at the University of Technology [started in October 1985] required perfect knowledge of irregular verbs, therefore another measurement was pointless.As it can be seen in Fig.3.1 above, the experiment yielded unexpected results proving that increasing inter-repetition intervals need not be better than constant-length intervals. Fortunately, long before the results of the experiment were known, I suspected that there must exist optimum inter-repetition intervals. The principle of using such intervals in the process of learning will be later be referred to as the optimum repetition spacing principle.
While writing History of spaced repetition, I found the original graphs in my archive. It is pretty obvious that massed practice is not a good approach:
| Group A: distributed spacing in 18 day intervals | Group B: spacing based on increasing intervals | Group C: massed spacing in 5 day intervals |
|---|
Why spaced repetition idea succeeded in the end?
Spaced repetition is intuitive. After some reflection, it is even obvious. Why didn’t we come up with solutions earlier? SuperMemo on paper would be feasible as soon as mankind came up with paper. However, in ancient times, the volume of vital knowledge was small enough for the brain to easily cope with the deployment of natural learning methods. By working in the field, the farmer quickly gains all necessary expertise that helps him excel for as long as health permits.
Things started changing with the arrival of print in the 15th century. Knowledge started proliferating and it also gained means of efficient perpetuation. Newton at plague years might be an interesting example of an individual who would theoretically benefit from spaced repetition. However, Newton’s book collection was limited and the problems to think about and solve were so numerous that it is easy to imagine he would never be bothered with his failing memory. All he needed was to make notes.
Over the next two centuries, the stores of available knowledge kept increasing and human natural appetite for remembering might have been increasing at the same time. Research by Ebbinghaus in the 1880s is an example of a continual interest in the workings of memory. However, even today, most of the scientists are rarely bothered by their forgetting. Making notes and Google can satisfy most of the needs for most of them. When Vannevar Bush conceived memex device in the 1930s, he saw it as a memory augmentation. However, even if memex was to be seen as a distant cousin of incremental reading or neural creativity, all its knowledge, like in Google, lived predominantly outside of the human brain. My quest reminds me that of V. Bush except I want to see all that knowledge make a direct imprint on human creativity (see: neural creativity).
Why was I particularly bothered by forgetting? There are many kids out there who like to show off at school. When my brother showed me how to differentiate needles of a spruce and a fir, in my 3rd-grade biology class, I was eager to show that I know more than your average kid. That eagerness was quickly suppressed by schooling, but some traces survived. When we started learning chemistry in Grade 7, I was proud to be able to recall complex names like adenosine triphosphate or deoxyribonucleic acid. I was even looking up difficult chemistry names to memorize and impress. I memorized the details of the anatomy of a jawless fish. Again I tried to impress at school, but no one was interested.
When I got deeper into zoology in Grade 5, some kind of OCD for information started showing up. I wanted to know all animals in the Poznan zoo, their habitat, and even their taxonomy and Latin names. I got fantastic books with photographs of all animals and knowing them seemed like an interesting endeavour.
In 1974, I became interested in boxing, football, and sports in general. I used to visit the waste paper store in our school and search for sports journals. My colleague Robert asked me to collect pictures with naked ladies. I complied. My puberty was late and I was not interested. When the stack of photos spilled at home, I explained it to my mom ” not for me!“. She nodded compassionately with a smirk. In the meantime, I would use an iron to remove wrinkles from my recycled sports journal collection. I would stack them up neatly and archive by date. The stack filled up several shelves in bookcases in my room. That obsessive neatness would make for a disturbing picture for any parent, however, my mom was tolerant. I was free to follow my passions even if they seemed preposterous. I have no doubt that freedom is one of the vital ingredients of healthy development. Don’t many kids show similar symptoms in obsessions with stamp collecting, postcards and football cards?
Some early drive in the direction of incremental reading showed some time between ages 10 and 12. I started making notes about horses by following links in a paper encyclopedia. It was fun to start with one entry, and hope to write a booklet about horses by just following the links. In Grade 1 of high school (aged 12), I did a similar exercise with an encyclopedia of mammals. There was some inner need to codify all information about certain subjects in biology. I decided to write an encyclopedia-sized book about the living world. I used a typewriter at mom’s work and my own rich illustrations to write the history of evolution. I never finished. The futility of that exercise should be obvious. It never bothered my mind. The effort was enjoyable and addictive.
I showed a similar informavorous nature when I started learning zoology, chemistry, biology, and later biochemistry during summer vacations 1977-1979 (aged 13-15). This was a definite start of my growing need for remembering. I would produce calligraphically written and meticulously illustrated books with my newly acquired knowledge. However, after a longer while that knowledge tended to evaporate. That futility started bothering me slowly. What’s the point of writing books if soon they turn into the same dead material like all other books on the shelf?
Around the year 1981-1982 (aged 19-20), I started writing down my knowledge in the form of questions and answers for active recall tests. I knew that this was the only way to preserve things in memory for longer. Needless to say, after a while, the chaotic review did not provide full satisfaction either. At that stage, I was clearly very hungry for knowledge. I wanted to remember. Simple intuitions led to simple experiments and then to a simple SuperMemo for DOS. I was driven by practical applications that combined research with the pleasure of learning.
As of that point, my path has become deterministic. I loved learning too much to give up SuperMemo in difficult times. My love of learning was easily suppressed at school or when I was involved in running a business. However, once I decided to work from home (1997), the positive feedback loop has set in between learning, love of learning, and the progress of SuperMemo. As this also happens to be the way to earn a living, that loop is for ever. Only bad health or death can break this cycle. That part of the formula for progress is easy to figure out.
What could parents do to facilitate similar passions in kids? I think two ingredients come into play: inspiration and freedom. While inspiration is helpful, freedom is essential. These days, inspiration can be found all around. YouTube plays a huge role where humans don’t live up to the mark. All around the world, it is the freedom ingredient that is missing most. Kids are enslaved by schooling. They are also enslaved by authoritarian parenting. I was told many times that some of my crazy behaviors are a side effect of growing up without a father. This might be true. However, to compensate, I had three parents. Mom and two older siblings: inspiring brother and a childless sister who channeled all her love into the little brat of me. I venture a claim that I came to this world with a reasonable endowment, not much above the average. I often lingered at the bottom of the class. Rarely would I come to the lead. I have dozens of examples when I converted meager skills or a bit of talent into excellence in a narrow area of creative pursuits. Freedom and rage to master were always the key ingredients. When I bread dozens of animals or collected dead body parts, my family might ask ” why is the kid not going to church instead?“. My mom would shield me from those influences and concerns. I could do things my own way.
My development was then primarily boosted by the impact of freedom. Freedom helps the learn drive thrive, and the learn drive has self-amplifying powers. This led me to obsessions that make it possible to boast today of fathering spaced repetition. Passions and obsessions should be cherished. Instead, we tend to exterminate them in the name of robotization of development. We set benchmarks and ask kids to jump through the hoops. As if being led by the hand through college has ever contributed to anyone’s independent thinking. This decorticating process needs to stop! The future belongs to free learning.
As for spaced repetition, the appetite for solving the problem of forgetting increased substantially with the arrival of personal computers. In the early 1990s, I heard it with increasing frequency from users of SuperMemo that they thought of a similar solution for themselves but decided to look around for a specific software application first.
It is the demands of school that cause most frustrations in students today, however, schools are not a good place for creative thinking. Students do flock to spaced repetition mostly because it is served on a silver platter. It is ready to consume. Very few contemplate their own solutions.
In addition to personal freedoms, some of the good fortunes that gave a good start to SuperMemo were: (1) free university in communist Poland, (2) family sponsorship in purchasing an outrageously expensive PC, (3) lenient schools that did not impose much on my free time, etc.
You will not see many 22-24 year olds tinkering with their own science at the cost of the state or their family. There is nothing wrong with young adults living with their parents if they pursue creative goals.
Spaced repetition was born at the confluence of good forces: free learning in a communist system, the transition from communism to the market economy, and the arrival of personal computing. That was boosted by freedom at home and a dose of healthy obsession with learning. The main ingredient of that equation is freedom. Freedom is replicable. All it needs is to be granted.
First decade of SuperMemo: Battling skepticism
Skepticism surrounded the early days of SuperMemo in Poland. This was expressed pretty accurately in the Polish computer journal Enter in 1994 (see full article):
SuperMemo might work but it cannot be that good
If one is convinced of the validity of what has been said about SuperMemo, will he or she be already convinced that the program is a perfect cure for the ailing memory? Can it really capitalize on the properties of the nervous system and let learning proceed a dozen times faster than in standard circumstances? After all there have been generations of students trying to figure out better methods of learning, and a breakthrough comparable with SuperMemo seems highly unlikely even to quite an open-minded observer. Wozniak discounts the low-probability argument as the viable source of skepticism, and says that he has more than once traced down evidence that SuperMemo-like approaches to learning have already been tried before with lesser or greater degree of success. Moreover, it is worth noticing that SuperMemo might not see the light were it not implemented as a computer program which can easily be transferred between individuals. In other words, it could have fallen into oblivion as the previous attempts to put order in the process of learning. One must remember that the skeletal algorithm of SuperMemo has been formulated in 1985, and only 1987 saw its very slow expansion in selected scientific circles in Poznan. Another turning- point to be kept in view is that SuperMemo World would not have been formed in 1991 were it not for the inspiring meeting of minds between Wozniak and his colleague from the university, Krzysztof Biedalak, currently SuperMemo World’s Vice-President. Both top-students at the university, Wozniak intended to study neuroscience in the US, Biedalak wanted to do the same in the field of artificial intelligence. Only by coincidence, they were both thrown into the world of entrepreneurial science. All this shows that despite the fact that the principles of SuperMemo are extremely simple and might have been invented several dozen times independently in several dozen countries of the planet, SuperMemo is not just a run-of-the-mill. The distinctive merit of SuperMemo World was to put the idea in practice, invest a great deal of man-hours in the development of the software, and focus on marketing the idea to the potential customer. Otherwise, SuperMemo would have forever remained limited to the small circle of its early enthusiasts.
The future is bright
I mentioned that the progress of spaced repetition has been bogged down by guesswork, weak practical toolset, and terminological confusion. Today, all those factors fall by the roadside. New web applications come into force, they combine big data, and practical needs of users. They all use the same terminology: forgetting curve, spacing effect, and spaced repetition. The future of learning looks brighter than ever.



