- 하루 15분 동안 언어를 학습하며 빠르게 실력을 향상시키세요.
- 전 세계적으로 인정받은 SuperMemo의 지능형 반복 학습법으로 어휘와 표현을 영구적으로 기억하세요.
- 25개 언어와 300개 가까운 코스에 액세스할 수 있습니다.
- AI 기술을 활용한 MemoChat에서 실제 대화를 연습하며 말하기 실력을 향상시키세요.
- 온라인 또는 오프라인으로 원하는 만큼의 기기에서 앱을 사용하세요.
당신은 어떤 언어를 배우고 싶습니까?
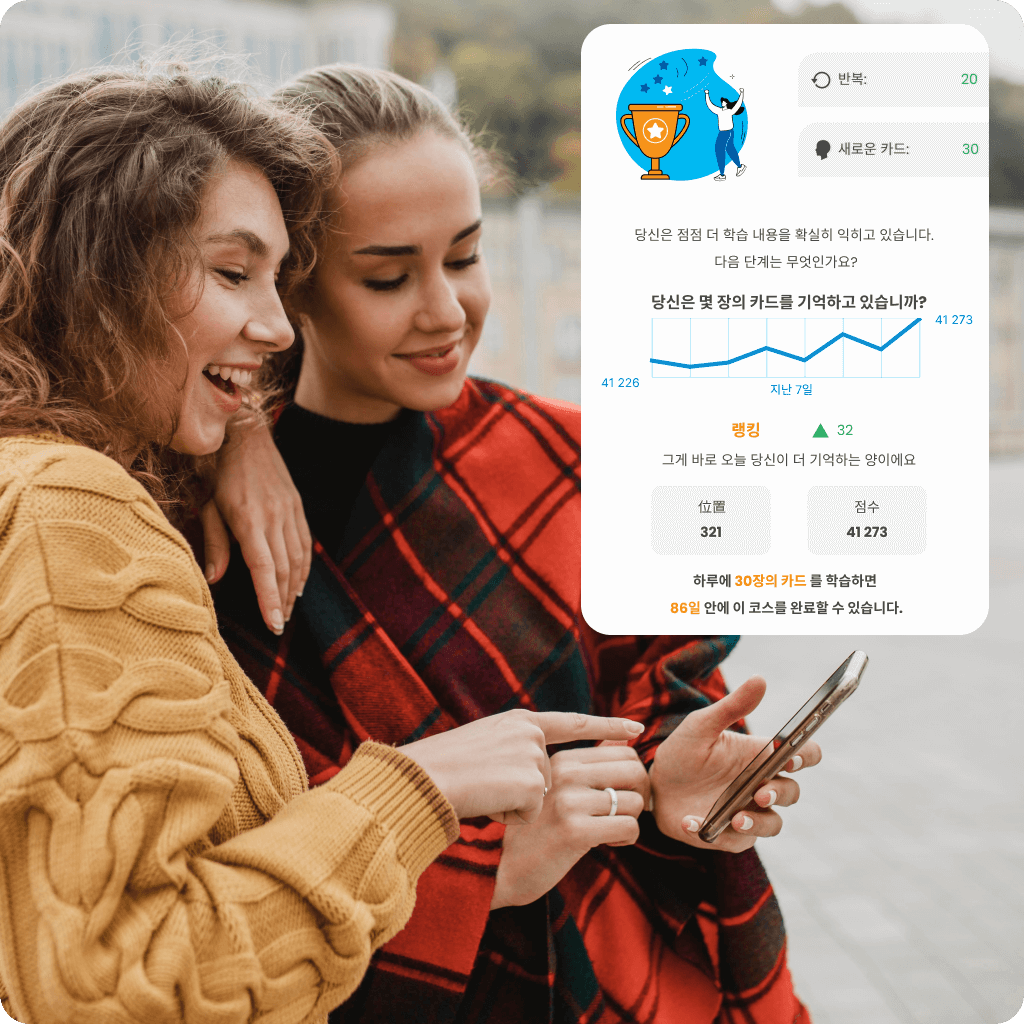
우리는 효과적인 온라인 학습을 지원하기 위해 지능형 반복 시스템을 처음 도입한 선구자입니다. 독창적인 연구와 개발을 통해 이 기술 분야에서 리더로 자리매김했습니다.
제공하는 모든 온라인 언어 코스는 복습의 이상적인 시점을 정확히 결정하는 독점 알고리즘에 기반합니다. 이를 통해 더 빠르고 효과적으로 학습하며, 지식을 오랜 기간 기억할 수 있습니다.
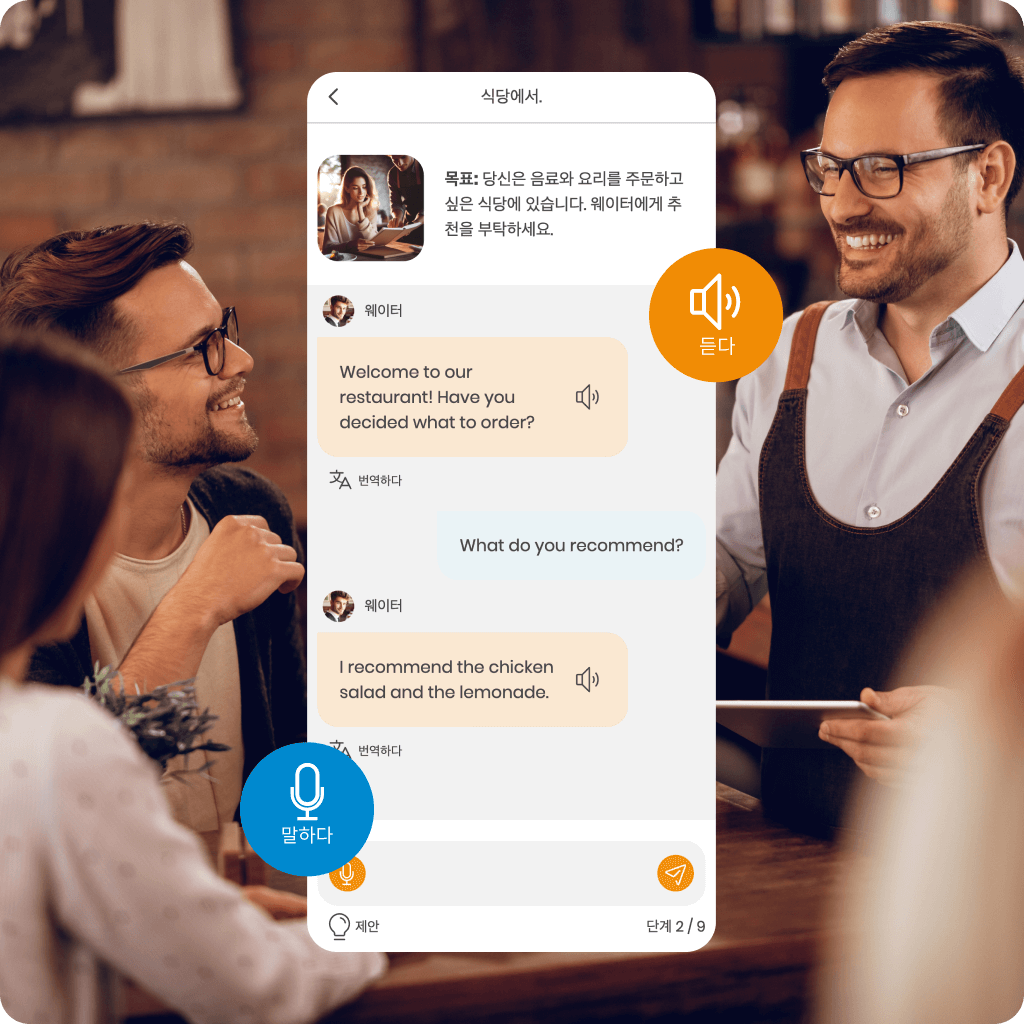
MemoChat을 발견하세요 – SuperMemo의 AI 기술로 구동되는 인터랙티브 대화 기능으로, 다양한 대화 주제를 제공하며, 사용자가 직접 주제를 제안할 수도 있습니다. MemoChat은 응답 제안, 즉시 번역, 오류 수정 기능을 제공하며, 새로 배운 단어를 쉽게 코스에 추가하여 개인 맞춤형 학습 자료를 만들 수 있습니다。
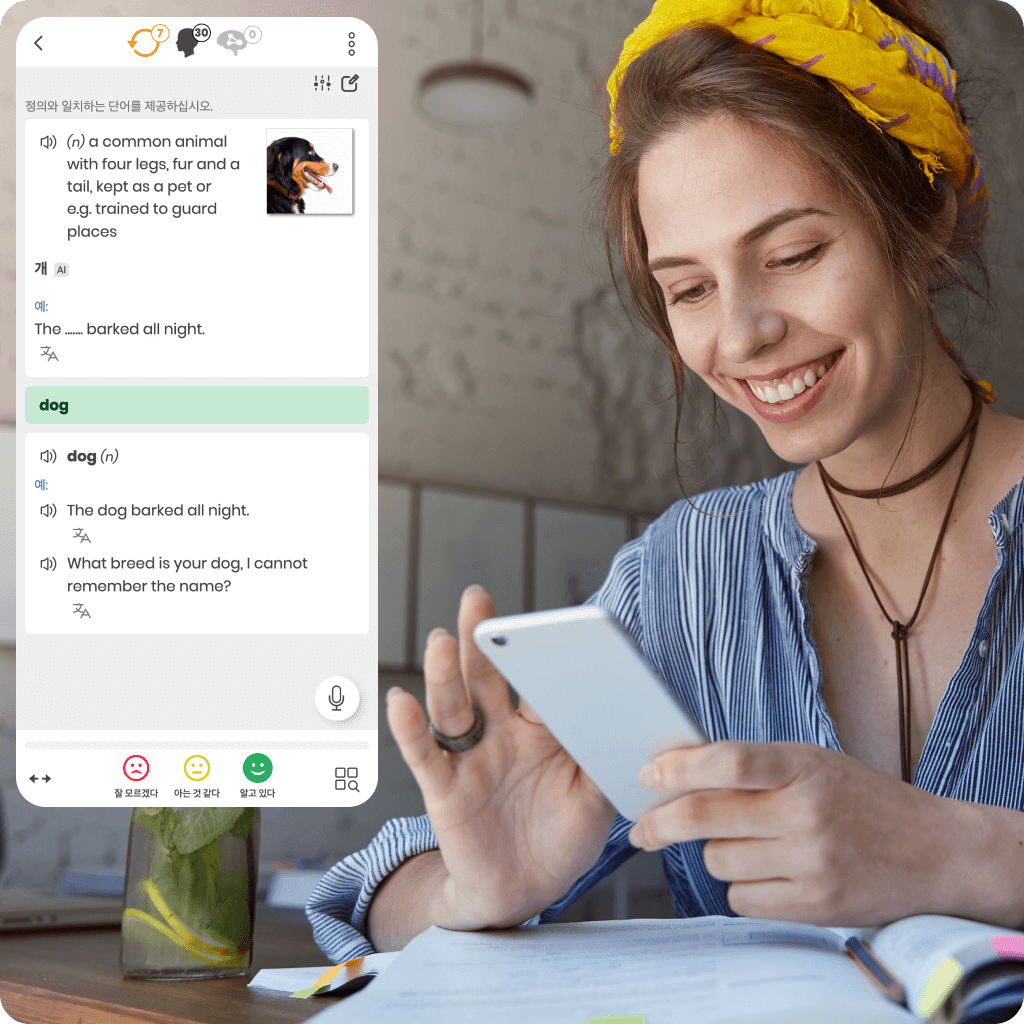
AI 어시스턴트의 도움으로 문법을 이해하고, 익숙하지 않은 단어를 번역하며, 이를 문맥에 맞게 올바르게 사용하는 방법을 배울 수 있습니다. 이를 통해 학습 진도가 크게 향상됩니다。
추가적으로, MemoTranslator는 단어와 문장을 즉시 번역하며, 이를 코스에 추가하여 학습을 더욱 효과적으로 만들 수 있습니다。

어휘와 문법을 모든 숙련도 수준에서 발전시키는 다양한 코스를 탐색하세요. 음성 인식 기능과 인터랙티브한 대화를 통해 말하기 자신감을 키우세요. 읽기 이해 능력을 향상시키고 철자법을 완벽히 다듬어 보세요.
앞으로 학습할 내용을 전부 기억하고 싶으세요? 이 알고리즘에 맡겨 보세요.
Gary Wolf, WIRED