- Impara una lingua per 15 minuti al giorno e fai progressi rapidi.
- Memorizza in modo permanente il vocabolario e le espressioni con il metodo di ripetizione intelligente di SuperMemo, riconosciuto a livello globale.
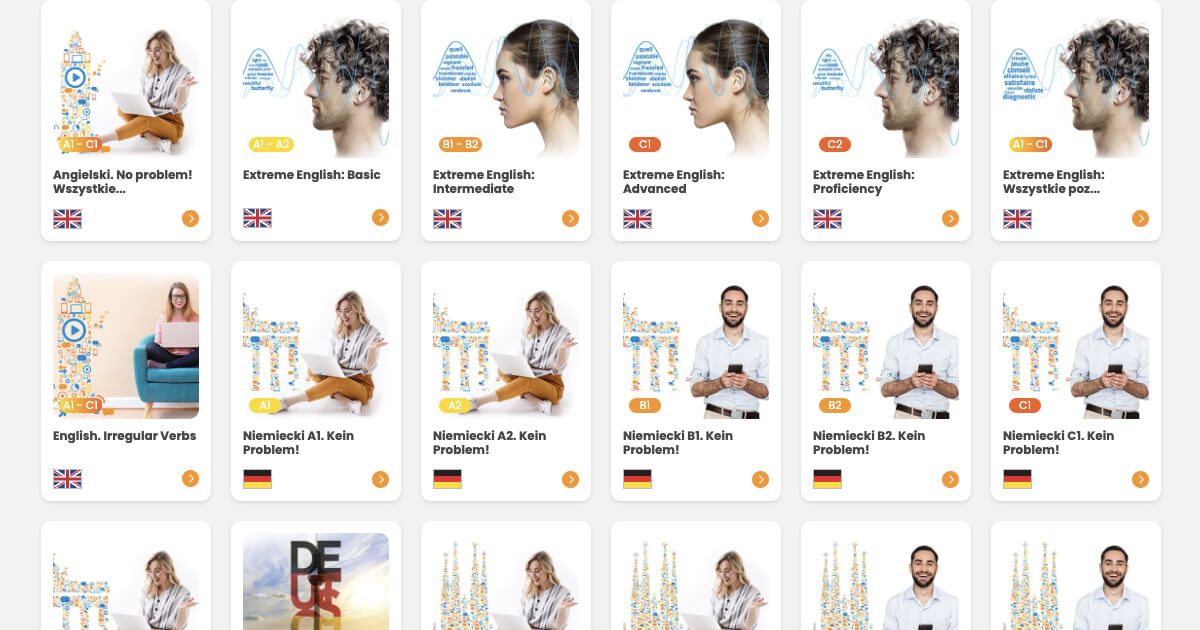
- Accedi a 25 lingue e a quasi 300 corsi.
- Sviluppa le tue abilità di conversazione praticando dialoghi reali in MemoChat con la tecnologia AI.
- Usa l’app su un numero illimitato di dispositivi, online o offline.
Quale lingua desideri imparare?
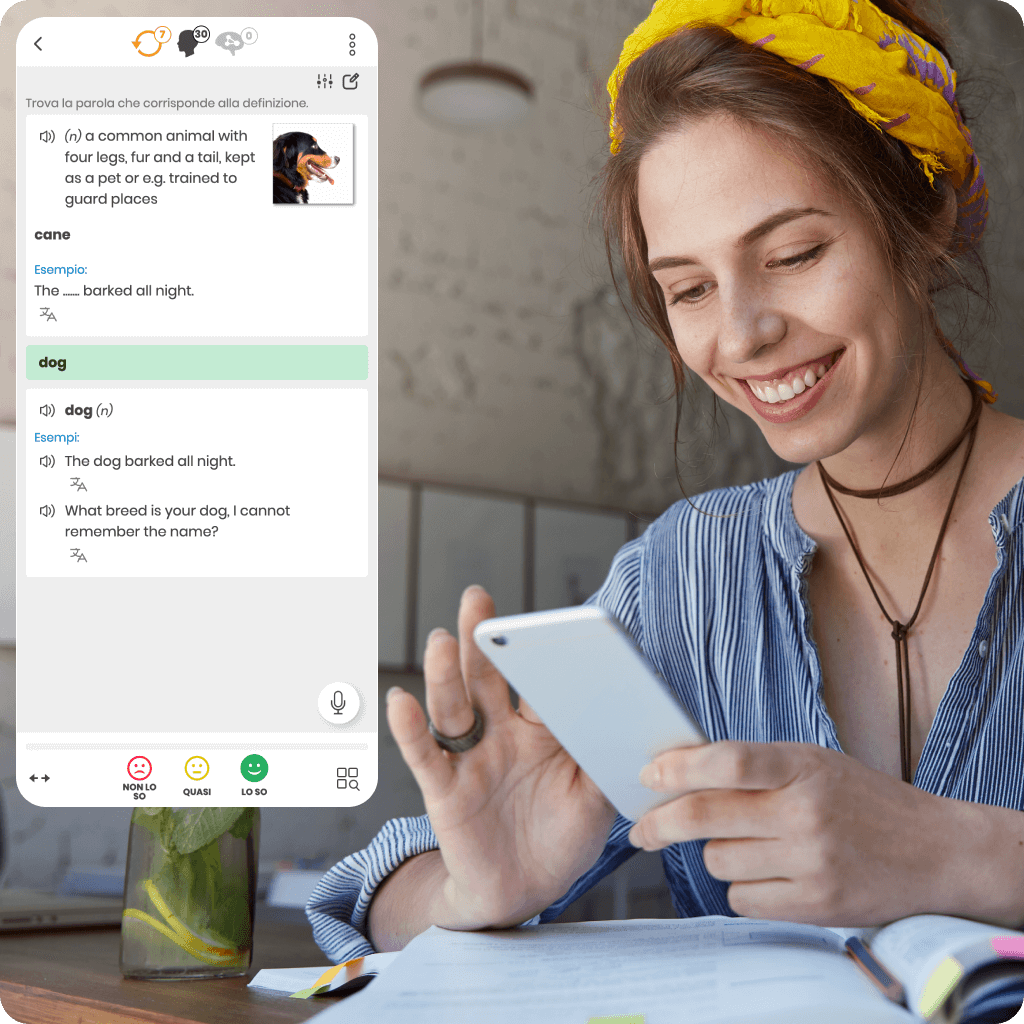
Siamo stati i primi a introdurre il sistema di ripetizione intelligente per supportare l’apprendimento online efficace. La nostra ricerca e sviluppo unici ci rendono leader in questa tecnologia.
Ogni corso di lingua online che offriamo si basa su un algoritmo proprietario che determina con precisione il momento ideale per le ripetizioni. Questo garantisce un apprendimento più veloce, più efficace e una conoscenza duratura.
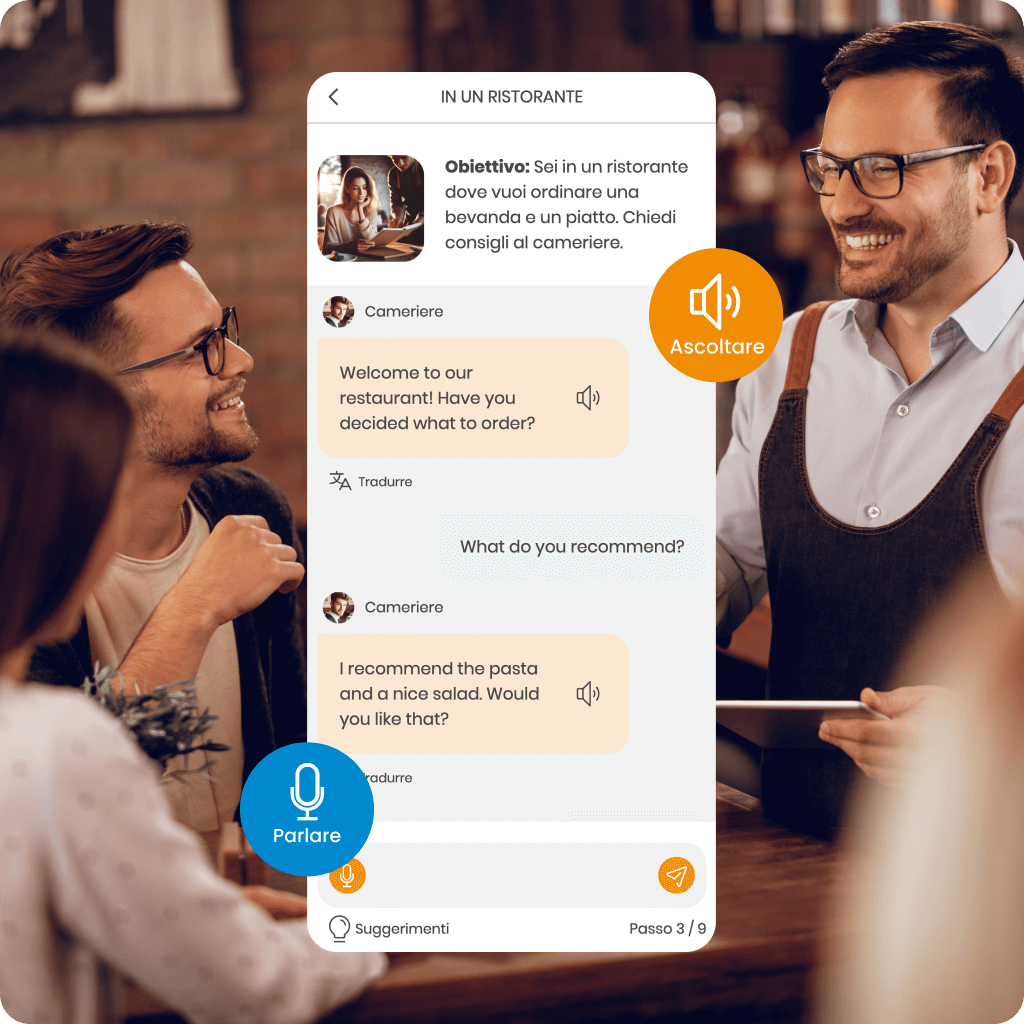
Scopri MemoChat – dialoghi interattivi in SuperMemo alimentati dall’IA, che offrono una varietà di argomenti di conversazione e la possibilità di proporre i tuoi. MemoChat fornisce suggerimenti di risposta, traduzioni istantanee e correzioni degli errori, mentre le parole appena apprese possono essere facilmente aggiunte ai tuoi corsi, creando materiali di studio personalizzati.
Con l’aiuto del Assistente AI, comprenderai la grammatica, tradurrai parole sconosciute e imparerai a usarle correttamente nel contesto, accelerando significativamente i tuoi progressi.
Inoltre, il MemoTranslator traduce istantaneamente parole e frasi, che puoi anche aggiungere ai tuoi corsi per rendere l’apprendimento ancora più efficace.
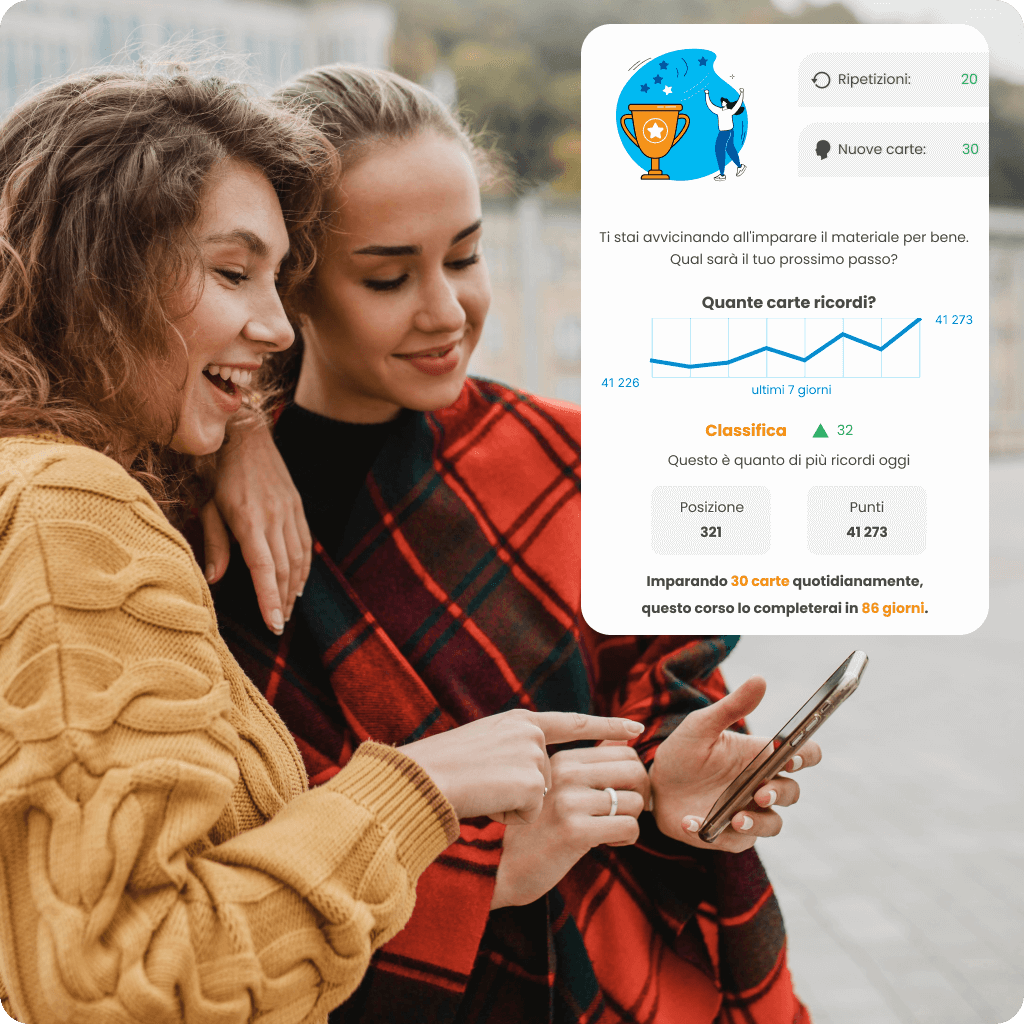
Adatta il tuo ritmo di apprendimento delle lingue alle tue esigenze e al tempo disponibile con un piano di apprendimento personalizzato. Monitora i tuoi progressi in tempo reale con le statistiche, verifica quanto hai già imparato e guarda la tua posizione nella classifica rispetto agli altri utenti. Scegli un corso che non solo ti motiva ad agire, ma ti aiuta anche a raggiungere i tuoi obiettivi in modo efficace.

Esplora una varietà di corsi che sviluppano il vocabolario e la grammatica a tutti i livelli di competenza. Acquisisci sicurezza nel parlare con la funzione di riconoscimento vocale e dialoghi interattivi. Migliora le tue abilità di comprensione del testo e perfeziona la tua ortografia.
Vuoi ricordare tutto quello che hai appreso? Segui questo algoritmo.
Gary Wolf, WIRED